
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ортогональное преобразование
|
|
|
|
Уже в аналитической геометрии на плоскости приходится встречаться с поворотом направленных отрезков, исходящих из начала прямоугольной системы, на один и тот же угол вокруг начала и с отражением, т. е. изменением направления всех таких отрезков. Характерной особенностью этих преобразований является то, что они оставляют неизменным длину направленного отрезка. Здесь мы рассмотрим более общее понятие, а именно ортогональное преобразование евклидова пространства.
Линейное преобразование  евклидова пространства
евклидова пространства 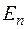 называется ортогональным, если оно не изменяет скалярный квадрат
называется ортогональным, если оно не изменяет скалярный квадрат  любого вектора
любого вектора 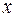 :
: 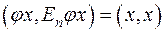 .
.
Теорема 1. Линейное преобразование  евклидова пространства
евклидова пространства 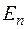 ортогонально тогда и только тогда, когда оно не изменяет скалярное произведение
ортогонально тогда и только тогда, когда оно не изменяет скалярное произведение  любой пары векторов
любой пары векторов 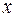 ,
,  :
:  .
.
Таким образом, ортогональное преобразование  можно определить как такое линейное преобразование пространства
можно определить как такое линейное преобразование пространства 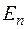 , которое оставляет неизменным скалярное произведение
, которое оставляет неизменным скалярное произведение  .
.
Доказательство. Если линейное преобразование  не изменяет скалярное произведение
не изменяет скалярное произведение  , то, полагая в равенстве
, то, полагая в равенстве  вектор
вектор 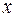 равным вектору
равным вектору  , получаем:
, получаем: 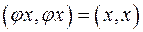 , т. е.
, т. е.  − ортогональное преобразование.
− ортогональное преобразование.
Обратно, если  − ортогональное преобразование, то
− ортогональное преобразование, то
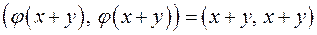 .
.
Но
 ,
,
так как 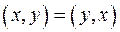 , и
, и

так как 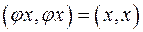 ,
,  и
и
 .Следовательно,
.Следовательно,
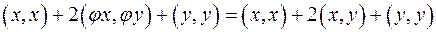 ,
,
откуда  , т. е. преобразование
, т. е. преобразование  не изменяет скалярное произведение
не изменяет скалярное произведение  .
.
Ортогональное преобразование можно определить иначе. А именно:
Теорема 2. Ортогональное преобразование  переводит ортонормированный базис евклидова пространства
переводит ортонормированный базис евклидова пространства 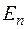 в ортонормированный базис. Обратно, линейное преобразование
в ортонормированный базис. Обратно, линейное преобразование  пространства
пространства 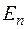 , переводящее ортонормированный базис в ортонормированный базис, является ортогональным.
, переводящее ортонормированный базис в ортонормированный базис, является ортогональным.
Доказательство. Пусть 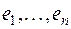 − ортонормированный базис
− ортонормированный базис 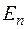 , и преобразование
, и преобразование  ортогонально. Рассмотрим систему образов
ортогонально. Рассмотрим систему образов 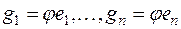 векторов базиса. Так как
векторов базиса. Так как 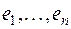 − ортонормированный базис, то в силу ортогональности
− ортонормированный базис, то в силу ортогональности 
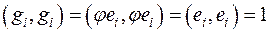 ,
,
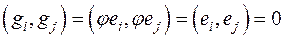 при
при  .
.
Мы видим, что  − ортонормированная (и тем самым линейно независимая) система
− ортонормированная (и тем самым линейно независимая) система 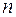 векторов, т. е. ортонормированный базис.
векторов, т. е. ортонормированный базис.
Обратно, пусть  − линейное преобразование пространства
− линейное преобразование пространства 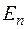 , для которого система образов
, для которого система образов 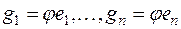 векторов ортонормированного базиса
векторов ортонормированного базиса 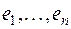 также является ортонормированным базисом:
также является ортонормированным базисом: 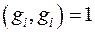 ,
, 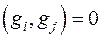 при
при  ,
, 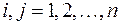 .
.
Возьмем произвольный вектор 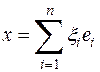 . Так как
. Так как 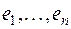 − ортонормированный базис, то
− ортонормированный базис, то  . Образ
. Образ 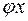 вектора
вектора 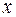 равен:
равен:
 .
.
Отсюда в ортонормированном базисе 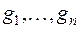
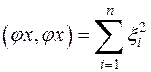 ,
,
и мы видим, что 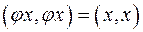 ), т.е.
), т.е. 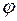 − ортогональное преобразование.
− ортогональное преобразование.
|
|
|
|
|
Дата добавления: 2015-05-29; Просмотров: 827; Нарушение авторских прав?; Мы поможем в написании вашей работы!