Теоретические основы решения

Условие задачи

ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ В ПЛОСКОЙ РАМЕ

Определение диаметра вала

Сопоставляя эпюры изгибающих и крутящих моментов, за опасное принимаем сечение С, в котором кН∙м и кН∙м.

Подсчитаем эквивалентный момент по ІV (энергетической) теории прочности, необходимый для условия прочности (6.3):

Теперь, используя условие прочности (6.3), вычислим требуемый диаметр:

Принимаем ближайшее стандартное значение диаметра вала d = 55 мм.

Таблица 6.1.Схемы к задаче 6

Таблица 6.1.Схемы к задаче 6 (окончание)

 

Таблица 6.2. Исходные значения к задаче 6

Номер варианта	Мощность N, кВт	Угловая скорость ω, 1/с	Длина l, мм	Диаметр D 1, мм

Задача 7.

Для плоской стальной рамы, схемы которой приведены в табл. 7.1, построить эпюры внутренних усилий, значение силы и длины стержней даны в табл. 7.2.

Рамой называют конструкцию, которая состоит из жёстко соединённых стержней (рис. 7.1). Чаще соединение выполняют под прямым углом, a размеры сечения всех стержней одинаковы. Нужно заметить, что стержни могут быть и прямолинейными, и криволинейными. Здесь рассмотрим плоскую раму с прямолинейными стержнями.

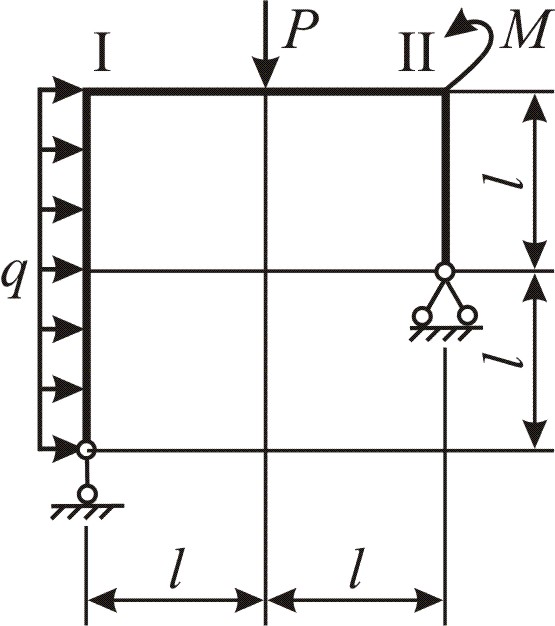Рис. 7.1

Стержень рамы может быть нагружен распределённой нагрузкой, со­средоточенными силами и моментами. Если эта нагрузка лежит в плоскости рамы, то имеем плоскую раму. В своей плоскости рама должна иметь опоры. На схеме рамы изображают заделку, если опора препятствует линейным и угловым перемещениям. Если реальная опора препятствует только одному перемещению, то на схеме ставят шарнирно-подвижную опору.

В случае опоры, препятствующей двум линейным перемещениям в плоскости рамы, на схеме изображают шарнирно-неподвижную опору.

В опорах возникают опорные реакции: в заделке – изгибающий момент и две силы (вертикальная и горизонтальная); в шарнирно-подвижной − одна сила; в шарнирно-неподвижной – две взаимно перпендикулярные силы. При этом число опорных реакций не должно быть менее трёх, иначе рама станет геометрически изменяемой, т. е. получит смещения и не будет уравновешенной системой. Так рама, изображённая на рис. 7.1, имеет шарнирно-подвижную и шарнирно-неподвижную опоры, и общее количество опорных реакций равно трём, рама геометрически неизменяемая.

Значения опорных реакций необходимы для расчёта рам. Для вычисления опорных реакций в случае плоской рамы составляют три уравнения равновесия, чаще используют следующие:

∑ F_z = 0; ∑ M_А = 0, ∑ M_В = 0, (7.1)

оставляя неиспользованное уравнение ∑ F_y = 0 для проверки реакций.

Как известно, для расчётов на прочность и жёсткость необходимо знать внутренние усилия, которые определяются известным методом сечений по правилу РОЗУ: р азрезать, о тбросить, з аменить, у равновесить.

Необходимо выполнять разрез на каждом грузовом участке рамы и рассматривать равновесие отсечённой части, составляя уравнения равновесия

∑ F_z = 0; ∑ F_y = 0, ∑ M_О = 0, (7.2)

Как следует из (7.2), равновесие соблюдается, если в сечении рамы возникают три вида внутренних усилий: продольная сила N, поперечная сила Q и изгибающий момент M, поэтому для плоских рам строят три эпюры: эпюры N, Q, M, − это весьма трудоёмкий пункт расчёта рам.

Чтобы успешно выполнить построение эпюр,нужно помнить принципы построения эпюр продольных сил N при растяжении-сжатии, эпюр поперечных сил Q и изгибающих моментов M при плоском изгибе балок.

Так как в сечениях плоских рам возникают одновременно продольные силы 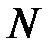и изгибающие моменты M=M_x, то наблюдается сложное сопротивление: совокупность осевого растяжения-сжатия и плоского изгиба. Тогда нормальные напряжения σ есть сумма напряжений от осевого растяжения-сжатия и плоского изгиба:

.

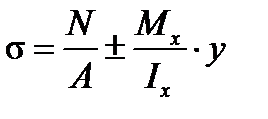Но слагаемое 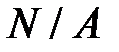часто составляет малую часть от всего нормального напряжения σ: стержни плоской рамы работают в основном на изгиб, в виду этого для плоских рам условие прочности записывают в виде:

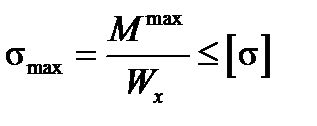. (7.3)

Условие (7.3) составляют для опасного сечения рамы, в котором на эпюре изгибающих моментов находится .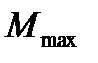

От поперечных сил Q возникаю касательные напряжения τ, которые вычисляют по формуле Д.И. Журавского. При расчёте рам, когда необходимо, используют условие прочности по касательным напряжениям, и также условие прочности по теориям прочности, учитывающим одновременное наличие нормальных и касательных напряжений.

Дата добавления: 2015-06-04