Построение эпюр внутренних усилий

Определение опорных реакций

Пример решение задачи 7

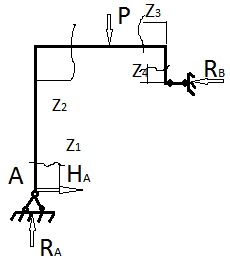
Для рамы (рис. 7.2, а) длина =1,2 м, сила Р =30 кН. Построить эпюры продольных сил, поперечных сил и изгибающих моментов.

Для вычисления опорных реакций составим уравнения равновесия по (7.1).

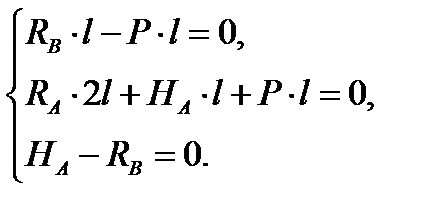
Получаем 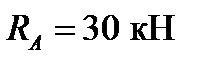, 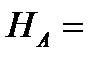30 КН, 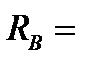30 кН.

Проверим реакции неиспользованным уравнением ∑ F_y = 0:

, , ,

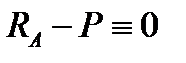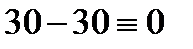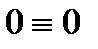значит, реакции найдены верно.

В плоской раме возникают три вида внутренних усилий: продольная сила 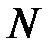,поперечная сила Q и изгибающий момент M. Построим их эпюры. Разделяем раму на грузовые участки. В рамах границами участков являются также и узлы. Поэтому имеем четыре силовых участка. Абсциссы z текущих сечений для всех участков показаны на рис. 7.2, б.

Правила знаков продольных сил N при растяжении-сжатии и эпюр поперечных сил Q и изгибающих моментов M такие, как при растяжении-сжатии и при плоском изгибе балок.

Рассматривая равновесие отсечённой части, наблюдатель находится внутри рамы лицом к стержню.

1-й участок: 0 ≤ z ₁ ≥ 2 l. Составляя уравнения (7.2) для отсечённой части 1-го участка (рис. 7.2, б), получаем

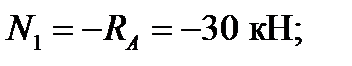
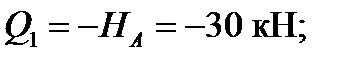
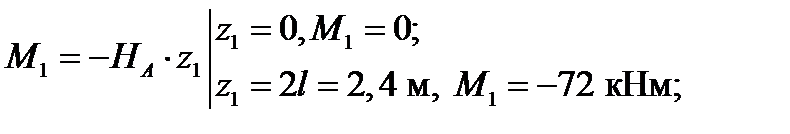
имеем сжатые волокна справа.

2-й участок: 0 ≤ z ₂ ≥ l:

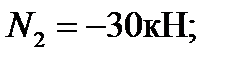
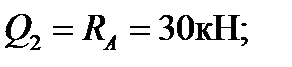
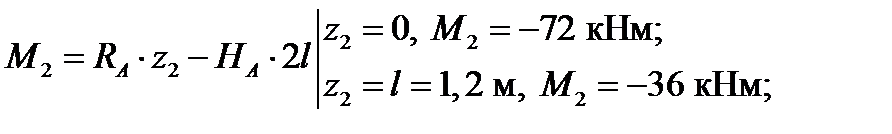
имеем сжатые волокна снизу.

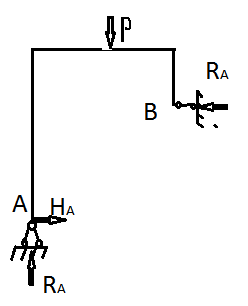I II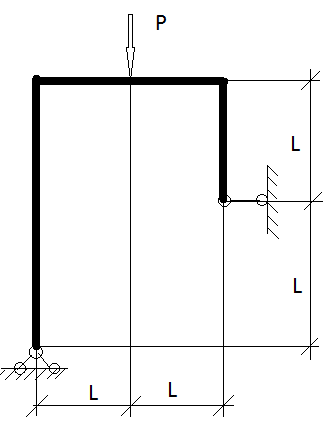
a	б	в
г	д	е

Рис. 7.2

3-й участок: 0 ≤ z ₃ ≥ l.

Координату z ₃ для удобства отсчитываем справа, при этом получаем:

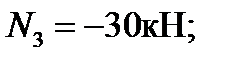
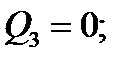
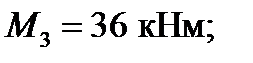
имеем сжатые волокна снизу.

4-й участок: 0 ≤ z ₄ ≥ l.

Начало координаты z ₄ выбираем на опоре В, для отсечённой части 4-го участка получаем

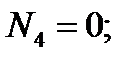
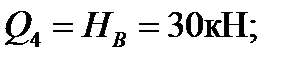
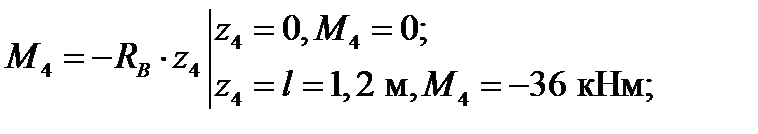
имеем сжатые волокна слева.

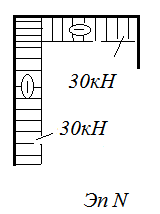
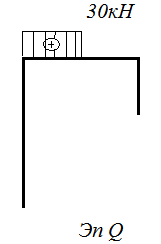
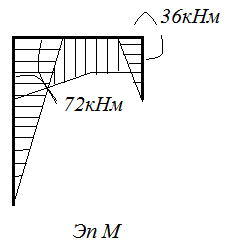
Откладывая полученные значения на схемах рамы, построим эпюры N, Q, M (рис. 7.2, в, г, д). При этом положительные значения сил откладываем снаружи рамы, отрицательные – внутри.

Эпюры изгибающих моментов строим, откладывая значения моментов со стороны сжатых волокон. В этом случае говорят, что строят эпюру моментов на сжатых волокнах. Необходимо заметить, что в расчётах строительных конструкций эпюры изгибающих моментов чаще строят на растянутых волокнах.

Правила контроля эпюр Q и М в рамах те же, что для балок. К правилам контроля для рам добавляется следующее: все узлы рамы должны находиться в равновесии под действием сил и изгибающих моментов.

Используем это правило. Двумя бесконечно близкими сечениями вырежем узел I (рис. 7.2, а), изобразим его отдельно (рис. 7.3, а) и приложим к нему соответствующие внутренние усилия, значения которых возьмём из эпюр N, Q, M (рис. 7.1, г, д, е).

Составляем уравнения равновесия по (7.2) для узла I:

∑ F_z = 0: 30 – 30 = 0;

∑ F_y = 0: 30 – 30 = 0;

∑ M (уз I) = 0: 72 – 72 = 0;

Убеждаемся, что узел I находится в равновесии.

Аналогично проверяется равновесие узла II (рис. 7.3, б).

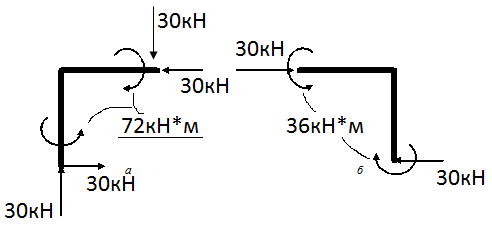
Узел I а	Узел II б

Рис. 7.2

Таблица 7.1. Схемы рамы к задаче 7

		6

Таблица 7.1. Схемы рамы к задаче 7 (продолжение)

19

Таблица 7.1. Схема рамы к задаче 7 (окончание)

Таблица 7.2. Исходные значения к задаче 7

	Длина , М	Сила Р, кН	Номер варианта	Длина , М	Сила Р, кН
	1,10			1,55
	1,80			1,70
	1,75			1,40
	1,80			2,00
	1,70			1,80
	1,60			2,10
	1,90			1,35
	1,65			2,20
	0,95			1,10
	1,85			1,75
	1,20			2,05
	2,00			1,85
	1,30			1,20
	1,50			1,25
	1,40			1,60

Задача 8

Дата добавления: 2015-06-04