
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Построение эпюр поперечных сил и изгибающих моментов
|
|
|
|
Вычисление опорных реакций
Пример решения задачи 5
Выполним расчёт при следующих значениях: сосредоточенные силы. Р 1 = 0 и Р 2 = 16кН, сосредоточенные моменты М 1 = 0 и М 2= -30 кН∙м, интенсивность распределённой нагрузки q 1 = 0 и q 2 = -20 кН/м, длины участков L 1 = 2 м и L 2 = 3 м.
Сначала по заданным значениям построим реальную балку (см. рис. 5.4, б). Далее для выполнения расчётов нужно знать величины реактивных сил RA и RB, возникающих в опорах А и В, которые вычислим из уравнений равновесия балки
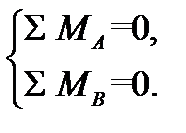
Для данной балки они принимают вид:
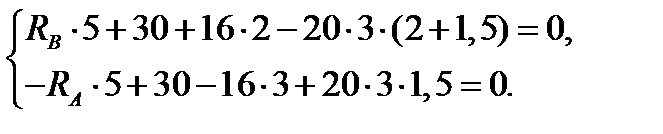
Из этих уравнений получаем 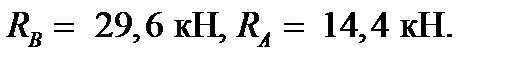
Для проверки правильности найденных реакций опор составим неиспользованное уравнение равновесия
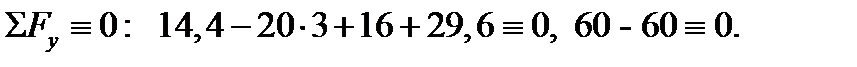 :
:
Имеем тождество, значит, реакции опор найдены верно.
В поперечных сечениях балки возникают поперечные силы Qy и изгибающие моменты Мх. Значения Qy и Мх изменяются вдоль балки, для получение их максимальных значенийстроят графики ̶ эпюры Qy и Мх. Значения Qy и Мх вычисляют по участкам балки. Границами участков являются сечения, в которых приложены сосредоточенные моменты и силы, а также начало и конец распределённой нагрузки. Для каждого участка применяются правила РОЗУ метода сечений:
1) Р азрезать балку на 2 части.
2) О тбросить одну из частей.
3) З аменить воздействие отброшенной части на оставленную усилиями Qy и Мх.
4) У равновесить внешнюю нагрузку и внутренние усилия Qy и Mx, составив два уравнения равновесия отсечённой части:
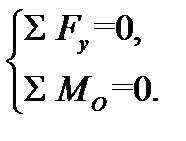 (5.2)
(5.2)
Заметим, что здесь за точку О выбираем центр тяжести текущего сечения, и составляем уравнение моментов относительно этой точки от всех воздействий, действующих на оставленную часть балки.
Разобьём балку на два грузовых участка(рис. 5.4, а) и рассмотрим вычисление усилий Qy и Mx на каждом.
1-й участок: 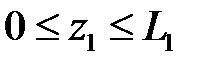 , где z 1– координата текущего сечения. Рассмотрим кусок первого участка балки длиной z 1, расположенный по левую сторону от сечения. В сечении возникают изгибающие моменты Мх 1 и поперечные силы Qy 1, которые предполагаем положительного направления: поперечная сила положительна, если её вектор стремится повернуть рассматриваемую часть по часовой стрелке; изгибающий момент Mx в сечении будем считать положительным, если балка изгибается выпуклой стороной вниз.
, где z 1– координата текущего сечения. Рассмотрим кусок первого участка балки длиной z 1, расположенный по левую сторону от сечения. В сечении возникают изгибающие моменты Мх 1 и поперечные силы Qy 1, которые предполагаем положительного направления: поперечная сила положительна, если её вектор стремится повернуть рассматриваемую часть по часовой стрелке; изгибающий момент Mx в сечении будем считать положительным, если балка изгибается выпуклой стороной вниз.
Слева от сечения расположена только сила RA, поэтому записываем:
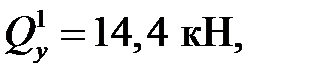 ,
, 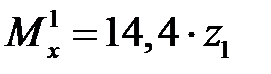 .
.
Выражение поперечной силы Qy 1 не содержит переменных, следовательно, на 1-м участке на эпюре Qy значение постоянно и равно 14,4 кН. Отложим вверх от нулевой линии это значение в масштабе и построим на 1-м участке эпюры Qy прямоугольник (рис. 5.4, в).
Выражение Мх 1 соответствует уравнению прямой. Подсчитаем величины моментов при граничных значениях (z 1=0 и z 1= l):
При z= 0 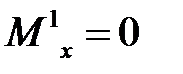 ; при
; при 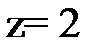 м
м 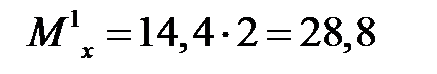 кН∙м.
кН∙м.
На базисной линии отложим эти значения и проводим наклонную прямую эпюры Mх на 1-м участке (рис. 5.4, г).
| а б в г |  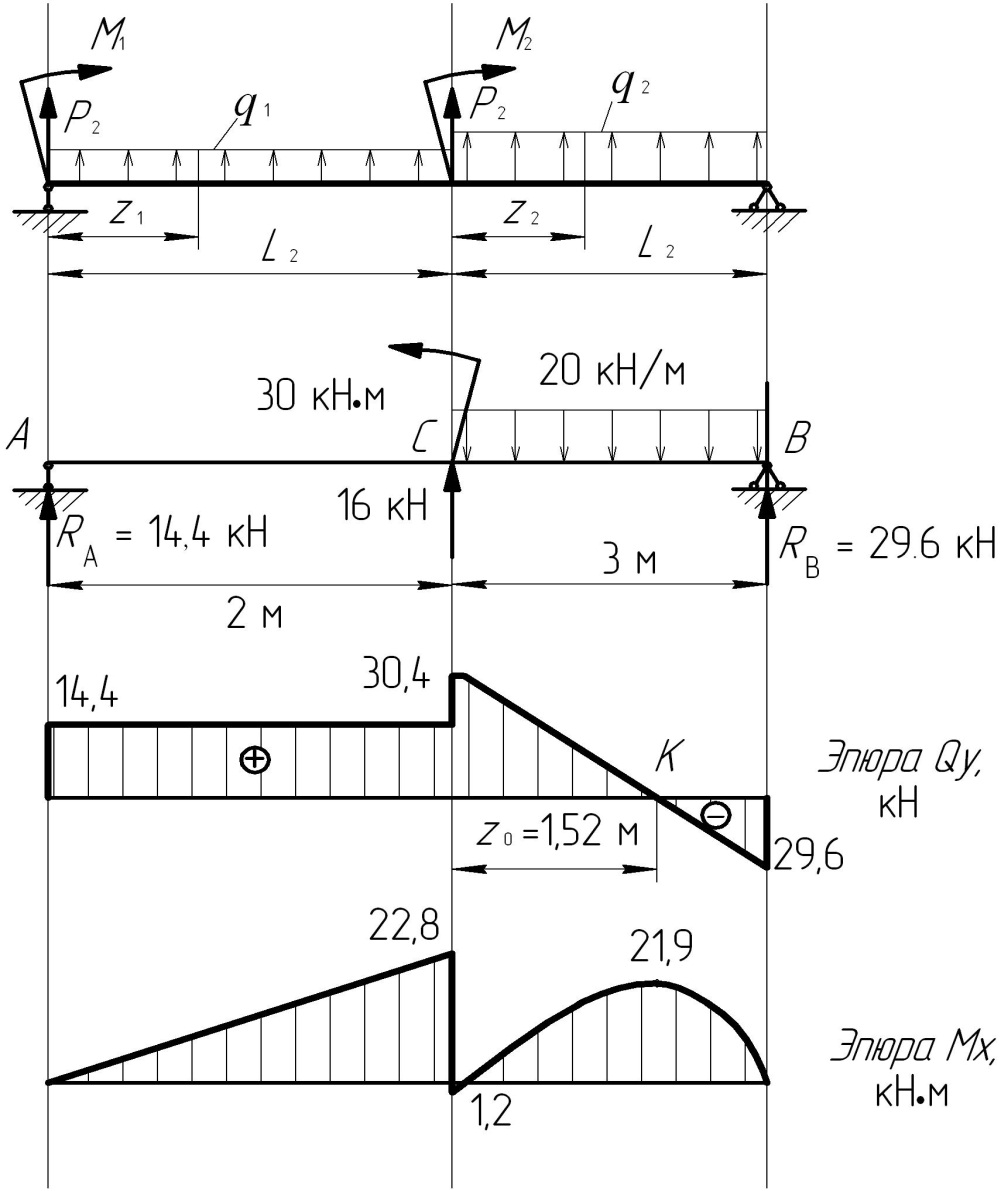
|
Рис. 5.4
Рассмотрим 2-й участок:  . Возьмём участок балки слева от сечения и по (5.2) получаем
. Возьмём участок балки слева от сечения и по (5.2) получаем
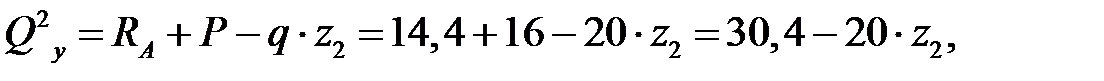
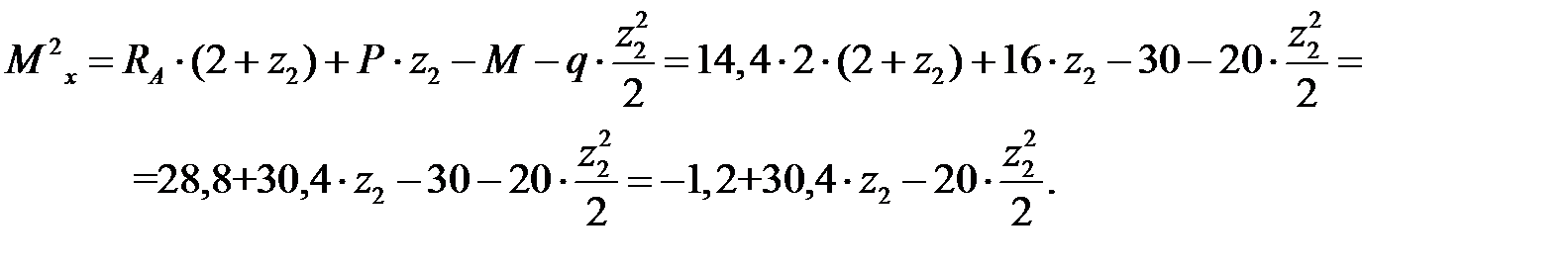
Подсчитаем значения 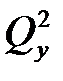 и
и 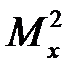 для граничных значений
для граничных значений 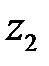 :
:
при z2= 0 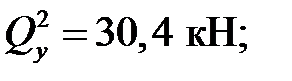
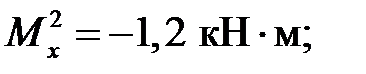
приz2= 3 м  кН;
кН; 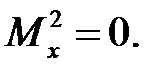 .
.
По найденным значениям поперечных сил и изгибающих моментов построим эпюры Qy и Mx на 2-м участке. Сила  изменяется линейно, поэтому, отложив в начале 2-го участка
изменяется линейно, поэтому, отложив в начале 2-го участка 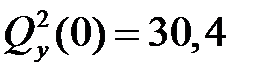 кН и в конце
кН и в конце 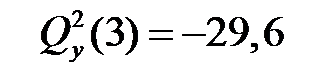 кН, соединим эти точки наклонной прямой (рис. 5.4, в), которая пересекает базисную линию в точке К. Так как функция момента
кН, соединим эти точки наклонной прямой (рис. 5.4, в), которая пересекает базисную линию в точке К. Так как функция момента  имеет второй порядок по отношению к переменной z 2(это результат наличия распределённой нагрузки на этом участке), то при изображении момента должны изобразить параболу.
имеет второй порядок по отношению к переменной z 2(это результат наличия распределённой нагрузки на этом участке), то при изображении момента должны изобразить параболу.
Уточним вид этой параболы с помощью эпюры Qy и теоремы Д.И. Журавского (4.3) об интегрально-дифференциальной зависимости функций Qy и Мx. На эпюре сил Qy имеем пересечение наклонной линии Qy с базисной прямой (в точке К). Это внесёт следующую поправку в изображение параболы: в точке К получается перегиб кривой, и момент  получает экстремальное значение
получает экстремальное значение  . Для вычисления момента
. Для вычисления момента  необходимо найти абсциссу этого сечения
необходимо найти абсциссу этого сечения  . Величину
. Величину  определяем из уравнения
определяем из уравнения 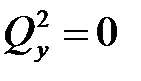 , которое принимает вид:
, которое принимает вид: 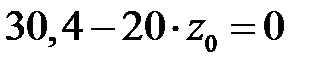 . Получаем
. Получаем 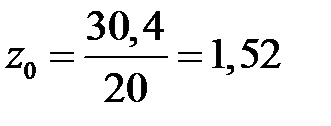 м.
м.
Подсчитаем значение экстремального момента 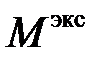 как момента
как момента  при
при 
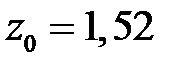 м:
м:
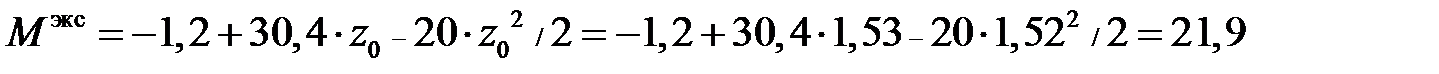 кН·м.
кН·м.
Отложив значения моментов в начале, в конце участка и в сечении К, построим эпюру моментов на 2-м участке (рис. 5.4, г). Целью построения эпюр является получение максимального (расчётного) значения M max. На построенной эпюре моментов M max=28,8кН·м.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 1668; Нарушение авторских прав?; Мы поможем в написании вашей работы!