Теоретические основы решения. Проверочный расчёт консольной балки

Условие задачи

Проверочный расчёт консольной балки

Для стальной двутавровой балки (см. рис. 4.2, а) известна внешняя нагрузка, размер сечения и длина балки даны в табл. 4.1.

Требуется:

1. Построить эпюры внутренних усилий: поперечной силы Q_y и изгибающего момента М_x.

2. Проверить прочность балки, используя условие прочности по нормальным напряжениям. Принять допускаемое напряжение [σ] = 200 МПа.

3. Принимая схему балки как схему мостовой балки подъёмного крана, найти наибольшее нормальное напряжение σ_max, возникающее при торможении, при котором за счёт сил инерции угол наклона нагрузки составил 10⁰ к вертикали.

Изгиб ¾ это часто встречаемый вид деформации прямолинейных элементов машин, механизмов и строительных конструкций, и поэтому плоский изгиб является важнейшим разделом сопротивления материалов, и ему уделяется большое внимание.

а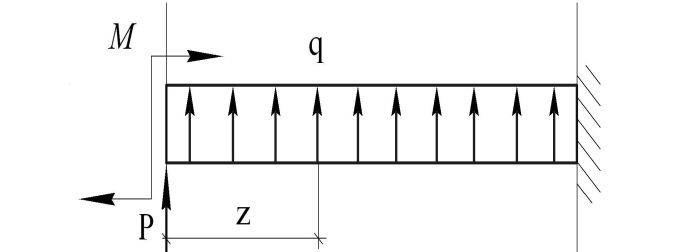
б

Рис. 4.1

При расчёте прямолинейные элементы изображают в виде прямого бруса (рис. 4.1). Рассмотримнагрузку (рис. 4.1, а) в вертикальной плоскости бруса, совпадающей с его главной плоскостью инерции. Пусть действуют сосредоточенная сила Р, момент М и распределённая нагрузка интенсивности q. Деформация бруса выглядит как искривление (изгибание) бруса в плоскости нагрузки (рис. 4.1, б). При этом наблюдается следующая картина деформирования продольных волокон: имеем растяжение продольных волокон с одной стороны от продольной оси бруса и сжатие с другой, а продольная ось лишь искривилась, и поэтому она называется нейтральной осью. Такой вид деформации носит название плоский изгиб, а брус, получающий изгиб, называют балкой. Итак, если воздействие нагрузки происходит в плоскости, перпендикулярной продольной оси бруса и проходящей через главную ось инерции сечения, то имеем плоский изгиб.

Рассмотрим расчёт балки для общего случая нагружения при плоском изгибе (рис. 4.2): при наличии распределённой нагрузки, сосредоточенной силы и сосредоточенного момента.Направление нагрузок считаем положительным, если нагрузка отгибает балку к верху и вызывает растяжение нижних волокон.

Для расчёта балки необходимо знать внутренние усилия, вычислениекоторых производится методом сечений по правилу РОЗУ(рис 4.2). Последовательно выполняются следующие действия:

1) р азрезать балку на две части;

2) о тбросить одну из частей;

3) з аменить воздействие отброшенной части на оставленную внутренними усилиями;

4) у равновесить внешнюю нагрузку и внутренние усилия.

Рассмотрим эту методику на примере консольной балки (рис 4.2, а). Так как схема нагружения не изменяется по всей длине консоли, то имеем один грузовой участок, и достаточно рассмотреть один разрез балки на две части. На схеме балки покажем положение разреза координатой z (рис. 4.2, а).

Далее нужно рассмотреть одну из частей: либо левую, либо правую. На рис 4.2, б изображены обе части. Из них для расчёта левой части нужны значения опорных реактивных усилий R _зад и М _зад, возникающих в заделке, так как реактивные воздействия - часть внешней нагрузки, а в расчёт правой эти усилия не войдут, поскольку они не действуют на неё. Поэтому проще рассматривать правую часть, т. е. внутренние усилия в консольных балках лучше вычислять со свободного края. Итак, рассмотрим отсечённую правую часть длиною z. Сечение с координатой z называют текущим сечением.

Имеем 0 ≤ z ≤ l. В текущем сечении отсечённой части покажем внутренние усилия: поперечную силу Q_y и изгибающий момент M_x, причём строго определённого направления.

а б в д

Рис. 4.2

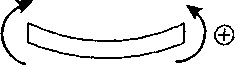
При изображении Q_y и M_x нужно пользоваться общепринятым правилом знаков:сила Q_y положительна, если вектор силы вращает оставленную часть по часовой стрелке; момент M_x положителен, если растягивает нижние волокна (рис. 4.3).

Сила Q_y > 0 Момент М_х > 0

Рис. 4.3

Остановимся насоставлении уравнений равновесия. Оставленная часть балки нагружена в одной и той же плоскости внешней нагрузкой и внутренними усилиями Q_y и M_x. Имеем плоскую систему сил, для которой существуют три уравнения равновесия; в плоской системе координат (у, z) они имеют вид:

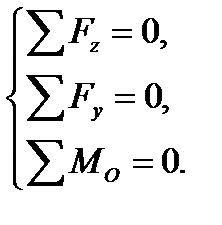
Заметим, что за точку О здесь удобнее взять центр тяжести текущего сечения.

При плоском изгибе отсутствуют продольные воздействия вдоль оси балки (вдоль оси z), и первое уравнение превращается в тождество 0=0, поэтому при расчёте балок оставляют лишь два уравнения:

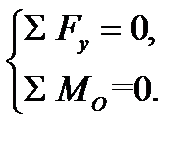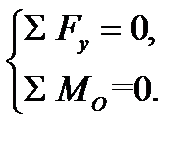. (4.1)

Запишем уравнения (4.1) для отсечённой левой части рассматриваемой консоли:

, ,

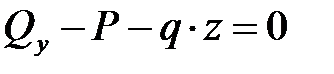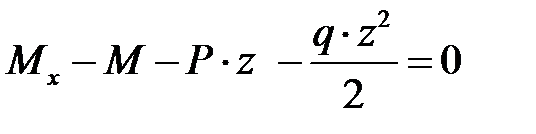из которых получаем выражения:

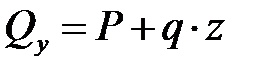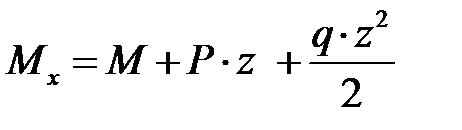, . (4.2)

Выражения (4.2) представляют по сути формулы для сил Q_y и моментов М_x, в них входят все виды нагрузок, и при подстановке в эти формулы значений реальных нагрузок получаем значения Q_y и М_x для реальной балки. По (4.2) видно, что в общем случае для силы Q_y имеем линейную зависимость, а для моментов М_x - криволинейную. Заметим, что между Q_y и M_x существует соотношение, которое известно как теорема Д.И. Журавского: если взять производные от функции M_x по z и от функции Q_y по z, то получим

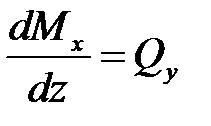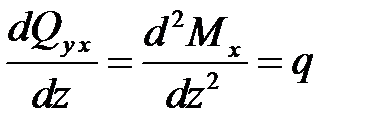, . (4.3)

Вычислим значения Q_y и М_x в начале балки (при z = 0) и в конце (при z = l). Получим граничные значения Q_y и М_x:

при z =0 Q_y = , ;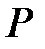

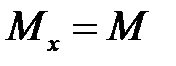при z = l Q_y = , .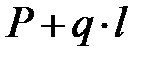

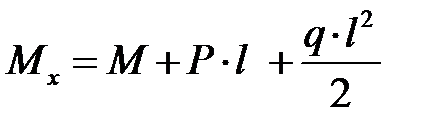Значения сил Q_y и моментов М_x изменяются вдоль балки, для выбора максимальных значений Q_y и M_x (т.е. расчётных значений) изображают графики их изменения вдоль балки, которые называются эпюрами поперечных сил Q_y и изгибающих моментов M_x (рис 4.2). Построение эпюр проводят, используя найденные значения Q_y и М_x. Для этого отложим эти значения от базисной линии (эта линия, проведённая под балкой параллельно оси балки). Далее проводим наклонную прямую для Q_y и параболу для М_x.

На рис. 4.4 приведены эпюры поперечных сил Q_y и изгибающих моментов M_x в консольной балке отдельно от сосредоточенной силы, сосредоточенного момента и от распределённой нагрузки, которые хорошо показывают зависимость линий эпюр от вида нагрузки.

При расчётах элементов машин и механизмов положительные моменты откладываются вверх от базисной линии, с этой стороны расположены сжатые волокна, поэтому говорят, что эпюру изгибающих моментов строят со стороны сжатых волокон. Для строительных конструкций построение эпюр обычно выполняют на растянутых волокнах. Этот факт связан с использованием графоаналитических методов расчёта, т. е. исторически закрепилось построение на растянутых волокнах. Знак момента на эпюре обычно не ставится, так как для описания прочности используется модуль момента, а не его направление.

От изгибающих моментов M_x в сечении балки возникают нормальные напряжения σ, от поперечных сил Q_y ─ касательные напряжения τ. Решающее влияние на прочность балок имеют нормальные напряжения, поэтому составляют условие прочности по нормальным напряжениям:

, (4.4)

где σ_max ¾ максимальное напряжение в опасном сечении балки, в котором модуль изгибающего момента M_x принимает максимальное значение M _max, значение момента M _max называют расчётным; 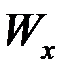¾ осевой момент сопротивления сечения, 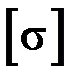¾ допускаемое напряжение для материала балки.

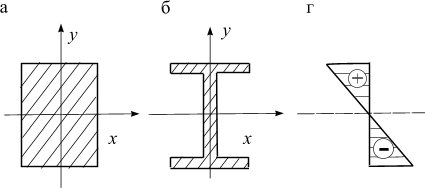
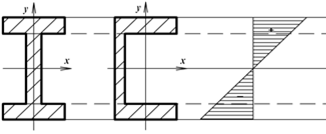
Согласно с видом деформирования при изгибе балки (рис. 4.1) со стороны растянутых волокон возникают растягивающие напряжения, со стороны сжатых волокон ¾ сжимающие, и те и другие принимают наибольшее значение в крайних верхних и нижних точках сечения. Поэтому, если материал балки одинаково хорошо сопротивляется растяжению и сжатию, используют сечения, симметричные по высоте: прямоугольник, двутавр, швеллеры, круг и др. (рис. 4.5). Для симметричных сечений эпюра напряжений σ по высоте сечения линейна и симметрична.

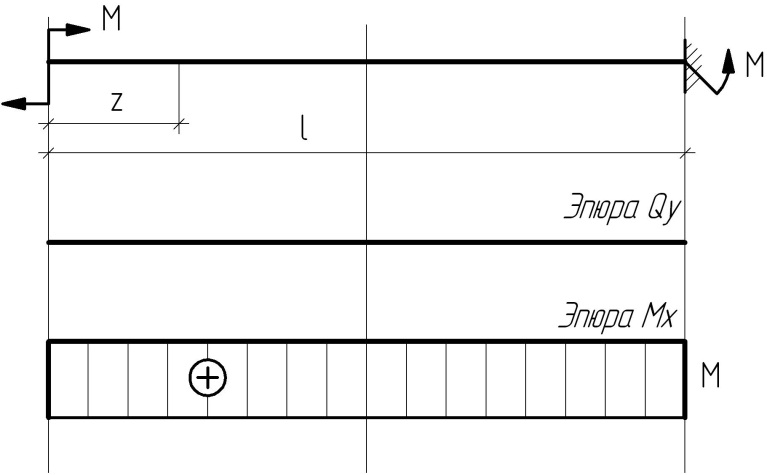
Балка 1	В текущем сечении z Qy= 0, Mx = M= const
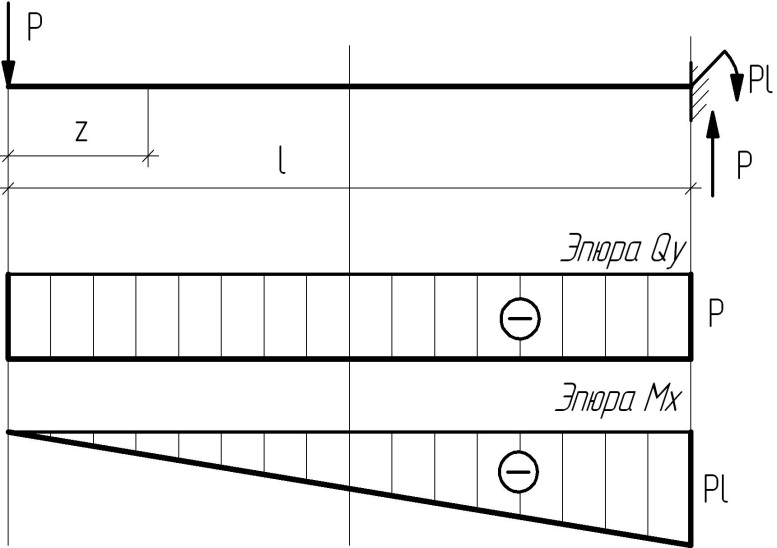
Балка 2	В текущем сечении z Qy= - P= const, Mx = - P·z. При z= 0 Mx =0, при z=l Mx =- P·l.
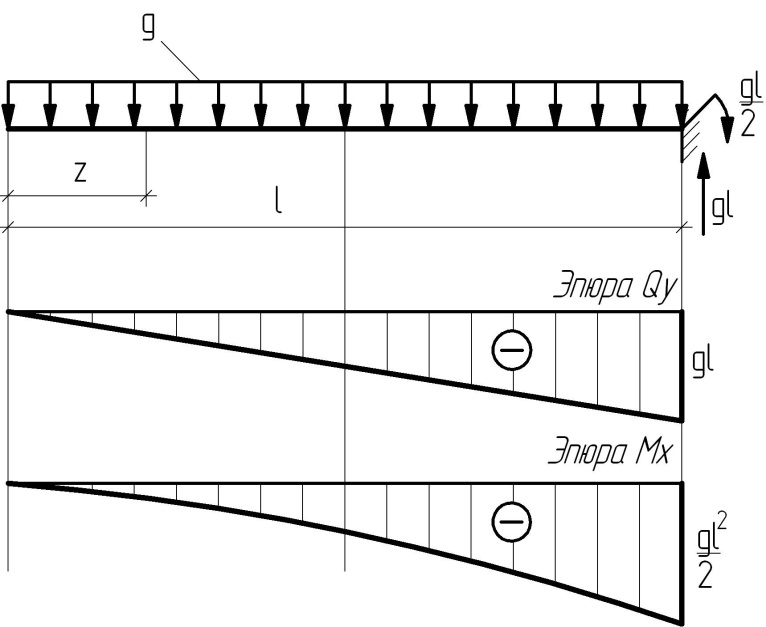
Балка3	В текущем сечении z Qy= - q·z, Mx= - q·z ^2 / 2. При z= 0 Qy= 0, Mx =0; при z=l Qy= - q·l, Mx =- q·l ^2 / 2.

Рис. 4.4

Эпюра σ  

Рис. 4.5

По условию прочности (4.4) можно выполнять следующие три вида расчётов:

проектный, когда определяют требуемые размеры поперечного сечения балки;

проверочный, при котором вычисляют напряжения и сравнивают с допускаемыми;

определение нагрузочной способности, когда находят допускаемые значения внешней нагрузки.

Дата добавления: 2015-06-04