Пример решения задачи 4

Выполним расчёт балки при следующих значениях: сечение стальной балки ‒ двутавр № 20; l = 4 м; q = - 8 кН/м; P = 12 кН; М = 12 кН∙м;

1. Построение эпюр поперечной силы и изгибающего момента.

Сначала изобразим балку, поставив нагрузку согласно их значениям (рис. 4.6, а). Значения поперечной силы Q_y и изгибающего момента М_x вычислим по функциям (4.2), подставляя заданные значения. Получаем линейную функцию поперечной силы Q_y и криволинейную для изгибающего момента М_x:

, .

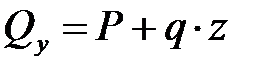
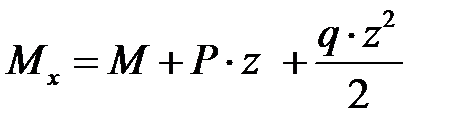
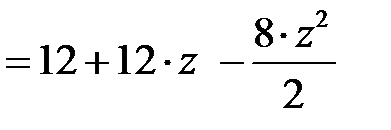Подсчитаем значения в начале балки (при z = 0) и в конце (при z = l) (граничные значения силы и момента):

при z = 0 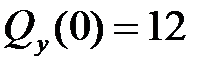кН; кН∙м;

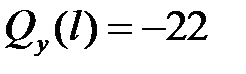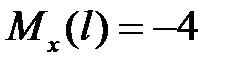при z = l = 0,2 м кН; кН∙м;

Построим эпюры поперечной силы Q_y и изгибающего момента М_x (рис. 4.6, б, в). Сначала под чертежом балки проводим две базисные линии, параллельные оси балки. Далее в характерных точках первой базисной линии откладываем значения силы Q_y: в начале балки (z = 0) положительное 12 кН вверх от линии, в конце балки (при z = l = 0,2 м) отрицательное (-22 кН) ̶ вниз. Эти точки соединяем наклонной прямой. Получили график силы Q_y,

а б в

Эпюра Qy, кН     Эпюра Мх, кНм

Рис. 4.6

который называется эпюрой Q_y, её штрихуют перпендикулярно к базисной линии и ставят знак силы (+ и -).

На второй базисной линии откладываем значения М_x: для начального сечения балки положительное 12 кН∙м вверх, для конечного отрицательное (- 4 кН∙м) вниз. Соединять полученные точки нужно кривой второго порядка (по виду функции М_x параболой). Уточнить вид параболы можно с помощью эпюры Q_y и теоремы Д.И. Журавского (4.3), которая демонстрирует интегрально-дифференциальную зависимость функций Q_y и М_x. Так, когда наклонная прямая на эпюре Q_y пересекает базисную линию (как имеем в сечении К на построенной эпюре Q_y), то в этом сечении Q_y = 0, и поэтому угол наклона касательной к кривой М_x равен 0, т.е. касательная параллельна базисной линии. Здесь на кривой М_x наблюдается перегиб, и функция М_x имеет экстремум (это есть значение изгибающего момента в сечении К). Значение нужно найти.

Сначала, используя значение ,составим уравнение поперечной силы, из которого определим величину координаты z _К сечения К:

12-8 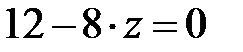z _К = 0. Получаем z _К м.

Подставив z _К =1,5 м в функцию М_x, подсчитаем значение экстремального момента: кН∙м.

Отложим это значение в сечении z _К и соединим полученные три точки моментов параболой. Получили график силы М_x, который называется эпюрой М_x, её штрихуют также перпендикулярно базисной линии, но знак момента не ставят.

Согласно полученной эпюре моментов опасным сечением является сечение К, и максимальное значение момента M _max= .

Дата добавления: 2015-06-04