Теоретические основы решения. Для стальной двухопорной балки, схема которой приведена на рис

Условие задачи

ПРОЕКТНЫЙ РАСЧЁТ ДВУХОПОРНОЙ БАЛКИ

Для стальной двухопорной балки, схема которой приведена на рис. 5.1, известна внешняя нагрузка и длины отрезков L ₁и L ₂. Числовые значения заданы в табл. 5.1.

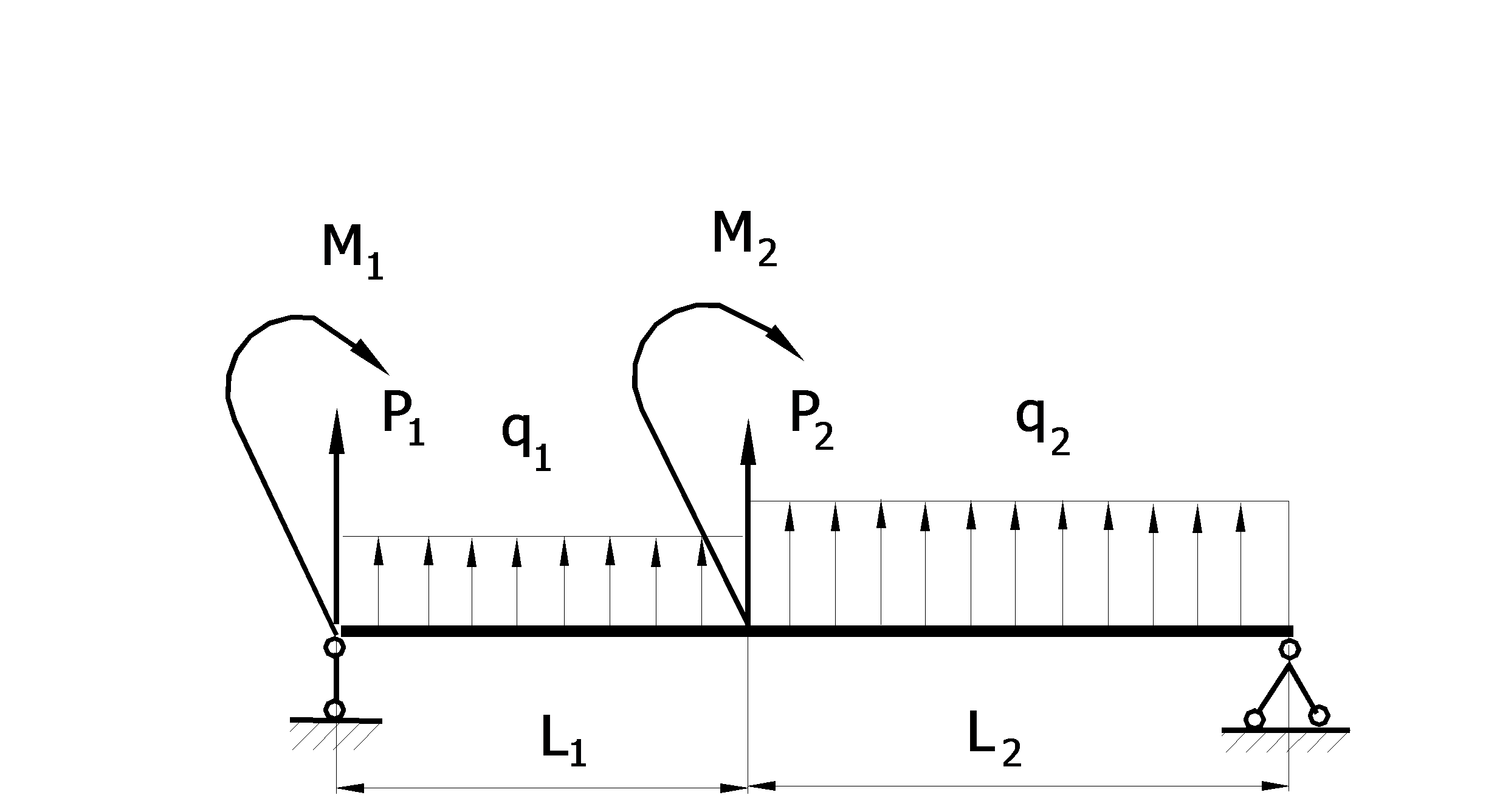
Рис. 5.1

Требуется:

1. Из уравнений равновесия балки вычислить силы реакций опор.

2. Составить выражения для поперечных сил Q_y и изгибающих момен­тов M_x по участкам балки, вычислить их значения в характерных сечениях и построить эпюры Q_y и M_x. Указать опасное сечение и значение M _max.

3. Из условия прочности по допускаемым напряжениям подобрать двутаврое, коробчатое и кольцевое сечения (рис. 5.2). Принятьдопускаемое напряжение [s]=200МПа. Сравнить расход материала по соотношению площадей и указать наиболее экономичное.

Рис. 5.2

В расчётах встречаются как консольные балки (балки с заделкой или защемлением), так и двухопорные балки. Если построение эпюр Q_y и M_x для консолей проще выполнять, начиная со свободного края, так как не нужно вычислять реакции в заделке, то для двухопорных балок сначала необходимо вычислить опорные реакции, а далее методика нахождения Q_y и M_x та же, что в задаче 4.

При построении эпюр Q_y и M_x, используют метод сечений. На рис. 5.3 изображены эпюры поперечных сил Q_y и изгибающих моментов M_x для трёх двухопорных балок, нагруженных отдельно сосредоточенной силой, моментом и распределённой нагрузкой. Они хорошо показывают зависимость линий эпюр от вида нагрузки.

В итоге укажем основные особенности эпюр Q_y и M_x. Они, с одной стороны, отражают теоретические закономерности и помогают при построении эпюр в любой балке, с другой стороны, знание особенностей позволяет контролировать правильность эпюр.

1. Если q = 0, поперечная сила Q_y всегда постоянна, и эпюра Q_y имеет вид прямоугольника, а изгибающий момент изменяется по линейному закону и на эпюре M _x− наклонная прямая.

В частном случае, когда при q = 0 и Q_y= 0, а изгибающий момент постоянен, на эпюре M_x имеется прямоугольник. Это случай чистого изгиба.

2. Если q ≠ 0, поперечная сила Q_y изменяется по линейному закону, и на эпюре Q_y будет наклонная прямая; изгибающий момент M_x имеет квадратичную зависимость от z, и на эпюре M_x будет кривая второго порядка (парабола), характер параболы определять с помощью эпюры Q_y. По теореме Д.И. Журавского тангенс угла α наклона касательной параболы (α ̶ это угол между касательной параболы и горизонтальной линией) равен Q_y, т. е.

значит, выпуклость или вогнутость параболы можно определить по значениям Q_y.

Если и на эпюре Q _yнаклонная прямая пресекла базисную линию, то в этом сечении угол α наклона касательной к кривой M_x равен нулю, касательная параллельна базисной линии, и момент в данном сечении экстремален для рассматриваемого участка.

3. В сечении, где приложена сосредоточенная сила P на эпюре поперечной силы Q_y будет скачок по направлению этой силы и на её величину, а на эпюре моментов M_x –перелом, направленный навстречу силе.

4. В сечении, где приложен сосредоточенный момент М,на эпюре поперечной силы Q_y нет изменений, а на эпюре моментов будет скачок на его величину по направлению М.

Целью построения эпюр является получение максимального модуля момента M_x ^max. Сечение балки, в котором изгибающий момент M_x принимает максимальное значение по модулю M_x ^max, называется опасным, а значение

Балка 1	В текущем сечении z 1 Qy= -M/l= const, Mx = - M/l · z 1. Mx (0) = 0; Mx (l/ 2) = -M/ 2. В текущем сечении z 2 Qy= -P/ 2 = const, Mx = P/ 2· z 2. Mx (0) = 0; Mx (l/ 2) = M/ 2;
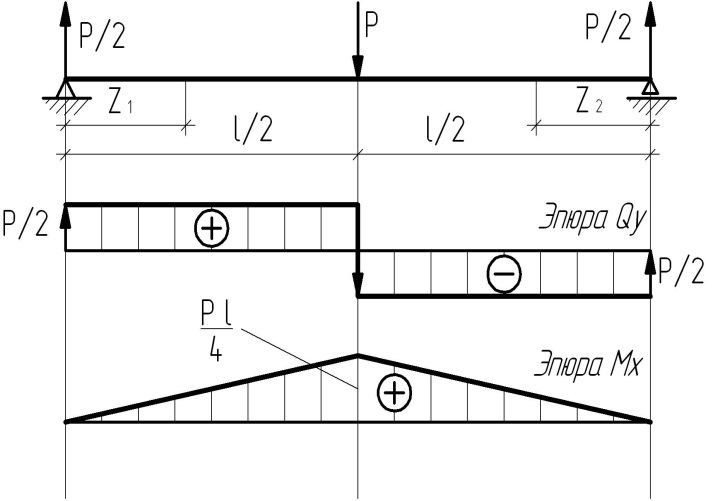
Балка 2	В текущем сечении z 1 Qy= P/ 2 = const, Mx= P/ 2· z. Mx (0)=0; Mx(l/ 2 ) = P·l/ 4.   В текущем сечении z 2 Qy= - P/ 2 = const, Mx= P/ 2· z. Mx (0) = 0; Mx(l/ 2)= P·l/ 4.
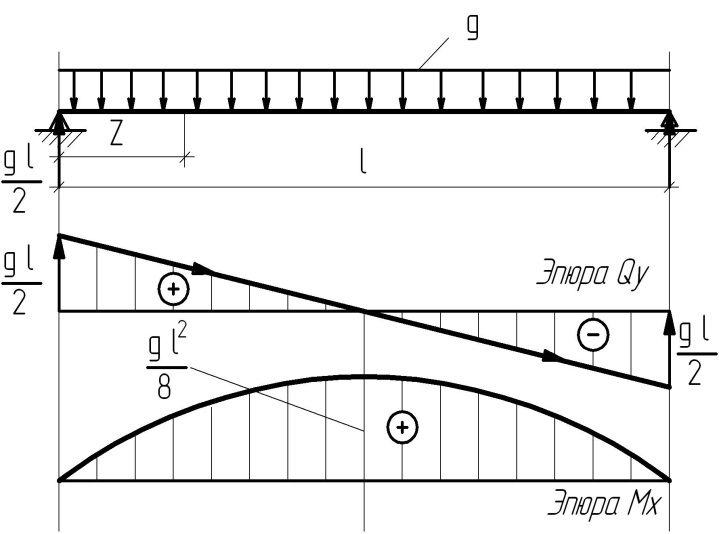
Балка 3	В текущем сечении z Qy= q·l/ 2- q·z, Mx= q·l/ 2· z - q·z ^2 / 2. Qy (0) = q·l/ 2, Mx (0) = 0; Qy (l/2) = 0, Mx (l/2) = q·l ^2 / 8. Qy (l) = - q·l/ 2, Mx (l) =0.

Рис. 5.3

момента M_x ^max = M _max─ расчётным. Для опасного сечения составляют условие прочности, которое описывает прочность балок.

Если балка выполнена из материала, который одинаково сопротивляется растяжению и сжатию, то для сечений балки используются симметричные по высоте фигуры: прямоугольник, двутавр, швеллеры и др.(рис. 4.5), и условие прочности в этом случае имеет вид:

, (5.4)

где [s] ¾ допускаемое напряжение для материала балки, W_x¾ момент сопротивления сечения относительно оси х, который вычисляется по формуле 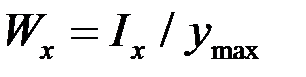через момент инерции сечения относительно горизонтальной оси х и расстояние по высоте .

Дата добавления: 2015-06-04