
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение допускаемой высоты падения
|
|
|
|
Статическое перемещение в месте удара
Используя указанное единичное состояние, запишем величину статического перемещения в месте удара  в виде произведения
в виде произведения
 =
=  ,
,
где 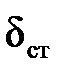 – единичное перемещение, это прогиб сечения С в единичном состоянии, которое найдём методом Мора. Тогда
– единичное перемещение, это прогиб сечения С в единичном состоянии, которое найдём методом Мора. Тогда

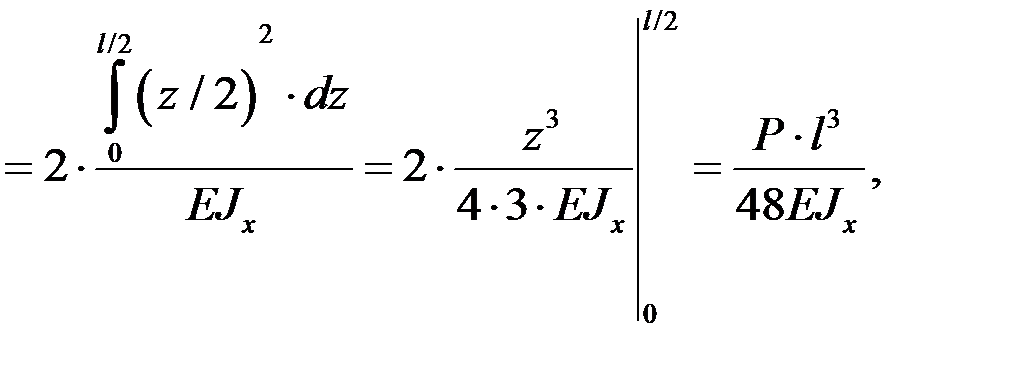
где 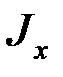 ¾ осевой момент инерции сечения, который выпишем из таблицы ГОСТ (табл. П.4 Приложения к данному пособию): для двутавра № 24
¾ осевой момент инерции сечения, который выпишем из таблицы ГОСТ (табл. П.4 Приложения к данному пособию): для двутавра № 24 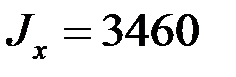 см4; Е ¾ модуль упругости материала балки, для стали Е = 2∙105 Мпа. Вычислим
см4; Е ¾ модуль упругости материала балки, для стали Е = 2∙105 Мпа. Вычислим 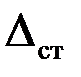 :
:
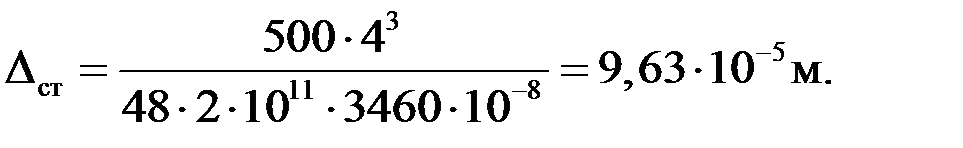
Определим допускаемую высоту  для случая абсолютно жёстких опор балки. Подставим найденные величины
для случая абсолютно жёстких опор балки. Подставим найденные величины 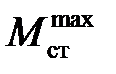 ,
,  и значение
и значение  см3 для двутавра № 24 (см. табл. П.4 Приложения) в условие прочности балки (9.3):
см3 для двутавра № 24 (см. табл. П.4 Приложения) в условие прочности балки (9.3):
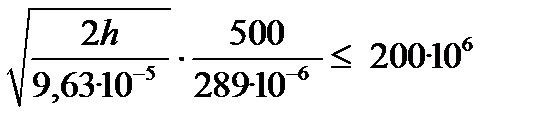 . (9.5)
. (9.5)
Отсюда высота падения  =
=  .
.
Принимаем допускаемую высоту падения при абсолютно жёстких опорах балки [ h ] = 0,64 м.
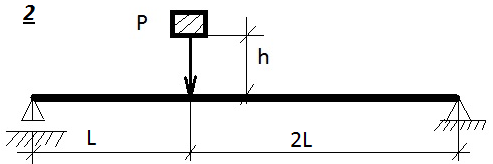
Определим допускаемую высоту падения  для случая, когда одна из опор упруго-податливая. Пусть опора В заменена на упруго-податливую, которую на схеме балки условно покажем пружиной (рис. 9.2, б). Она получает сжатие по направлению опорной реакции, это перемещение опоры называют осадкой. Для податливых опор имеется специальная характеристика – податливость λ, под которой понимается деформация опоры (осадка) от силы равной 1.
для случая, когда одна из опор упруго-податливая. Пусть опора В заменена на упруго-податливую, которую на схеме балки условно покажем пружиной (рис. 9.2, б). Она получает сжатие по направлению опорной реакции, это перемещение опоры называют осадкой. Для податливых опор имеется специальная характеристика – податливость λ, под которой понимается деформация опоры (осадка) от силы равной 1.
При действии статической силы P упругоподатливая опора получит осадку Δпр, пропорциональную величине реакции RВ:
Δпр = RВ ·λ = 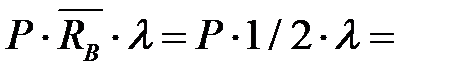 500·0,5·2,5·10-5 = 6,25 · 10-3м.
500·0,5·2,5·10-5 = 6,25 · 10-3м.
Если не учитывать изгибание балки, то за счёт осадки опоры В балка займёт наклонное положение (рис. 9.2, г). Сечение С переместится на величину СС 1 = Δ0. Пользуясь пропорцией (или подобием треугольников по схеме нового положения балки), запишем
Δ0 / Δпр = 0,5 l / l; тогда Δ0 = 0,5 ∙ Δпр = 0,5 ∙ 6,25 · 10-3 = 3,125 · 10-3м.
Прибавив к этой величине прогиб Δст от изгибания балки, получим полное новое значение перемещения сечения С:
Δст н =Δ0 + Δст = 3,125 · 10-3+3,125 · 10-5 = 3,125 · 10-3+0,03125 · 10-3  3,17 · 10-3м.
3,17 · 10-3м.
Подставим это значение вместо Δст в условие прочности (9.5):
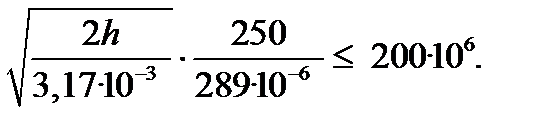
Из него получим новое значение высоты падения груза:
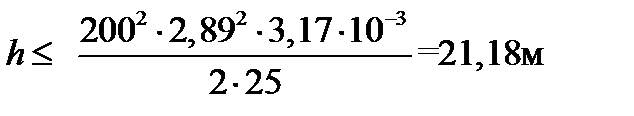 .
.
Теперь принимаем допускаемую высоту падения [ h ]=21м. Высота падения груза существенно увеличилась.
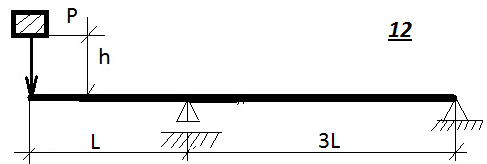
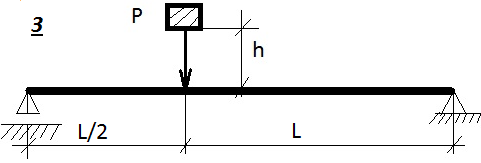
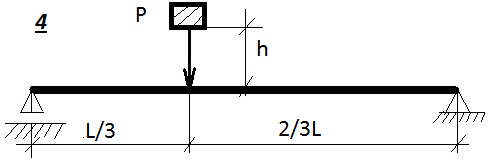
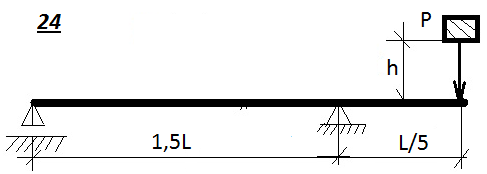
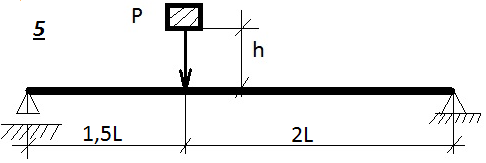
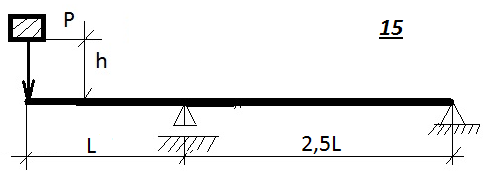
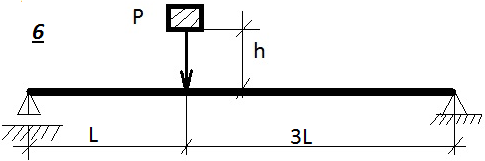
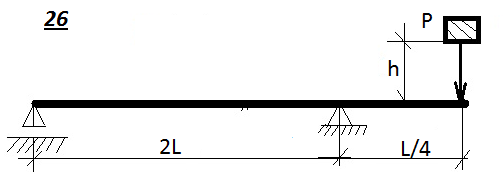
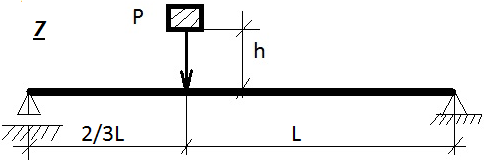
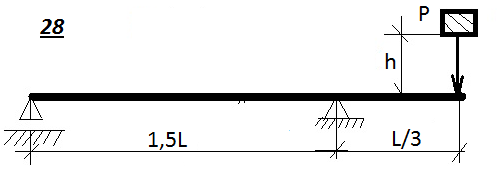
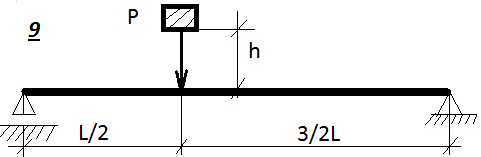
Таблица 9.1. Схемы к задаче 9

|
 
|
 
|
|
|  6 6

|
|  8 8

|
 
|
|
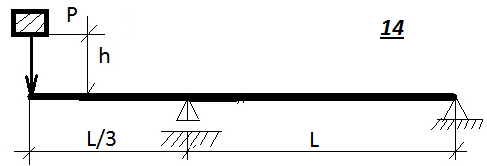
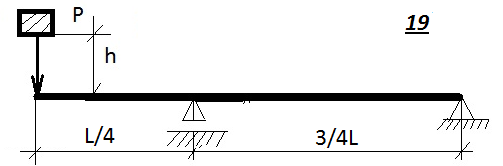
Таблица 9.1. Схемы к задаче 9(продолжение)
|
|
|
|
 
|
|
 
|
|
 19 19
|
 
|
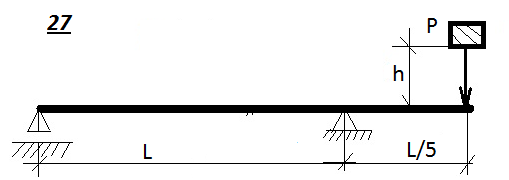
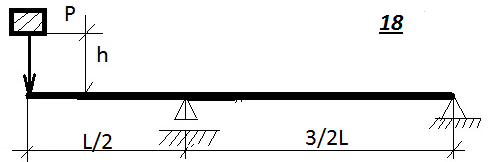
Таблица 9.1. Схемы к задаче 9 (окончание)
|
 
|
|
|
 25 25
|
|
 
|
 
|
 29 29

|  30 30

|
Таблица 9.2. Исходные данные к задаче 9
| Номер варианта | Длина 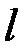 , м , м
| Вес сосредоточенного груза P, Н | Номер двутаврого сечения, № | Податливость λ∙105, м/Н |
| 3,8 | № 16 | 1,15 | ||
| 4,1 | № 18 | 1,25 | ||
| 4,2 | № 20 | 1,97 | ||
| 3,3 | № 24 | 1,65 | ||
| 3,4 | № 14 | 1,75 | ||
| 3,5 | № 27 | 2,05 | ||
| 2,9 | № 30 | 2,00 | ||
| 3,8 | № 40 | 2,50 | ||
| 3,7 | № 20 | 1,95 | ||
| 4,0 | № 24 | 1,85 | ||
| 5,1 | № 14 | 2,18 | ||
| 3,2 | № 16 | 2,40 | ||
| 4,3 | № 27 | 2,16 | ||
| 4,4 | № 18 | 2,94 | ||
| 4,5 | № 20 | 1,88 | ||
| 3,9 | № 24 | 1,72 | ||
| 4,1 | № 14 | 2,68 | ||
| 3,2 | № 16 | 2,73 | ||
| 3,3 | № 27 | 1,84 | ||
| 3,4 | № 30 | 1,78 | ||
| 3,5 | № 40 | 2,07 | ||
| 3,9 | № 27 | 3,17 | ||
| 3,8 | № 30 | 2,96 | ||
| 3,7 | № 20 | 2,33 | ||
| 4,0 | № 27 | 2,25 | ||
| 3,1 | № 16 | 1,82 | ||
| 3,2 | № 40 | 2,79 | ||
| 4,3 | № 27 | 2,26 | ||
| 3,4 | № 30 | 3,30 |
Задача 10
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 661; Нарушение авторских прав?; Мы поможем в написании вашей работы!