Пример решения задачи 10

Для центрально-сжатого стержня (рис. 10.2) длина стержня l = 4 м. Материал стержня ‒ сталь Ст. 5, вид поперечного сечения стержня задан схемой (рис. 10.2, б). Дано значение а = 30 мм = 3 см.

1. Определение допускаемой силы.

Условием устойчивости по коэффициенту φ (10.5) содержит допускаемое напряжение на устойчивость .

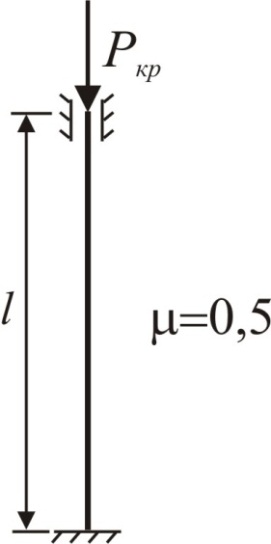
а	б

Рис. 10.2

Тогда значение допускаемой силы [ P _у] для центрально сжатого стержня равно

. (10.6)

Для вычисления [ P _у] нужно знать площадь А поперечного сечения заданного стержня и значение коэффициента , которое выбирается из табл.10.6 по значению гибкости данного стержня 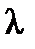, вычисляемой по формуле (10.2). Подставляем в эту формулу m (он указан на схеме стержня); 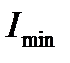– минимальный момент инерции заданного сечения ‒ это один из двух главных моментов инерции сечения I _max и I _min.

Главныемоменты инерции ̶ это моменты инерции относительно так называемых главных осей, в которых центробежный момент инерции равен нулю. Для выполнения расчётов нужно найти значения I _max, I _min и взять I _min.

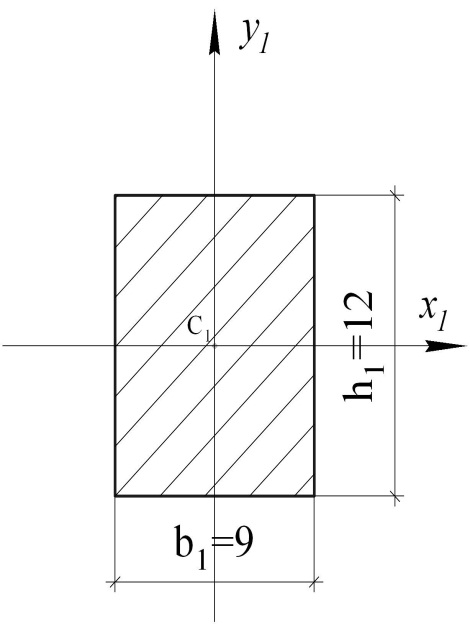
Сначала, используя заданное значение a = 3 см, выполним чертёж сечения в масштабе и проставим числовые значения характерных размеров (рис. 10.3, б).

Рассматриваемое сечение имеет следующие особенности.

Во-первых, сечение имеет две оси симметрии, поэтому центр тяжести всего сечения находится на их пересечении − в точке С ₁. Через эту точку проведём центральные оси всего сечения x_с и y_с (рис. 10.3, б).

Во-вторых, для рассматриваемого симметричного сечения центробежный момент инерции в осях x_с и y_с равен нулю, и это означает, что центральные оси всего сечения x_с и y_с есть главные оси, и центральные моменты инерции сечения и 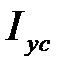есть искомые главные моменты инерции I _max, I _min.

В-третьих, рассматриваемое сечение ‒ составное, и моменты инерции нужно вычислять, используя моменты инерции отдельных фигур, составляющих сечение. Сечение можно представить состоящим из следующих простых фигур: прямоугольника высотой 4 а =12мм и шириной 3 а = 9ммидвух вырезов в виде полукругов диаметром 2 а= 6мм,т. е. составное сечение разложим на отдельные элементы (или фигуры). Присвоим им индексы i = 1, 2,3.

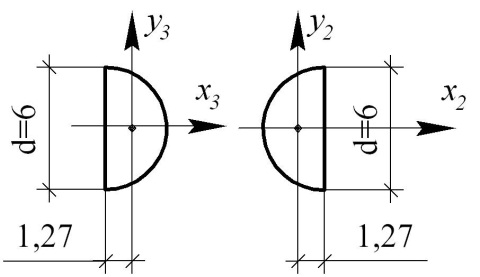
Изобразим эти элементы отдельно, нанесём их центры тяжести и через точки проведём собственные оси каждого элемента (см. рис. 10.3, в, г). Заметим, что центр тяжести полукруга удалён от диаметра (см. табл. П.5 Приложения к данному пособию) на расстояние, равное

.

а ─ Заданная схема сечения	б ─ Чертёж сечения
в ─ 1-й элемент сечения	г ─ 2-й и 3-й элементы сечения

Рис. 10.3

Оси элементов перенесём на составное сечение (рис. 10.3, б).

Возьмём за вспомогательные оси координат оси (x ₁, y ₁). Тогда координаты центра тяжести всего сечения равны нулю: x_с =0, y_с =0, и координаты центра тяжести каждой фигуры следующие:

, , .

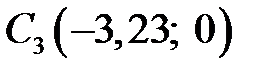Вычислим центральные моменты инерции всего сечения, используя формулы моментов инерции относительно параллельных осей:

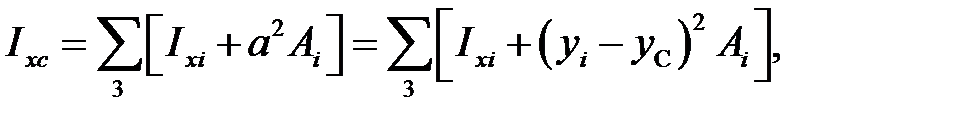
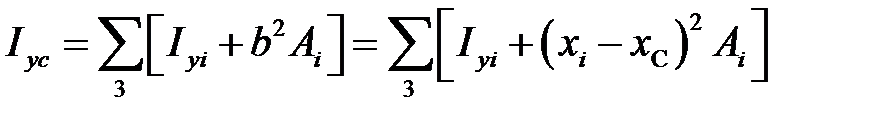, (10.7)

в которые входят геометрические характеристики элементов cечения: площади А_i, осевые I_xi, I_yi моменты инерции относительно собственных осей элементов (x_i, y_i); и расстояния между осями a_i = y_i - y _c, b_i = x_i - x _c.

Значения площади и моментов инерции элементов cечения относительно собственных осей элементов подсчитаем по формулам, представленным в таблице П.5 (см. Приложение к данному пособию).

Необходимо сделать следующее примечание: для отверстий площадь и моменты инерции считаем отрицательными. В нашем примере отверстиями являются полукруги, для них площадь и моменты инерции принимаем со знаком «‒».

Для 1 -го элемента (прямоугольника) получим

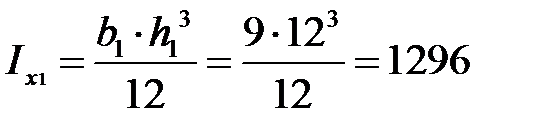см², см⁴,

см⁴.

Для 2 -го и 3 -го элементов (полукруга) получим:

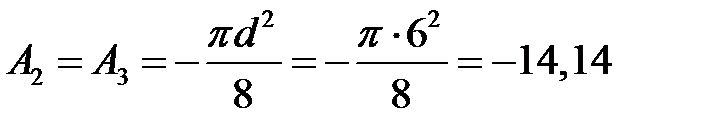см²,

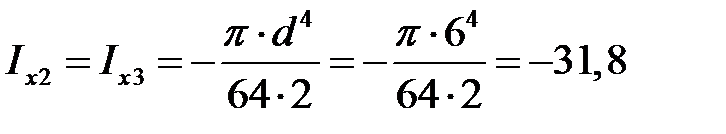см⁴,

см⁴.

Теперь по (10.7) вычислим осевые моменты инерции всего сечения. Осевой момент инерции относительно оси x _c равен

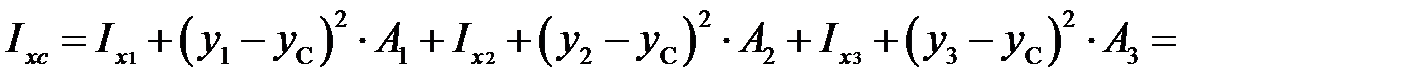
см⁴,

Осевой момент инерции относительно оси y _c

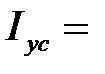
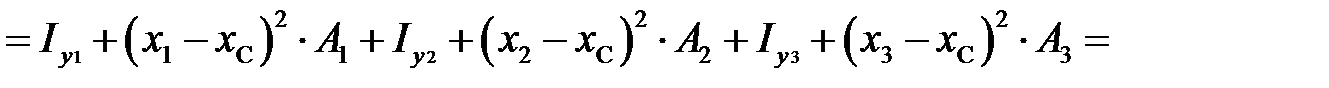
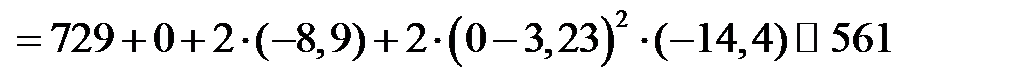см⁴.

Найденные центральные моменты инерции есть главные моменты инерции сечения. Укажем значения главных моментов инерции I _max, I _min:

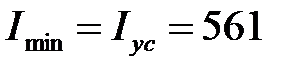см⁴, см⁴.

Потеря устойчивости происходит в плоскости минимального момента инерции I _min = 563 мм⁴, поэтому при вычислении гибкости стержня радиус инерции равен

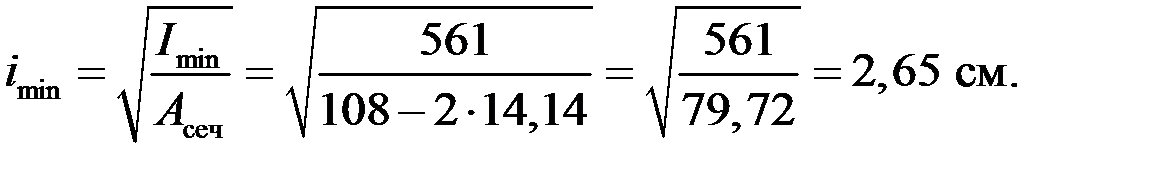
Теперь подсчитаем гибкость стержня по (10.2),

Из табл. 10.5 выписываем соотношения для 2-х ближайших значений 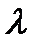(λ = 70 и λ = 80).

Имеем: при гибкости λ= 70 ¾ коэффициент φ = 0,81,

при гибкости λ = 80 ¾ коэффициент φ = 0,75.

С помощью прямой пропорции (или интерполирования) находим нужное значениекоэффициента 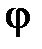для гибкости λ = 75,5, учитывая с ростом гибкости уменьшение значения :

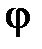Теперь найдём значение допускаемой силы по (10.6):

=

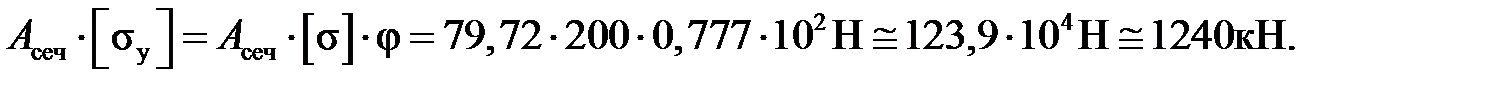
Дата добавления: 2015-06-04