Теоретические основы решения. Стержень, схема которого приведена в табл

Условие задачи

РАСЧЁТ НА УСТОЙЧИВОСТЬ ЦЕНТРАЛЬНО СЖАТОГО СТЕРЖНЯ

Стержень, схема которого приведена в табл. 10.1, сжат силой, приложенной в центре тяжести сечения. Длина l стержня, вид материала и параметры стержня σ _а, σ _b, λ₀, λ_пред из этого материала заданы в табл. 10.2.

Варианты формы и размеров поперечного сечения указаны в табл.10.3 и табл.10.4: для стального стержня из стали Ст. 3, Ст. 5 можно задать либо двутавровое сечение, либо составное сечение из простых фигур (см. табл.10.4); для стержня из дюралюминия задано кольцевое сечение (см. табл.10.3); для стержня из дерева (сосна) ̶ прямоугольное сечение (см. табл.10.3).

Требуется:

1. Определить допускаемую силу .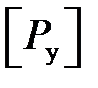

2. Найти критическое значение сжимающей критической силы 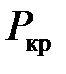и запас устойчивости по допускаемой силе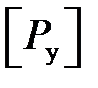

В практике часто встречаются случаи нагружения элементов продольной силой, при которых возможна потеря устойчивости. Такие элементы рассматривается как стержень под действием сжимающей продольной силы Р или, как принято говорить, рассматривается центрально сжатый стержень. Такая расчётная схема применяется при расчёте стоек оборудования, стержней механизмов, несущих колонн, стержней ферм др.

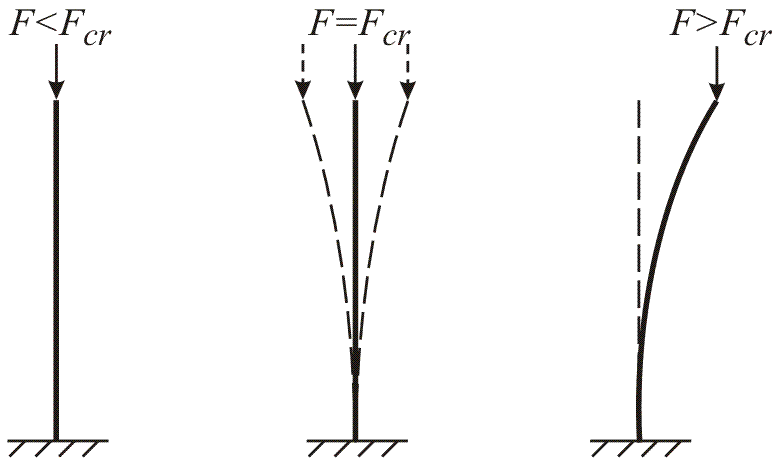
При определённом значении силы происходит внезапное искривление стержня и изменение первоначальной прямолинейной формы упругого равновесия, – это потеря устойчивости стержня (рис. 10.1, а). Значение силы называют критической Р _кр, тогда критическое напряжение в стержне равно

,

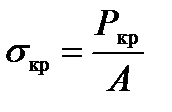где А ¾ площадь поперечного сечения стержня. Опасность потери устойчивости не только во внезапности, но и в том, что она происходит при критическом напряжении 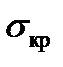, которое может оказаться существенно меньше допускаемого: .

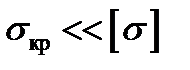Способность стержня сохранять начальную форму упругого равновесия под нагрузкой называется устойчивостью. Стержень устойчив, если сила и напряжение не превышают определённых допускаемых значений, поэтому условие устойчивости имеет вид:

,…………………(10.1)

где n _у ─ коэффициент запаса устойчивост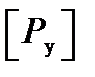и, и 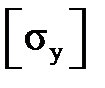─ допускаемые на устойчивость сила и напряжение.

Коэффициент запаса устойчивости зависит от назначения стержня и его материала. Так для стальных стержней, используемых в технике, , для стержней из дерева и чугуна .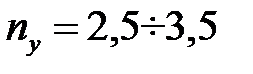

Необходимо заметить,что теряют устойчивость не только центрально-сжатые стержни, но и многие другие конструкции, расчётная схема которых совершенно другая, например, пластины и оболочки. Устойчивость – это большой раздел механики деформируемых тел.

Р кр
а	б

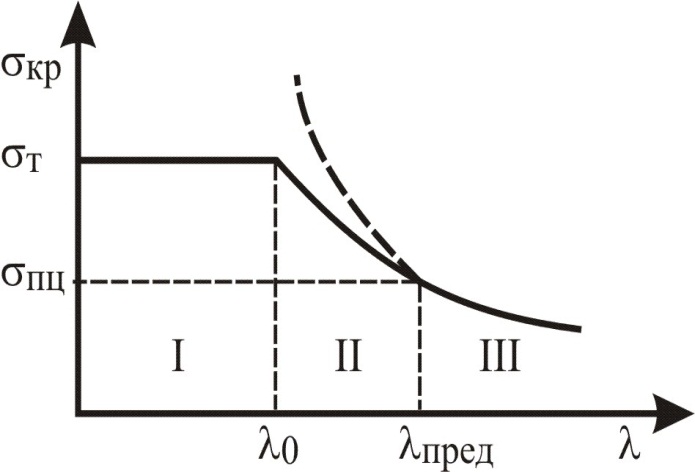
Рис. 10.1

Величина критической силы 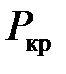для центрально сжатого стержня зависит от его важной геометрической характеристики ‒ гибкости стержня λ, значение которой определяют как

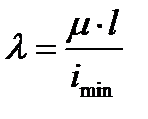, (10.2)

где 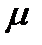– коэффициент приведения длины стержня, он указан на расчётной схеме стержня; 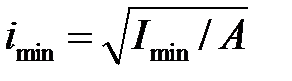– минимальный радиус инерции сечения, здесь 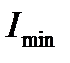– минимальный момент инерции сечения, этим учитываем, что потеря устойчивости происходит в плоскости наименьшей жёсткости, А -площадь сечения.

На рис. 10.1, б дана диаграмма критических напряжений 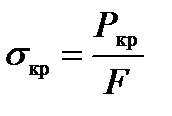, на которой прослеживается три зависимости этих напряжений от гибкости стержня, поэтому в зависимости от величины гибкости имеем три группы стержней:

III-я группа ‒ длинные;

II-я группа ‒ средние;

I-я группа ‒ короткие стержни.

Ввиду этого формула для вычисления силы 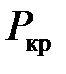выбирается в зависимости от величины гибкости λ, найденной по (10.2) для конкретного центрально-сжатого стержня.

При гибкости стержня λ, удовлетворяющей условию

λ ≥ ,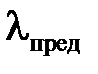

имеем длинные стержни (III-я группа). Здесь 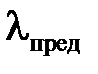‒ предельная гибкость стержня, которая зависит от свойств материала стержня. Её значение определяется как

,

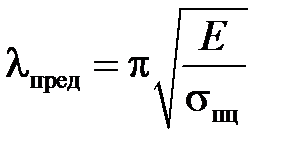где Е ‒ модуль упругости материала, σ_пц ‒ егопредел пропорциональности.

Для длинных стержней используется формула Эйлера

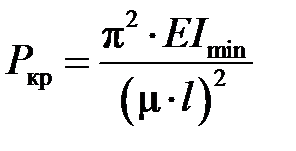. (10.3)

При гибкости стержня λ, удовлетворяющей условию

λ₀ ≤ λ ≤ λ_пред,

имеем средние стержни (II-я группа). Критическую силу 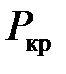для них вычисляют по эмпирической формуле Ясинского-Тетмайера

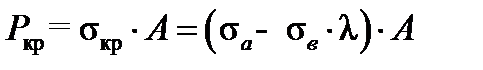. (10.4)

Значения величин Ϭ _а, Ϭ _в, 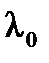и 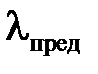нужно взять из табл.10.2, их значения получены в зависимости от вида материала и гибкости стержня.

Если гибкость стержня λ≤ λ₀,имеем короткие стержни (I-я группа), они не теряют устойчивости и рассчитываются на прочность.

Для расчётов сжатых стержней создано условие устойчивости, которое справедливо для всех трёх групп стержней. Считая, что в сечении площадью А напряжения равны 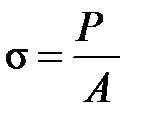, это условие устойчивости записывают в виде

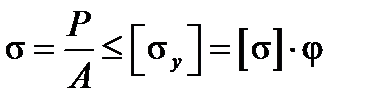, (10.5)

где 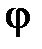- коэффициент уменьшения основного допускаемого напряжения .

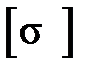Коэффициент φ ещё называют коэффициентом продольного изгиба. Он изменяется в пределах 0 ÷ 1. Значения φ для некоторых материалов приведены в табл. 10.5. Условие (10.5) называют условием устойчивости по коэффициенту уменьшения основного допускаемого напряжения 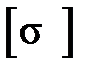, или условием устойчивости по коэффициенту .

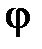Дата добавления: 2015-06-04