Корреляция бисериальная

(лат. bis series — два ряда, две серии) — метод корреляционного анализа отноше­ния переменных, одна из которых измере­на в дихотомической шкале наименова­ний, а другая — в интервальной шкале отношений или порядковой шкале. Назва­ние метода связано с тем, что сравнивают­ся две альтернативные серии объектов X, имеющие условные значения 0 или 1 по Y.

Наиболее характерно применение ко­эффициентов К. б. в психологической диагностике при анализе дискримина-тивности заданий теста, а также при определении валидности критериаль­ной путем коррелирования значений тес­товых оценок с независимыми характе­ристиками критерия, выраженными в ди­хотомической шкале (см. Шкалы изме­рительные).

Для описания связи между перечис­ленными видами переменных исполь­зуется точечный бисериальный коэффи­циент корреляции Пирсона:

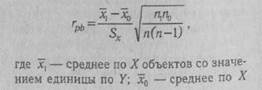
объектов со значением нуль по У; S_x — стандартное отклонение всех значений по X; rtj — число объектов, с единицей по У: щ — число объектов с нулем по У, т. е. п = П[ + п₀. Уравнение для вычисления г_рЬ представляет собой алгебраическое упрощение формулы коэффициента г_ху (см. Корреляционный анализ) для слу­чая, когда У— дихотомическая перемен­ная. Можно привести ряд других эквива­лентных выражений, удобных для прак­тического применения:

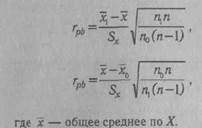
Значение г_рЬ варьирует от -1 до +1. В том случае, когда переменные с единицей по Y имеют среднее по X, равное средне­му переменных с нулем по У, г_рЬ обраща­ется в нуль.

В качестве примера можно привести вычисление г _ь при анализе дискримина-тивностн отдельных пунктов опросника личностного, т. е. корреляции между ти­пичным ответом на отдельный пункт (ут­верждение—отрицание) с общим резуль­татом по тесту (табл. 10).

Вычисленное таким образом значение г_рЬ показывает, что проверяемый пункт опросника имеет среднюю диагностичес­кую значимость и слабо коррелирует с об­щим результатом теста.

Достоверность (а) связи, рассчитан­ной с помощью коэффициента г_рЬ, может определяться с помощью критерия Я² для числа степеней свободы df = 2.

Другим распространенным методом расчета является определение бисериаль-ного коэффициента корреляции (г_ш), ко­торый применяется в тех случаях, когда

есть основания полагать, что дихотоми­ческое распределение близко к нормаль­ному:

Элементы уравнения идентичны ис­пользуемым при вычислении г_рЬ, за исключением величины U — ординаты

Таблица 10

Вычисление точечного бисериального ко­эффициента корреляции Пирсона

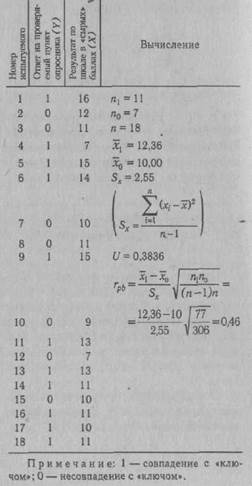
КОРРЕЛЯЦИЯ КАЧЕСТВЕННЫХ ПРИЗНАКОВ — метод анализа связи переменных, измеряемых в порядковых шкалах и шкалах наименований (см. Шкалы измерительные). Наиболее час-го такой корреляционный анализ прово­дят с помощью коэффициентов корреля­ции ранговой, используемых в случаях, когда обе переменные измеряются ег шка­лах порядка или легко могут быть преоб­разованы в ранги. При измерении сравни­ваемых переменных в шкалах наименова­ний широко применяются коэффициенты сопряженности, в которых в качестве про­межуточной расчетной величины исполь­зуется критерий согласия Пирсона (см. Критерий X²). Наиболее часто в таких расчетах пользуются коэффициентом со­пряженности Пирсона:

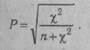
Значение Р всегда положительно и из­меряется от нуля до единицы. Особеннос­тью коэффициента сопряженности Пир­сона является то, что максимальное его значение всегда меньше +1 и в значитель­ной степени зависит от количества на­блюдений (размера таблицы). В случае квадратной таблицы (k x k)

где t — число столбцов таблицы, k — чис­ло строк таблицы.

В психологической диагностике опи­санные коэффициенты используются от­носительно редко.

КОРРЕЛЯЦИЯ РАНГОВАЯ — метод корреляционного анализа, отражающий отношения переменных, упорядоченных по возрастанию их значения. Наиболее часто К. р. применяется для анализа свя­зи между признаками, измеряемыми в по­рядковых шкалах (см. Шкалы измери­тельные), а также как один из методов определения корреляции качественных признаков. Достоинством коэффициен­тов К. р. является возможность их ис­пользования независимо от характера распределения коррелирующих призна­ков.

В практике наиболее часто применя­ются такие ранговые меры связи, как ко­эффициенты К. р. Спирмена и Кендалла. Первым этапом расчета коэффициентов К. р. является ранжирование рядов пере­менных. Процедура ранжирования начи­нается с расположения переменных по возрастанию их значений. Разным значе­ниям присваиваются ранги, обозначае­мые натуральными числами. Если встре­чаются несколько равных по значению пе­ременных, им присваивается усреднен­ный ранг (табл. 12).

В табл. 13 приведены данные для рас­чета коэффициентов К. р. Во второй гра­фе представлены ранжированные пока­затели по первому из сравниваемых рас­пределений (оценка IQ, в третьей гра­фе — соответствующие им данные теста зрительной памяти-).

Коэффициент корреляции рангов Спирмена (r_s) определяется из уравне­ния:

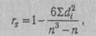
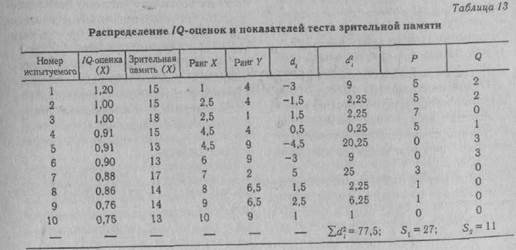
ент х более информативен, чем r_s, и рас­считывается проще. Поэтому на практике при расчете К. р. отдают предпочтение ко­эффициенту т.

КОСА КУБИКИ — невербальный тест интеллекта. Предложен К. Косом в 1920 г.

Испытуемому предлагают составить фигуры из цветных кубиков по рисункам-образцам. Тестовый материал состоит из шестнадцати кубиков с ребром 2,5 см, сто­роны которых окрашены в красный, бе­лый, желтый и синий цвета. Оставшиеся две противоположные грани разделены по диагонали, причем одна окрашена в белый и красный цвета, а вторая — в синий и желтый (см. Векслера интеллекта из­мерения шкалы, рис. 13). В набор вклю­чены восемнадцать образцов фигур, пер­вый из которых является тренировочным и выполняется совместно с испытуемым. Цвета рисунков-образцов соответствуют цветам кубиков, но размеры образцов вдвое меньше. Образцы размещены посе­редине картонной карточки, имеющей размер 10 х 7,5 см.

Задания следуют в порядке возраста­ющей трудности, что обеспечивается пос­ледовательной комбинацией следующих условий:

— фигуру можно построить только из од­ноцветных сторон кубиков;

— для построения фигуры следует ис­пользовать несколько двухцветных граней;

— фигуру можно сложить только из двухцветных сторон или из сочетания двухцветных и одноцветных, причем на образце не обозначена граница между соседними кубиками;

— образец повернут на 45°, т. е. стоит на ребре;

— для составления фигур требуется ис­пользовать все большее количество кубиков;

— образцы постепенно становятся все менее симметричными;

— увеличивается количество цветов на образце;

— образец не ограничивается рамкой, так что на краях сливается с фоном. Образцы-рисунки испытуемому предъ­являются последовательно,тестирование прекращается после пяти последовавших друг за другом неудачных решений. Ус­пешность оценивается с нескольких пози­ций. Самым важным показателем явля­ется время решения отдельных заданий. В протоколе фиксируется и количество попыток при выполнении. Первичные оценки по результатам выполнения зада­ний переводятся в показатель умствен­ного возраста. В более поздних модифи­кациях оценки переводятся в IQ-показа-тели стандартные. Данные дополняют­ся качественным анализом поведения ис­пытуемого.

К. к. принадлежат к часто применяе­мым тестам и широко используются как в оригинальной, так и в сокращенных моди­фикациях (см., напр., Векслера интел­лекта измерения шкалы). Ценность те­ста определяется особенностями деятель­ности испытуемого, которая моделирует- -ся его заданиями. Испытуемый начинает выполнение задания с анализа образца, путем сопоставления фрагментов образца с гранями кубиков. Затем осуществляет­ся генерализация выделяемого признака. Вслед за этим осуществляется переход к синтезу—констатация соответствия между образцом и собранной из кубиков фигурой. По мнению К. Коса, в ходе реше­ния заданий задействуются все мысли­тельные процессы.

Имеются сведения о валидности кон-структной К. к. Получена значимая кор­реляция с Вине—Симона умственного развития шкалой (г = 0,82 у нормаль­ных детей и г = 0,67 у слабоумных детей). Изучались связи показателей К. к. с

основными тестами интеллекта, в частно­сти Станфорд—Бине умственного раз­вития шкалой (г = 0,77), Равена про­грессивными матрицами (г = 0,81). Об­ращается внимание на независимость друг от друга показателей К. к. и тестов арифметических способностей.

Наиболее широкое применение К. к. находят в клинической психодиагностике (В. М. Блейхер, И. В. Крук, 1986). По данным Л. Кошча (1976), тест весьма по­лезен при работе с такими разнообразны­ми контингентами испытуемых, как твор­ческие личности с высоким уровнем спо­собностей и, с другой стороны, умствен­но отсталые лица; дети с минимальной мозговой дисфункцией, нарушением кон­центрации внимания, нарушением про­странственной ориентировки; дети, стра­дающие неврозами; дети с задержкой психического развития, педагогически за­пущенные; больные юношеского и зрело­го возраста, страдающие шизофренией. Тест может использоваться и при анали­зе интеллектуального потенциала здоро­вых лиц.

В отечественной психодиагностике К. к. используются чаще всего в том виде, как они представлены в соответствующем отдельно взятом субтесте Векслера ин­теллекта измерения шкалы.

КОЭФФИЦИЕНТ АЛЬФА (а) — ста

тистический показатель, используемый при дисперсионном анализе. Предложен Л. Кронбахом (1971). Наиболее часто при­меняется при оценке надежности теста. Уравнение К. А. имеет следующий вид:

дартных отклонений для отдельных зада­ний. В том случае, если в методике при­меняются задания дихотомического типа («да»—«нет», «правильно»—«неправиль­но»), может быть использована упрощен­ная формула:

где п — количество заданий теста, а;² — квадрат стандартного отклонения для все­го теста, Zct,-² — сумма квадратов стан-

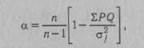
где SPQ = Xcy и Р — доля испытуемых, давших «ключевой» или правильный от­вет, а Q = 1 - Р. Дихотомический вариант К. А. является уравнением Кьюдера—Ри­чардсона (см. Надежность частей тес­та). Применение К. А. основано на моде­ли, предполагающей наличие большой дисперсии (а стало быть, и дискримина-тивности заданий теста) скорее у надеж­ного, чем у ненадежного теста (см. На­дежность факторно-дисперсионная). Таким образом, если при факторном анализе возвести в квадрат и просумми­ровать нагрузки выявленных факторов, можно определить надежность, поскольку нагрузки факторов представляют корре­ляцию теста с общими или специфически­ми факторами. Модель надежности фак­торно-дисперсионной близка к анализу надежности по внутренней согласо­ванности.

Факторно-дисперсионный метод ана­лиза надежности находится в сильной за­висимости от выбора переменных, в свя­зи с которыми факторизуется тест. Так, если сопоставлять тест математических способностей с личностными или мотива-ционными переменными, то оценка на­дежности была бы неадекватной (практи­чески не было бы общих факторов). С дру­гой стороны, если бы тест факторизиро-вался совместно с тестами общих способ­ностей так, чтобы каждый тест мог нагру­жать соответствующие ему факторы, ме­тод надежности факторно-дисперсионной

мог бы быть достаточно точным. Таким об­разом, эта модель подходит для оценки на­дежности теста, факторная валидность которого известна или задана прн разра­ботке, а также тестов, связанных с огра­ниченным числом общих факторов.

КРИТЕРИАЛЬНО-КЛЮЧЕВОЙ ПРИНЦИП — принцип конструирова­ния тестов на основе обнаружения (эмпи­рического) психологических признаков, позволяющих дифференцировать реле­вантные критериальные группы от конт­рольных. Широко используется для кон­струирования психодиагностических ме­тодик наряду с факторно-аналитическим принципом. Примером методик, в кото­рых реализован К.-к. п., являются опрос­ники эмпирические, такие как Минне-сотский многоаспектный личностный опросник, «Бланк интересов» Стронга (см. Опросники интересов) и др.

Так, при разработке MMPI из первона­чального банка утверждений в основные клинические шкалы включались только те, которые хорошо дифференцировали испытуемых с тем или иным клиническим диагнозом от контрольной группы здоро­вых людей (см. Дискриминативность заданий теста). В шкалы «Бланка инте­ресов» Стронга вошли те утверждения из первоначального набора, которые реально разделяли группы лиц, являвшихся носи­телями определенных интересов. Иногда задания, объединенные общей шкалой в силу эмпиричности конструирования, не имеют не только теоретического, но даже интуитивного, гипотетического объясне­ния.

В тех случаях, когда необходимо диск­риминировать группы, напр., в профотбо­ре, К.-к. п. является достаточно эффек­тивным.

В тестах, созданных в соответствии с К.-к. п., основное значение придается дис-криминативности. Важен тот факт, что

тест является дискриминативным, а не причина, по которой это происходит. В связи с использованием К.-к. п. конструи­рования тестов возникает ряд проблем, которые должен решать разработчик. К их числу в первую очередь следует отнести трудности в отборе критериальных групп. MMPI, например, разрабатывался, как указывалось выше, путем сопоставления больных и здоровых, однако- разработка шкалы шизофрении (S_c) или паранойи (Р_&) с большим успехом могла бы опирать­ся на сопоставление группы больных с вы­раженными шизоидными или паранойяль­ными тенденциями с группой пациентов, у которых отмечаются противоположные патологические особенности, но это прак­тически нереально. Комплектование кри­териальной группы больных опиралось на врачебный диагноз, который разными спе­циалистами может восприниматься по-разному. Сложность в отборе «чистых» групп для сравнения ведет, в конечном итоге к снижению надежности и валид-ности теста. (См. также Контрастные группы.)

Другая проблема связана со значи­тельными трудностями, а иногда и невоз­можностью психологической интерпрета- ■ ции показателей тестов, созданных в соответствии с К.-к. п. Наиболее вероят­ным является то, что одна критериальная группа отличается от релевантной ей не одним, а несколькими (иногда многими) переменными. Полученные шкалы явля­ются, таким образом, не однозначными, а мультивариантными. Следовательно, два идентичных показателя могут иметь раз­личную интерпретацию, и не существует определенного способа-по виду показате­ля установить, что измеряет данная шка­ла. Факт, что тест может дискриминиро­вать группу X от группы У, не говорит ничего о природе переменной, измеряе­мой тестом, если только мы не располага­ем доказательством, что группы отлича-

ются одна от другой лишь по одной пере­менной.

Результатам тестов, разработанных на основе К.-к. п., присуща известная специ­фичность, что также является серьезным ограничением. Например, если такой тест используется для.отбора сборщиков элек­тронной аппаратуры, он будет разрабаты­ваться на основе конкретного критерия, связанного с выполнением работы опре­деленного характера. Если содержание работы изменится, разработанный на ос­нове неадекватных критериальных при­знаков тест станет бесполезен. В противо­вес этому тесты, ориентированные на ба­зовые способности, по-прежнему могут быть использованы.

Факторный тест, относительно «чис­тый» по исследуемым переменным и опирающийся на теорию измеряемого конструкта, как можно ожидать, будет предпочтительней страдающих эмпирич­ностью тестов, созданных в соответствии с К.-к. п. Однако разработка факторно-аналитического теста является техничес­ки более сложной, трудоемкой задачей.

Не нужно противопоставлять К.-к. п. конструирования тестов факторно-анали­тическому принципу; следует помнить, что при подборе первичного банка зада­ний разработчики исходят, как правило, из описания некоего свойства, конструк­та, являющегося объектом измерения. С другой стороны, разработанный по К.-к. п. тест в последующем может пройти проце­дуру факторизации.

«Эмпиричность* таких тестов в значи­тельной степени сглаживается и последу­ющей процедурой определения валидное-ти конструктной.

Для методик, созданных в соответ­ствии с К.-к. п., наибольшее значение име­ют эмпирические модели определения на­дежности (см. Надежность ретестовая, Надежность параллельных форм, На­дежность частей теста).

КРИТЕРИЙ X² (критерий согласия Пир­сона) — характеристика распределения, используемая для проверки статистичес­ких гипотез. Под статистическим крите­рием подразумевается правило, обеспечи­вающее с определенной вероятностью принятие истинной или отклонение лож­ной гипотезы. В качестве критериев в математической статистике применяют определенные случайные величины, явля­ющиеся функциями изучаемых случай­ных величин и чисел степеней свободы. Одним из наиболее часто применяе­мых является К. X², представляющий со­бой сумму квадратов отклонений эмпири­ческих частот (р) от теоретических или ожидаемых (p')_t отнесенную к теоретиче­ским частотам:

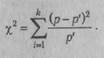
При полном совпадении эмпирических и ожидаемых частот S (р - р') = 0. При несовпадении производится сравнение эмпирической величины X² с его крити­ческим значением, определенным по таб­лицам (см. Приложение III, табл. 3). Ну­левая гипотеза, которая предполагает, что расхождение между эмпирическими частотами и математическим ожиданием носит случайный характер и между вы­численными и эмпирическими частотами разницы нет, опровергается, если X² £ Х²_Р для принятого уровня значимости (а) и числа степеней свободы (df). В качестве примера проанализируем с помощью К. X распределение частот выбора ответа на закрытый пункт теста (см. Задачи закры­того типа). Предлагаемые варианты не­правильных ответов должны быть при­мерно равновероятны. При обследовании 100 человек, отвечающих на проверяемый пункт неверно, результаты распредели­лись следующим образом (табл. 14).

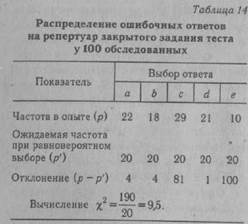
Степень свободы для данного случая df = п - I =4 (где п — число вариантов ответа). По табл. 3 Приложения III для а = 0,01 и df ~ 4 находим Х²_кр = 3,28. По­лученное значение X² = 9,5 меньше таб­личного. Следовательно, при решении за­дачи может быть принята гипотеза о примерно равновероятном распределении выбора ответов а, Ь, с, d, e. При повтор­ных случайных выборках вероятность ложного вывода составит 1 %.

В качестве другого примера рассмот­рим проверку нормальности распределе­ния тестовых оценок (см. Оценка типа распределения). Исходные данные приве­дены в табл. 15, 16.

Число степеней свободы определяется в данном случае исходя из свойств нор­мального распределения df=k—§ (ог­раничения свободы вариации х, S_x, n). В результате объединения частот в крайних классах (см. ниже) число классов сокра­тилось с 9 до 7, тогда df = 4. По таблице критических значений X² для а = 0,05 на­ходим %²_кр в 9,49, X² < %²_кр, следовательно, распределение тестовых оценок идет по нормальному закону, расхождения между эмпирическим и нормальным распределе­нием случайны и несущественны.

Как видно из данного примера, для проверки гипотезы о законе распределе-

ния необходимо сопоставить эмпиричес­кие и расчетные теоретические частоты. Последние рассчитываются на основании эмпирических данных по формулам, опи­сывающим тот или иной закон распреде-

ления вероятностей. Так, для проверки нормальности распределения теоретиче­ские частоты рассчитываются по фор­муле:

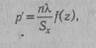
где п_х и я₂ — объемы сравниваемых выбо­рок, р_{н р₂ — частоты первого и второго рядов. Нулевая гипотеза сводится к тому, что сравниваемые выборки взяты из од­ной и той же совокупности генеральной и, следовательно, несовпадение между ча­стотами Р] и р₂ носит случайный харак­тер.

К. X² обычно используется для провер­ки гипотез о соответствии (согласии) эм­пирического распределения теоретичес­кому (см. приведенные выше примеры); при проверке гипотез о статистической независимости признаков (при Х²>Х^_р предложение об отсутствии связи между признаками отвергается). Теснота связи может быть рассчитана с помощью коэф­фициента сопряженности Пирсона (см. Корреляция качественных признаков), при подтверждении гипотезы об однород­ности распределения признаков в разных совокупностях (в этом случае нулевая ги^: потеза формулируется как предположе­ние о сходстве распределения признака в двух совокупностях генеральных, из кото­рых взяты независимые выборки объема­ми п_ и nj:

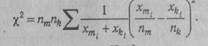
Преимуществами К. X* являются при­менимость его для различных распределе­ний дискретных и непрерывных призна­ков, необязательность предварительных сведений о законе распределения изучае­мой переменной. При использовании К. X² следует учитывать такие ограничения:

— сравниваемые выборки должны быть получены из независимых наблюде­ний;

— минимальное значение эмпирической частоты не должно быть менее 10, те­оретической — менее 5. Если это тре­бование не выполняется, необходимо увеличить объем выборки или объеди­нить интервалы группировки, сумми­руя их частоты (см, выше пример срав­нения эмпирического и нормального распределения).

КРОУНА—МАРЛОУ СОЦИАЛЬНОЙ ЖЕЛАТЕЛЬНОСТИ ШКАЛА (Crow-ne—Marlowe Social Desirability Scale, CM SDS) — опросник личностный. Разрабо-

тан Д. Кроуном и Д. Марлоу в 1960 г. для диагностики мотивации одобрения.

К.—М. с. ж. ш. состоит из 33 утверж­дений (18 социально одобряемых и 15 со­циально неодобряемых образцов поведе­ния), с каждым из которых испытуемый должен выразить, согласие или несогла­сие. Примеры утверждений (из русско­язычного варианта): 1. Я внимательно читаю каждый доку­мент, прежде чем его подписать; 7. Иногда я люблю позлословить об от­сутствующих;

17. Были случаи, когда я завидовал уда­че других.

Каждый ответ, совпадающий с клю­чом, оценивается в 1 балл. Итоговый по­казатель мотивации одобрения получают суммированием всех баллов. Этот пока­затель характеризует мотивационную структуру субъекта и, в частности, сте­пень его зависимости от благоприятных оценок со стороны других людей, его ра­нимость и чувствительность к средовым и межличностным влияниям. Иными слова­ми, шкала позволяет получить косвенную меру потребности человека в одобрении со стороны других людей,

Авторы шкалы руководствовались стремлением разработать инструмент, свободный от известной фиксированнос-ти на патологических симптомах, что в той или иной степени присуще ранее со­зданным шкалам (см. Шкалы конт­рольные). Кроме того, была поставлена задача дифференциации содержания ут­верждений от влияния собственно моти­вов.. Имеются данные о достаточно высо­кой валидности и надежности К.—М. с. ж. ш.

В СНГ известен русскоязычный сокра­щенный вариант шкалы (20 утвержде­ний), стандартизированный на выборке более 800 человек с последующей провер­кой валидности и надежности (Ю. Л. Ха-нин, 1974, 1976). Шкала применяется:

при исследовании мотивации одобрения; для контроля за степенью установочного поведения и склонностью к соответству­ющим искажениям ответов в тестах (см. Установки на ответ); при изучении предпочтительных средовых и межлично­стных влияний.

КРУГОЗОРА И ИНФОРМИРОВАН­НОСТИ ТЕСТ — вербальный тест ин­теллекта, предназначенный для оценки общей осведомленности детей. Разрабо­тан Й. Йирасеком в 1953 г.

Материал теста состоит из 40 вопро­сов, расположенных в порядке возраста­ния трудности, В зависимости от полноты ответа выставляется оценка 2, 1 или О баллов. Первичные баллы с помощью таб­лиц переводятся в показатели IQ для воз­растных групп от 8 до 13,6 года.

Автор приводит следующие данные о психометрических свойствах теста:

— валидность конструктная, опреде­ленная корреляцией со Станфорд— Вине шкалой умственного разви­тия, имеет значение г = 0,76.

— надежность частей теста г = 0,96,

— показатель- внутренней согласован­ности г = 0,67.

— валидность содержательная обес­печена отбором тестовых заданий из первоначального состава в 60 во­просов.

Тест может найти применение в школьной и клинической психодиагнос­тике как скрининговая методика (см. Отсеивание).

Данных об использовании в СНГ не имеется.

КУДЛИЧКОВОЙ ЛИЧНОСТНЫЙ ОПРОСНИК (КУД) — опросник лично­стный. Разработан Е. Кудличковой в 1964 г.

Опросник содержит 80 вопросов, на которые испытуемые могут отвечать:

«согласен», «не знаю», «не согласен*. При­меним для взрослой популяции без огра­ничения возраста, допускает как индиви­дуальное, так и групповое обследование. На основании оценки первичной испыту­емых размещают на девятибалльной шка­ле станайнов (см. Оценки шкальные).

Диагностика опирается на анализ пяти биполярных факторов личности: устойчи­вость—лабильность, активность—пас­сивность, доминантность—подчинен­ность, рациональность—чувствитель­ность, экстра—интроверсия. Перечислен­ные факторы, по мнению автора, включа­ют следующие свойства (в скобках приве­дены примеры вопросов, диагностирую-щих соответствующие факторы):

— Активность: быстрота реакций, ре­шительность, динамичность (Бывает, что я никак не могу принять какое-то решение и упускаю возможность сде­лать что-либо своевременно),

— Пассивность: медлительность, нере­шительность, отсутствие напористос­ти (Чаще всего я стараюсь действовать так, чтобы «не напороться на какие-ли­бо неприятности»).

— Лабильность: возбудимость, неурав­новешенность, беспокойство, импуль­сивность (Обычно я ничего не плани­рую, действую -по настроению в данный момент).

— Стабильность: уравновешенность, рассудительность, владение собой, по­стоянство (Я сохраняю спокойствие даже тогда, когда другие люди теряют самообладание).

— Доминантность: властность, само­уверенность, авторитарность, агрес­сивность (С удовольствием выступаю в роли организатора).

— Подчиненность: несамостоятель­ность, покорность, терпимость (В кол­лективе, компании других людей я легко поддаюсь уговорам, проявляю покладистость).

— Рациональность: рефлексивность, объективность, рассудительность (Я высказываю свои мысли, тщатель­но подумав, стремлюсь выразить их как можно точнее).

— Чувствительность: богатое вообра­жение, интуиция, непосредствен­ность, субъективизм (Я обычно при­даю важное значение внешнему виду и одежде людей — обращаю внимание, одеты ли они по моде, смотрю на каче­ство ткани).

— Экстраверсия: кооперативность, об­щительность, открытость, социабель-ность, разговорчивость (Я был бы очень огорчен, если бы длительное время не мог встречаться со своими знакомыми, друзьями).

— Интроверсия: замкнутость, сдержан­ность, внешняя холодность (Чтение книг доставляет мне больше удоволь-

' ствия, чем встречи и беседы со знако­мыми и приятелями). В процессе психометрической разра­ботки опросника особое внимание уделя­лось валидности содержательной ут­верждений. Устанавливалась внутрен­няя согласованность, а также дискрими-нативность отдельных утверждений. В окончательную версию К. л. о. были включены только те утверждения, кото­рые соответствовали статистическим кри­териям, однако точные данные в руковод­стве не приведены. Имеются сведения о надежности ретестовой {r_t = 0,80 -- 0,96). Нормы в станайнах разработаны автором для ограниченного контингента испытуемых (студентов, аспирантов ву­зов, женщин и мужчин, занимающих ру­ководящие должности, рабочих отдель­ных специальностей, работников здраво­охранения). Допускается как индивиду­альное, так и групповое обследование.

Опросник рекомендуется для диагнос­тики личности, однако примитивность стандартизации, условность норм, от-

сутствие сведений о валидности конст-руктной и валидности критериальной делают его скорее средством для получе­ния ориентировочной, предварительной информации.

Сведений об использовании в СНГ нет.

КУКОЛ ТЕСТ (Puppetry Test) — проек­тивная методика исследования лич­ности, разрабатывалась А. Вольтманом (1951), М. Гауорт (1957) и другими пси­хологами. Ранее процедуры, близкие К. т., использовались психоаналитически ори­ентированными исследователями как те­рапевтическая техника для детей в возра­сте до 10 лет (М. Рамберт, 1938).

Стимульный материал методики пред­ставлен куклами, число которых у разных авторов не совпадает. Ребенка просят ра­зыграть с куклами различные сцены, напр, соперничество с братом, сестрой или ситуации с участием отца, матери, других близких. Иногда детям предлагают поставить кукольное представление. Та­кая организация исследования под руко­водством экспериментатора-режиссера сближает К. т. с психодрамой. Процедура обследования не стандартизована. Отсут­ствует система оценки полученных дан­ных, не разработана схема интерпрета­ции. Упор делается на интуицию иссле­дователя. Попытки стандартизации К. т. предприняты М, Гауорт, создавшей фильм — кукольное представление, одна­ко данные о валидности и надежности теста отсутствуют.

Сведений об использовании в СНГ не имеется.

КУЛЬТУРНО-СВОБОДНЫЙ ИН­ТЕЛЛЕКТА ТЕСТ (Culture-Fair Intel­ligence Test, CFIT) — тест интеллек­та. Предназначен для измерения уровня интеллектуального развития, независи­мого от влияния факторов окружающей среды (культуры, образования и т.д.),

т. н. «чистого» интеллекта. Опубликован Р. Кэттеллом в 1958 г. Имеется три вари­анта теста; а) для детей 4-8 лет и ум­ственно отсталых взрослых; б) для детей 8-12 лет и взрослых, не имеющих высше­го образования (две параллельные формы А и В); в) для учащихся старших классов, студентов и взрослых с высшим образова­нием (две параллельные формы А и В).

Первый вариант теста состоит из вось­ми субтестов, четыре из которых рассмат­риваются автором в качестве «свободных от влияния культуры»: 1) «подстановка»; 2) «классификация»; 3) «выбор называе­мых предметов»; 4^ «лабиринты»; 5) «кар­тинки с недостающими деталями»; 6) «вы­полнение указаний»; 7) «загадки»; 8) «определение сходства». Время реше­ния всех заданий — 22 мин.

Второй и третий варианты К.-с. и. т. состоят из четырех субтестов и отличают­ся лишь уровнем трудности (рис. 34): «Се­рии» — распознание и продолжение за­кономерных изменений в рядах фигур; «Классификация* — определение общих черт, особенностей фигур; «Матрицы» — дополнения к комплектам фигур; «Усло­вия» — перестановка фигур, первона­чально расположенных в определенном порядке (требуется отметить точкой один из данных на выбор рисунков с соблюде­нием условий, заданных по образцу). Вре­мя, отводимое на решение всех зада­ний, — 12,5 мин. К.-с. и. т. представляет собой тест скорости, но может быть ис­пользован и без ограничения времени вы­полнения. Исходные оценки по второму и третьему вариантам теста с помощью таб­лиц преобразуются в процентили (см. Оценки шкальные) и lQ-показатель стандартный с а = 16. Первый вариант обрабатывается только посредством отно­сительного IQ (см. Интеллекта коэффи­циент).

Р. Кэттелл исходит из того, что изда­ние теста для измерения общих способно-

Тест 1. «Серии»

Выбрать недостающий квадрат:

Тест 2. «Классификация»

Выделить не относящийся к ряду элемент:

Тест 3. «Матрицы»

Найти элемент, завершающий данную матрицу.

Тест 4.«Условия»

Отметить точкой один из данных на вы­бор рисунков так, чтобы соблюсти усло­вие, заданное в образце:

Рис. 34. Образцы заданий из субтеста Культур­но-свободного интеллекта теста

стей, очищенных от «наслоений культу­ры», возможно прежде всего на основе перцептивных заданий, в- которых интел­лект проявляется через восприятие.

По мнению Р. Кэттелла, данные, полу­ченные с помощью К.-с. и. т. в различных культурных группах, вполне сопоставимы между собой. (Критику концепции'«чис­того» интеллекта см. в статье Тесты ин­теллекта).

Стандартизация К.-с. и. т. не завер­шена. Коэффициент надежности мето­дом расщепления теста (см. Надежность частей теста) составляет 0,70-0,92. Валидность изучалась путем корреляции с результатами других тестов интеллекта. По данным Р. Кэттелла, показатель корре­ляции К.-с. и. т. со Станфорд—Бине ум-

ственного развития шкалой равен 0,56. Некоторые из субтестов первого вариан­та требуют исключительно индивиду­ального предъявления, другие варианты могут использоваться как при индиви­дуальном, так и при групповом тестиро­вании.

Сведений об использовании в СНГ не имеется.

Q-КЛАССИФИКАЦИЯ (Q-sort) — ме

тодика исследования представления о своем «Я» и об окружающих людях. Пред­ложена В. Стефенсоном в 1953 г.

Выполнение заданий Q-к. состоит в сортировке карточек с названиями свойств или особенностей личности на группы в зависимости от близости данно­го свойства характеру и образцам поведе­ния обследуемого. Карточки делятся на заданное количество групп от «наиболее характерных» к «наименее характерным» для испытуемого свойствам. Обследуе­мый должен в каждой группе разместить определенное их число. Количество кар­точек в группе определяется значениями нормального распределения для выбран­ного числа групп и его общего количе­ства. Так, при количестве карточек, рав­ном 100, количестве групп — 6, распреде­ление карточек по группам может выгля­деть следующим образом:

Наименее Наиболее

характерное характерное

свойство 3 15 32 31 15 3 свойство

Наиболее удобно разделение карточек на 9 групп. При этом для определения числа карточек в каждой из групп можно воспользоваться шкалой станайнов (см. Оценки шкальные).

По характеру выполнения Q-к. отно­сится к методикам вынужденного выбора. Выраженность личностных свойств здесь измеряется не в абсолютных показателях (напр., отношение к результату норматив-

ной выборки), а относительно выраженно­сти других свойств испытуемого.

После выполнения основного задания Q-к. испытуемому можно предложить вы­полнить аналогичную сортировку приме­нительно к другим людям (отцу, матери, жене и т. д.). Существует вариант выпол­нения задания по отношению к себе или другим людям в различных ситуациях (дома, на работе, в общении и т. д.). Мож­но получить сведения относительно пред­ставления о себе в аспекте «идеального Я», «реального Я», «социального Я» (т. е. такого, каким видят испытуемого окружа­ющие) (см. Семантический дифферен­циал).

При изучении валидности проек­тивных методик Q-к. может с успехом

применяться как для получения критерия (см. Валидность критериальная, Вали-дизации критерий), так и сопоставимых с ним оценок теста. По мнению А. Анас-тази (1982), Q-к. можно использовать пос­ледовательно на разных стадиях психо­терапии для констатации изменений в психическом состоянии. При эффектив­ном терапевтическом воздействии пред­ставление о себе меняется в сторону более благоприятных оценок и приближа­ется к идеальному «Я». Методика Q-к, мо­жет найти применение в самых различных областях психологической диагностики. Принцип Q-к. может быть реализован при работе испытуемого с различными объек­тами и использован для широкого круга тестовых методик.

Дата добавления: 2015-06-04