Записать матрицу тензора напряжений. Вычислить касательные напряжения на координатных площадках

Введение

В механику сплошной среды можно условно разделить на пять основ: математически, геометрические, кинематические, динамические и физические основы. Теория напряжений – динамические основы механики сплошной среды.

Напряжение характеризует прочность тела в точке, поэтому его изучение важно, ведь разрушение тела начинается именно в точке и называется трещиной. Зная закон распределения по сечению напряжений, можно найти компоненты внутренних сил, а значит рассчитать деформации, вызываемые ими.

Теории напряжений и деформаций были созданы О.Коши. Они изложены в работе, представленной в Парижскую академию наук в 1822 г., краткое содержание которой опубликовано в 1823 г. и ряде последующих статей. О.Коши вывел три уравнения равновесия элементарного четырехгранника, доказал закон парности касательных напряжений, ввел понятия главных осей и главных напряжений и вывел дифференциальные уравнения равновесия. Им же введена поверхность нормальных напряжений (квадрика Коши), на которой располагаются концы радиус-векторов, направления которых совпадают с направлением нормалей к площадкам, а величина обратно пропорциональна корню квадратному из абсолютной величины нормального напряжения в этой площадке, и доказано, что эта поверхность является поверхностью второго порядка с центром в начале координат. Возможность преобразования поверхности нормальных напряжений к главным осям свидетельствует о существовании в каждой точке трех взаимно главных перпендикулярных площадок.

Большой вклад в развитие механики сплошной среды и теории пластичности внесли и советские ученые. Следует отметить труды С.Л. Соболева, С.А. Христиановича, Л.И. Седова, А.А. Ильюшина.

Цель данной работы - закрепить, расширить и углубить полученные знания по теории напряжений, приобрести умения и навыки анализа напряженного состояния в рассматриваемой точке деформируемого тела.

Задача 1. Определение напряжений на координатных площадках

Тело движется и деформируется под действием внешних сил, распределенных на его поверхности (внешние поверхностные силы) и по объему (внешние объемные или массовые силы). В результате в нем возникают напряжения как следствие уравновешивания внешних сил. Напряжением называется величина численно равная пределу отношения силы действующей на бесконечно малую область тела к площади этой области. Напряжение является мерой интенсивности внутренних сил, распределенных по сечениям, и характеризует прочность тела в точке, так как известно, что разрушение тела начинается в точке. Различают две компоненты напряжения: 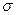- нормальное напряжение, 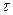- касательное. Совокупность напряжений на всех элементарных площадках, которые можно провести через какую-либо точку тела называется напряженным состоянием в данной точке.

Поскольку напряжение равно силе, отнесенной к площади, на которой она действует, единица измерения напряжения в системе СИ равна Н/м² (Па). Ввиду малости величины Н/м² на практике напряжения обычно измеряют в Н/мм² (МПа). Заметим, что 1 кгс/мм² =9,8067М7а.

Напряженное состояние точки характеризуется тензором напряжений Тs и может быть определено, если известно напряжение на любой проведенной через нее площадке. Напряженное состояние тела в свою очередь характеризуется тензорным полем

Тs= Тs (x₁,x₂,x₃, t) и слагается из напряженных состояний в каждой его точке. Если тензор напряжений одинаков во всех точках тела, то его напряженное состояние называется однородным.

Тензором называется инвариантный математический объект, задаваемый с помощью 6 чисел.

Матрица тензора напряжений в прямоугольной декартовой системе координат х, у, z имеет вид:

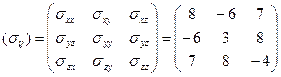(1)

Эта матрица симметрична, т. е 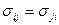или подробно: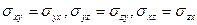

Напряжения действуют на координатных площадках х, у, z.

Первый индекс в обозначении означает координатную ось, в направлении которой действует напряжение, а второй индекс означает координатную площадку, на которой оно действует. На главной диагонали матрицы располагаются нормальные напряжения, остальные напряжения являются касательными. Из курса сопротивления материалов известен закон парности касательных напряжений 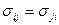Следовательно, матрица симметричная, т. е 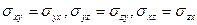. Симметрия тензора напряжений является следствием закона сохранения момента импульса.

Касательные напряжения 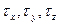, действующие на координатных площадках, находим как геометрические суммы напряжений с различными индексами i и j (см. рисунок 1):

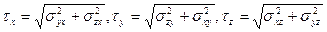(2)

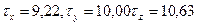
Нормальные напряжения на координатных площадках х, у, z соответственно равны:

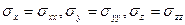
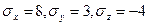
Задача 2. Графическое изображение компонент тензора напряжений

Дата добавления: 2015-06-25