Построить эллипсоид напряжений

Записать матрицу тензора напряжений в главных осях. Показать на рисунке главные нормальные напряжения с учетом их знака и величины по граням главного куба вокруг рассматриваемой точки.

Матрица тензора напряжений в главных осях имеет диагональный вид:

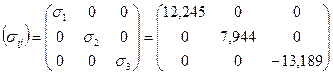(23)

Элементарный объем, представленный в форме куба, ограниченного главными площадками, называется главным кубом.

Вокруг рассматриваемой точки деформируемого тела выбираем элементарный объем в виде куба, ребра которого параллельны главным осям тензора напряжений , , . Это главный куб (рисунок 3). На его гранях и показываем главные нормальные напряжения. Положительные напряжения являются растягивающими, а отрицательные - сжимающими. На рисунке 3 напряжения и положительны, а — отрицательно.

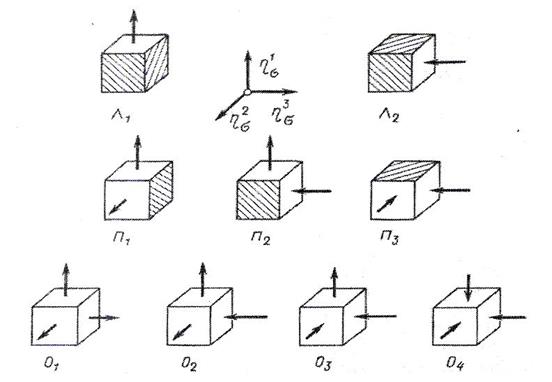
Рисунок 13 - Схемы главных нормальных напряжений

Схемы Л₁ и Л₂ соответствуют линейному напряженному состоянию; П₁ П₂, П₃ плоскому; О₁ — О₄ — объемному.

Задача 8. Построение эллипсоида напряжений

Геометрические образы напряженного состояния в точке: куб, эллипсоид, шар (если сопряженные диаметры эллипсоида равны друг другу), треугольник напряжений, звезда напряжений, диаграмма Мора.

Эллипсоид напряжений - это объемный геометрический образ напряженного состояния (см. рисунок 4). Если провести через рассматриваемую точку М деформируемого тела площадку с нормалью h, то конец вектора полного напряжения S_n на этой площадке лежит на поверхности эллипсоида. Уравнение эллипсоида напряжений:

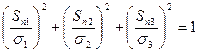
Его полуоси равны 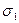, , , а поверхность является поверхностью напряжений, т. е. любая ее точка N является концом вектора напряжений S_n действующего на одной из площадок 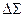, проходящей через рассматриваемую точку.

Выбираем одну из пяти аксонометрических проекций в соответствии с ГОСТ 2.317-69 «Аксонометрические проекции» с измерением №1, утвержденным в августе 1980 года:

1) прямоугольную изометрическую проекцию;

2) прямоугольную диметрическую проекцию;

3) косоугольную фронтальную изометрическую проекцию;

4) косоугольную горизонтальную изометрическую проекцию;

5) косоугольную фронтальную диметрическую проекцию.

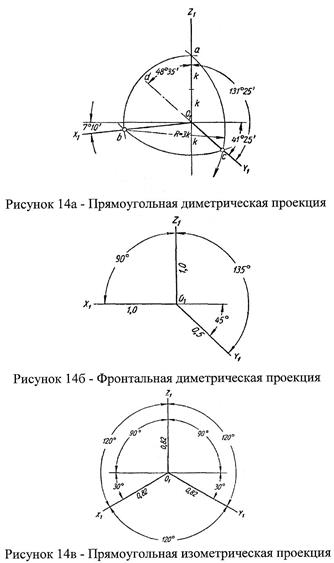
Аксонометрическая проекция — наглядное изображение, полученное методом параллельного проецирования на одну плоскость, называемую аксонометрической.

х, у, z - система пространственных осей

х', у', z' - аксонометрические оси

Коэффициент искажения (к) — называется величина отношения единичного отрезка, взятого на аксонометрической оси к его натуральной величине.

Виды аксонометрических проекций.

Классификация аксонометрических проекций ведётся по двум признакам:

1)по направлению аксонометрических лучей:

а) прямоугольные,

б) косоугольные

2) В зависимости от соотношения коэффициентов искажения по аксонометрическим осям

а) если 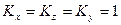- изометрия

б) если 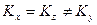— диметрия

К_у— косоугольная диметрия

в) если 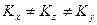- триметрия

Выбираем такую проекцию, чтобы плоское изображение эллипсоида на рисунке было наиболее наглядным.

Рассмотрим последовательность построения эллипсоида. Через точку М проводим три главные оси тензора напряжений 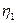, , . Они взаимно перпендикулярны, но углы между ними на рисунке зависят от выбора аксонометрической проекции.

На осях 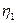, , по обе стороны от начала координат (точки М) в выбранном масштабе и с учетом коэффициентов искажения откладываем отрезки, соответственно равные 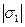, , 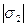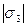. Получаем три сопряженных диаметра эллипсоида АВ, CD, EF.

Строим три эллипса, которые являются линиями пересечения поверхности эллипсоида с координатными плоскостями. В координатной плоскости 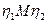эллипс строим по двум сопряженным диаметрам АВ и CD. В координатной плоскости 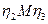эллипс строим по сопряженным диаметрам CD и EF. В координатной плоскости 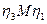эллипс строим по двум сопряженным диаметрам EF и АВ.

На рисунке 5 показано, как строить эллипс по двум сопряженным диаметрам KL и RS. Вначале строим параллелограмм, стороны которого проходят через точки К, L, R, S и параллельны диаметрам KL и RS. Диаметр RS делим на несколько равных частей. На столько же равных частей делим стороны, параллельные диаметру KL. Точки деления обозначаем, как показано на рисунке. Из точек К и L проводим через точки деления лучи. Поводим эллипс через точки К, L, R, S, а также через точки пересечения одноименных лучей.

Проводим четвертый эллипс, огибающий три уже построенные в координатных плоскостях. Он и является аксонометрической проекцией эллипсоида. В заключение выделяем видимые и невидимые линии эллипсов, расположенных в координатных плоскостях.

Задача 9. Вычисление интенсивности напряжений и угла вида напряженного состояния

Дата добавления: 2015-06-25