Показать на рисунке взаимное расположение главных осей , , и осей х, у, z

Выбираем аксонометрическую проекцию и проводим оси х, у, z (рисунок 8). Выбираем масштаб. Главную ось проводим через точку М (0, 0, 0) и через точку А с координатами (l₁, m₁, n₁). Главную ось проводим через точку с координатами (l₂, m₂, n₂). Главную ось проводим через точку М и через точку с координатами (l₃, m₃, n₃).

Замечания:

1) Если при решении задачи 12 принять n₁ < 0 и n₂ < 0, то оси и будут иметь противоположные направления. При этом ось сохранит прежнее направление. Действительно, если в формулах (37) поменять знаки всех величин, стоящих в определителях, получим те же значения и те же знаки направляющих косинусов l₃, m₃, n₃.

2) Если принять n₁ > 0, а n₂ < 0, то ось сохранит свое направление, а оси и заменят свои направления на противоположные.

3) Если принять n₁ < 0, а n₂ > 0, то ось сохранит свое направление, а оси и изменят свои направления на противоположные.

Задача 14. Нахождение острых углов между осями х, у, zи главным осями

Вычислить направляющие косинусы осей х, у, z в главной системе координат. Найти острые углы между осями х, у, z и главными осями , ,

Обозначим направляющие косинусы осей х, у, z в главной системе координат так:

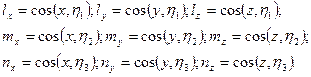
Формула для напряжений в главных осях:

,

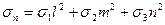а квадрат касательного напряжения равен:

.

Добавляя к формулам уравнение I² +т² +п² =1, получим систему трех уравнений, решая которую найдем квадраты направляющих косинусов.

Направляющие косинусы оси х в главной системе координат, т. е. l_x, m_x, n_х найдем по формулам:

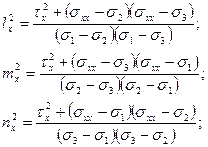(40)

Обратим внимание на то, что формулы (40) получается одна из другой круговой заменой индексов 1, 2, 3. Извлекая квадратные корни, берем положительные значения l_x, m_x, n_х.

Направляющие косинусы оси у в главной системе координат, т. е. l_y, m_y, n_у найдем по темже формулам (40), заменив в них предварительно все индексы х на индексы у:

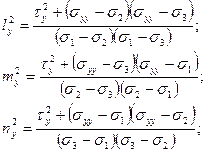
Направляющие косинусы оси z в главной системе координат, т. е. l_z, m_z, n_z найдем по формулам (40), заменив в них все индексы х на индексы z:

Вычисленные направляющие косинусы (39) записываем в столбец 3 табл. 2. Если вычисления сделаны правильно, то с точностью до знака они совпадают с направляющими косинусами в столбце 1.

Острые углы между осями х, у, z и главными осями , , обозначим и вычислим так:

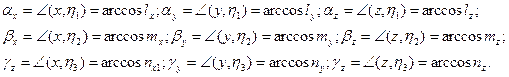(41)

Углы , , 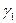это углы между осью и осями X, Y, Z, а 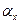, , 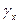углы между осью х и осями , , . Если углы , , 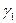больше , то они равны углам , , .

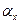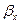Значения этих углов записываем в столбец 4 табл. 2. Если вычисления сделаны правильно, то эти углы:

1) совпадают с углами в столбце 2, если углы в столбце 2 меньше 90°, т. е. также являются острыми;

2) являются дополнениями углов в столбце 2 до 180°, если углы в столбце 2 больше 90°, т.е. являются тупыми.

Острые углы между осями х, у, z и главными осями , , :

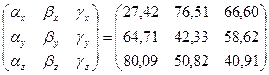
Задача 15. Проверочные расчеты

Проверить правильность вычисления главных нормальных напряжений 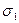, , 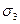в задаче 6 и направляющих косинусов в задаче 14. С этой целью, рассматривая площадки х, у, z, как наклонные к главным осям , , , найти нормальные , , и касательные , , 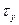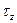. напряжения на этих площадках.

Напряжения на площадках, наклоненных к главным осям.

Нормальные напряжения: .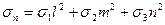

Квадрат касательных напряжений равен:

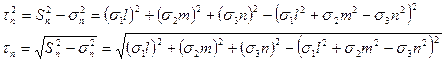
Из приведенных выражений круговой заменой индекса можно получить формулы для нахождения напряжений на площадках, наклонных к главным осям.

Одинаковые по величине напряжения действуют на восьми октаэдрических площадках, проходящих через рассматриваемую точку тела.

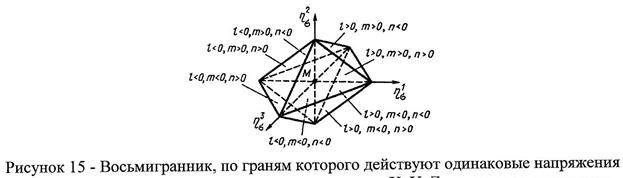
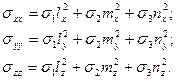(42)

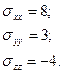
Полученные значения совпадают с заданными.

Касательные напряжения на координатных площадках х, у, z соответственно равны:

(43)

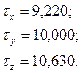
Полученные значения совпадают со значениями касательных напряжений полученными по формулам (2) в задаче 1.

Задача 16. Построение диаграммы Мора. Графическое решение задач.

С помощью диаграммы Мора графически проверить правильность вычисления в задаче 14 углов между осями х, у, z и главными осями , ,

На диаграмме Мора точка А, принадлежащая криволинейному треугольнику, образованному тремя главными окружностями, соответствует площадкам, на которых напряжения равны 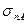и

Точки на диаграмме Мора, расположенные на главных окружностях I, II. III, соответствуют площадкам действия главных касательных напряжений.

Вначале найдем графически острые углы 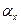, , 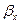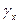между осью х и главными осями , , смотри формулы (41).

Имея главные нормальные напряжения 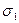, , 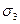и выбрав масштаб, строим диаграмму Мора для напряжений (рисунок 9). Отмечаем на ней точку А_х, соответствующую площадке х, по ее координатам: на площадке х нормальное напряжение равно 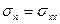, а касательное напряжение равно .

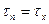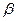Через точку А_х проводим три дуги окружностей = const, = const, 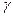= const с центрами соответственно в точках O₁ ,O₂,О₃, являющимися центрами главных кругов Мора I, II, III. Точки пересечения этих окружностей с главными окружностями I, II, III соединяем радиусами с центрами O₁ ,O₂,О₃.

Около центров O₁ ,O₂,О₃ с помощью транспортира измеряем углы 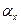2 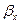, 2 , 2 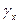по или против часовой стрелки, как показано на рисунке 9. Найденные с помощью диаграммы Мора углы 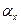, , 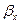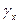записываем в столбец 5 таблицы 2. Они должны совпадать с одноименными углами, найденными расчетом (смотри столбец 4 таблица 2).

Острые углы , , 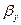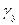между осью у и главными осями , , найдем, построив второй раз диаграмму Мора и отметив на ней точку А_у, соответствующую площадке у, по ее координатам , .

Углы 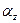, , 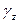между осью z и главными осями , , найдем, построив в третий раз диаграмму Мора и отметив на ней точку A_z, соответствующую площадке z, по ее координатам , .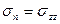

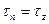Величина 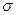не влияет на геометрическое построение диаграммы Мора и треугольника напряжений. При изменении 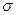меняется координата точки М в звезде напряжений.

Среднее напряжение 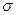влияет на величину угла виды напряженного состояния и невлияет на интенсивность напряжений, а так же на главные нормальные напряжения.

Список используемой литературы:

1. Кучеряев Б. В. Механика сплошных сред: Учебник для вузов. М.: МИСиС, 1999.-320с.

2. Александров А. В., Потапов В. Д. Основы теории упругости и пластичности: Учебник для вузов. - М.: Высш. шк., 1990.-398с.

3. Зубчанинов В. Г. Основы теории упругости и пластичности: Учебник для вузов. — М.: Высш. шк., 1990.

4. Колмогоров В. Л. Механика обработки металлов давлением: Учебник для вузов. -М.: Металлургия, 1986. - 456с.

5. Аркулис Г. Э., Дорогобид В. Г. Теория пластичности: Учеб. пособие для вузов. -М.: Металлургия, 1987. — 352с.

Таблица 2

Величины, характеризующие взаимное расположение главных осей

Тензора напряжений , , и осей x, y, z

Направляющие косинусы главных осей η1, η2, η3 относительно осей x, y, z	Углы между главными осями η1, η2, η3 и осями x, y, z	Направляющие косинусы осей x, y, z относительно главных осей η1, η2, η3	Острые углы между осями η1, η2, η3, полученные
расчетом	графически
0,8876	27,42	0,8877	27,42	30,5
-0,4271	115,29	0,4271	64,71	65,5
0,1722	80,08	0,1721	80,09	78,5
0,2331	76,52	0,2332	76,51	80,6
0,7393	42,33	0,7392	42,33	45,5
0,6318	50,82	0,6318	50,82	52,5
-0,3971	113,40	0,3971	66,60	68,5
-0,5207	121,38	0,5207	58,62	57,25
0,7558	40,90	0,7558	40,91	38,9

Дата добавления: 2015-06-25