Построить звезду напряжений. Графически найти главные нормальные и главные касательные напряжения, сравнить с результатами расчета главных напряжений в задаче 6

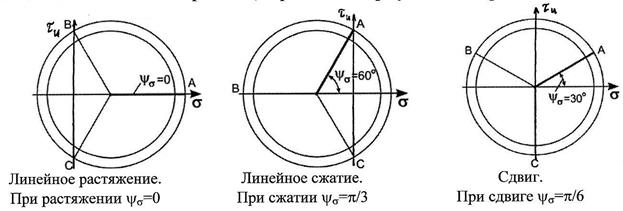
Звезду напряжений строим в координатах 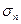(нормальное напряжение), 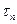(касательное напряжение) (рисунок 7). Центр звезды - точка М находится на оси 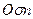. Координата центра звезды равна среднему напряжению 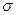(формула 29).Проводим две окружности, с центром в точке М. Радиус большей окружности равен 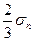. Радиус меньшей окружности равен интенсивности касательных напряжений 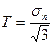. Из точки М проводим три луча, образующие собственно звезду, углы между которыми равны 120°. Угол между первым лучом МА и осью 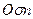равен углу вид напряженного состояния .

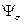Луч ОА составляет с осью 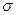угол 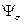, тогда абсциссы точек А, В, С равны главным нормальным напряжениям. Т. е. длина проекции отрезка ОА' на ось 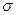будет равна:

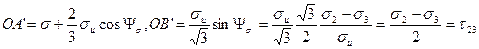
С учетом выбранного масштаба, абсциссы точек пересечения лучей с большой окружностью равны главным нормальным напряжениям 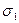, , 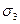. Ординаты точек пересечения лучей с малой окружностью равны главным касательным напряжениям , ,

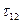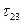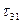
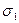=12,245; =7,944; 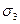=-13,189;

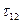=2,150; 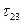=10,567; 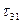=-12,717.

Полученные данные хорошо согласуются с результатами расчетов в задаче 6.

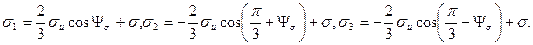
Задача 12. Определение положения главных осей тензора напряжений

Найти направляющие косинусы главных осей тензора напряжений в старой системе координат. Найти углы между главными осями и осями х, у, г.

Аналитически углы между главными осями тензора напряжений и осями X, Y, Z можно найти по формулам:

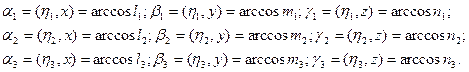
Направляющие косинусы главных осей тензора напряжений 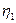, , в старой системе

координат х, у, z обозначим так:

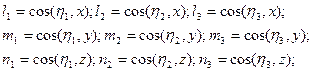(31)

Эти направляющие косинусы найдем, решая три системы уравнений. Положениеглавной оси 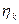будем характеризовать направленным по ней единичным вектором 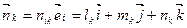, компоненты которого 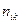в произвольной системе координат

найдем, решая систему уравнений 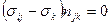. Например, направляющие косинусы l₁, m₁, n₁ главной оси найдем, решая систему уравнений:

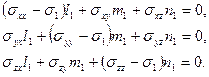(32)

при условии

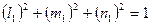(33)

Формулы Крамера для решения системы линейных алгебраических уравнений:

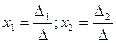ит.д.,

где 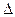- определитель матрицы,

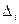- определитель, полученный из 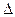заменой i-гo столбца, столбцом свободных членов.

Система уравнений (32) однородная (справа стоят нули) поэтому решить её по формулам Крамера нельзя, поскольку в числителях будут нули. Поэтому определитель

системы (32) равен нулю, тогда имеем неопределенность .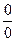

Последовательность решения системы уравнений следующая. Из первых двух уравнений (32) выражаем l₁ и m₁ через n₁, например, по формулам Крамера:

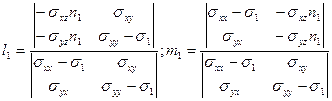(34)

Полученные выражения l₁ и m₁ через n₁ подставляем в выражение (33). Получаем квадратное уравнение относительно n₁. Решая его, находим n₁. При этом принимаем n₁>0. Затем находим l₁ и m₁. Случай, если принять n₁ < 0, рассмотрен в задаче 13.

Аналогично находим направляющие косинусы 1₂, m₂, m₂ главной оси .

Направляющие косинусы l₁, m₁, n₁ главной оси находим из условия, что направляющий вектор 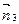главной оси есть векторное произведение направляющих векторов 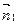и 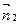главных осей и , т. е.

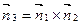, (35)

так как главные оси , , образуют правую прямоугольную декартову систему координат.

Запишем формулу (35) через направляющие косинусы главных осей:

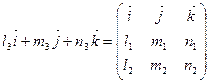. (36)

Разложением определителя по первой строке, получим:

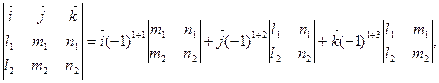
откуда и найдем, что

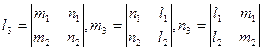(37)

Уравнения направляющих векторов главных осей тензора напряжений в системе координат х, y, z:

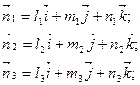
Результаты расчета направляющих косинусов (31) записываем в столбце 1 табл. 2.

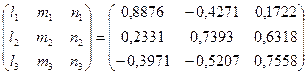
Углы между главными осями , , и осями х, у, z обозначим и вычислим так:

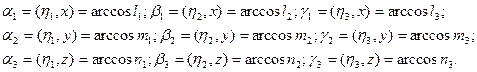
При этом нужно иметь в виду, что arccos(-х) = 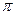- arccos x. Найденные значения углов между главными осями и осями х, у, z записываем в столбец 2 таблицы 2.

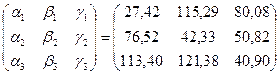
Задача 13. Построение главных осей тензора напряжений

Дата добавления: 2015-06-25