
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задать три угла Эйлера. Вычислить направляющие косинусы новых осей в старой системе координат
|
|
|
|
Старые оси координат обозначены х, у, z. Новые оси обозначим х', у', z'. Положение новых осей относительно старых однозначно определяется тремя углами Эйлера 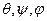 (рисунок 2).
(рисунок 2).
Угол нутации 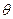 - между положительными направлениями осей Oz' и Oz (
- между положительными направлениями осей Oz' и Oz (  >
>  0),
0), 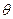 =60°.
=60°.
Угол процессии  - между осью Ох и линией пересечения ОА плоскостей хОу и х'Оу'. На линии ОА выбрано положительное направление так, что ОА, Oz, Oz' образуют правую тройку векторов. Угол
- между осью Ох и линией пересечения ОА плоскостей хОу и х'Оу'. На линии ОА выбрано положительное направление так, что ОА, Oz, Oz' образуют правую тройку векторов. Угол  отсчитывается в направлении от Ох к Оу (
отсчитывается в направлении от Ох к Оу ( ),
),  =150°.
=150°.
Угол чистого вращения 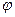 - между Ох' и ОА; угол
- между Ох' и ОА; угол 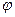 отсчитывается в направлении от Ох' и Оу' (
отсчитывается в направлении от Ох' и Оу' ( ),
), 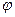 =315°.
=315°.
Обозначим
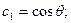

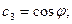

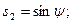
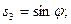 (6)
(6)
Обозначим далее направляющие косинусы новых осей в старой системе координат так:
l’1=cos(x’,x); m’1=cos(x’,y); n’1=cos(x’,z);
l’2=cos(y’,x); m’2=cos(y’,y); n’2=cos(y’,z);
l’3=cos(z’,x); m’3=cos(z’,y); n’3=cos(z’,z). (7)
Тогда эти направляющие косинусы равны
l’1= c2c3-c1s2s3; m’1= s2c3-c1c2s3); n’1=s1s3;
l’2= -c2s3-c1s2c3; m’2= -s2s3-c1c2c3; n’2=s1c3;
l’3=s1s2; m’3=-s1c2; n’3=c1. (8)
Направляющие косинусы новых осей в старой системе координат (ось z' совпадает с осью z, а оси х', у' повернуты относительно старых осей х, у на угол  ):
):
l’1=cos( ); m’1=cos(
); m’1=cos(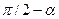 ); n’1=cos(
); n’1=cos( );
);
l’2=cos(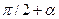 ); m’2=cos(
); m’2=cos( ); n’2=cos(
); n’2=cos( );
);
l’3=cos( ); m’3=cos(
); m’3=cos( ); n’3=1;
); n’3=1;

Задача 5. Преобразование компонент тензора напряжений к новой системе координат
Найти компоненты тензора напряжений в новой системе координат. Убедиться в правильности расчетов, вычислив инварианты тензора напряжений через его компоненты в новой системе координат.
Компоненты тензора напряжений в старой системе координат х, у, z обозначены  (
(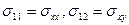 и так далее).
и так далее).
Компоненты тензора напряжения в новой системе координат х', у', z' обозначим 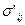 (
( и так далее). Они выражаются через компоненты тензора напряжений в старой системе координат так
и так далее). Они выражаются через компоненты тензора напряжений в старой системе координат так
 ,
,
где по индексам р и q производится суммирование от 1 до 3. (9)
В подробной записи имеем девять формул, так как свободных индексов два — i и j.
Элементы матрицы преобразования В=(bij) равны частным производным новых координат по старым:
 (10)
(10)
При жестком повороте осей координат новые координаты выражаются через старые так:
x’=l’1x+m’1y+n’1z;
y’=l’2x+m’2y+n’2z; (11)
z’=l’3x+m’3y+n’3z.
Тогда элементы матрицы преобразования В равны:
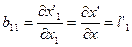 ;
; 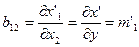 ;
;  ;
;
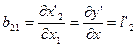 ;
;  ;
; 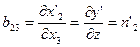 ;
;
 ;
; 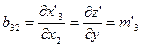 ;
; 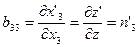 .
.
Итак, элементы матрицы преобразования В равны направляющим косинусам новых осей х', у', z' относительно старых осей х, у, z:
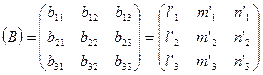 (12)
(12)

Тогда, например, по формуле (9) найдем:
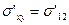 =
= 
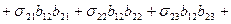
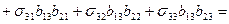
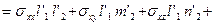
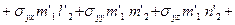
 .
.
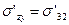 =
= 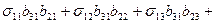




 .
.
Формулу (7) можно записать в матричной, безиндексной форме:
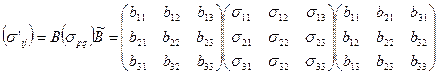 , (14)
, (14)
где 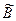 - транспонированная матрица. Матрицу
- транспонированная матрица. Матрицу 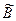 получим, поменяв местами строки и столбцы в матрице В.
получим, поменяв местами строки и столбцы в матрице В.
 .
.
Инварианты тензора напряжений I’1, I’2, I’3 через его компоненты в новой системе координат вычислим по формулам (3) – (5) для I’1, I’2, I’3, заменив в них  на
на 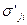 .
.
I’1=7,
I’2=-169,
I’3=-1283.
Вычисления по формулам (9) выполнены верно, т.к I1=I’1, I2=I’2, I3=I’3.
Задача 6. Вычисление главных нормальных и главных касательных напряжений.
Вычислить главные нормальные и главные касательные напряжения. Убедиться в правильности расчетов, вычислив инварианты тензора напряжений через главные нормальные напряжения.
Напряжения действующие на три взаимно перпендикулярные главные площадки, перпендикулярные главным осям тензора напряжений, называют главными нормальными напряжениями.
В точке М всегда можно выбрать такую прямоугольную декартову систем координат 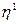 ,
, 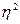 ,
,  , в которой уравнение тензорной поверхности Tijdxidxj=Tijdx’idx’j =С примет канонический вид
, в которой уравнение тензорной поверхности Tijdxidxj=Tijdx’idx’j =С примет канонический вид  . Такая прямоугольная декартова система координат называется главной системой координат тензора Т в точке М. Оси
. Такая прямоугольная декартова система координат называется главной системой координат тензора Т в точке М. Оси 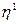 ,
, 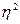 ,
, 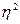 называются главными осями тензора. Единая для всего деформируемого тела главная система координат может быть введена, если тело однородное, и на всех его точках действуют одинаковые напряжения.
называются главными осями тензора. Единая для всего деформируемого тела главная система координат может быть введена, если тело однородное, и на всех его точках действуют одинаковые напряжения.
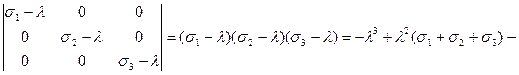

Главные нормальные напряжения  ,
, 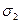 ,
,  равны корням кубического уравнения
равны корням кубического уравнения
 (15)
(15)
Кубическое уравнение решим методом тригонометрических подстановок. В начале приведем его к каноническому виду, когда коэффициент при квадрате неизвестного равен нулю. С этой целью заменим:
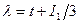 , (16)
, (16)
где t - новая переменная.
Получим:
 (17)
(17)
Раскроем скобки и сформируем коэффициенты при t3 (он равен единице), при t2 (он равен нулю), при t (обозначим его Зр), а также свободный член (обозначим его 2q). Итак, получим кубическое уравнение
t3+3pt+2q=0 (18)
р = -61,7778
q = 431,6269
Вычислим 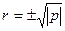 . Знак r должен совпадать со знаком q
. Знак r должен совпадать со знаком q
r = 485,5662
Вычислим далее вспомогательную величину
cos 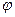 = q / r3 (19)
= q / r3 (19)
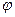 =2,6658
=2,6658
Тогда корни кубического уравнения равны:
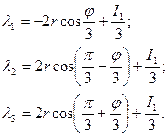 (20)
(20)
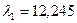 ;
;
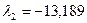 ;
;
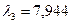 .
.
Так как  , то
, то 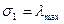 , а
, а  . Здесь
. Здесь  — максимальный, а
— максимальный, а 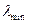 — минимальный корни кубического уравнения.
— минимальный корни кубического уравнения.
 ;
;
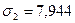 ;
;
 .
.
Главные касательные напряжения равны полуразностям главных нормальных напряжений, и действуют на площадках, параллельных главным осям и равнонаклоненных к ним:
 , (21)
, (21)
где 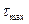 — максимальное главное касательное напряжение.
— максимальное главное касательное напряжение.

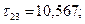
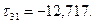

Инварианты тензора напряжений через главные нормальные напряжения вычислим по формулам:

 (22)
(22)
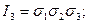
Если они совпадают с инвариантами, найденными в задаче 3 по формулам (3)-(5), главные нормальные напряжения вычислены правильно.
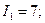
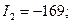
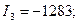
Задача 7. Построение главного куба напряжений
|
|
|
|
|
Дата добавления: 2015-06-25; Просмотров: 1651; Нарушение авторских прав?; Мы поможем в написании вашей работы!