Средства композиции

Пропорции. В математике пропорцией (от лат. ргорогПо) называется равен­ств между двумя отношениями четырех величин а: Ь = с: с1, в искусстве — *р:<порции — размерные соотношения элементов формы.

С древнейших времен человечество было занято поиском формулы красоты. Наминая с древнегреческих философов, математиков и художников проводи­лись теоретические исследования для нахождения самых совершенных гармо­ничных пропорций. Гармония (от греч. Ьагтота — связь, стройность, соразмер­ность) — соразмерность частей, слияние различных компонентов объекта в слнное органичное целое. В древнегреческой философии гармония рассматри­валась как организованность космоса, противостоящая хаосу, в истории эсте­тки — как существенная характеристика прекрасного.

Известный древнегреческий мыслитель и математик Пифагор Самосский (VI в. до м > I изучал свойства целых чисел и пропорций. Он хотел «алгеброй проверить гармо-ним«. Пифагор и его последователи считали число как основу всего существующего, а числовые отношения — источником гармонии космоса. Они утверждали, что треуголь­ник есть первоисточник рождения и сотворения различных видов вещей. Отсюда дошла до наших дней теорема Пифагора с его знаменитым треугольником: прямоугольный грсиольник с углами в 30, 60 и 90° и гармоничным соотношением его сторон. Кроме того. Пифагор считал, что квадрат в большей степени, чем любая другая фигура, нгсет в себе образ «божественной природы». Это была излюбленная им математическая фигура, которая символизировала высокое достоинство, так как прямизна углов пере-хаст целостность, а качество сторон способно устоять перед силой. Видимо, те же качества подразумевалась и в «Черном квадрате» К.Малевича.

Пропорции можно разделить на две группы: простые (основанные на рациональ­ных числах) и сложные (основанные на иррациональных числах, производных геомет­рических построений). Простые пропорциональные отношения выражаются простыми числами. К ним относится так называемый египетский треугольник с гармоничным соотношением сторон 3:4:5 (рис. 3.3, а).

Архитектор эпохи Возрождения Л.Б.Альберти в своем сочинении «Десять книг о зодчестве» писал: «Вновь и вновь следует повторить изречение Пифагора: «Нет сомне­ний, что природа во всем остается себе подобной. Дело обстоит так: существуют числа, благодаря которым гармония звуков пленяет слух, эти же числа преисполняют и гла­за, и дух чудесным наслаждением». Музыкальная аналогия навела Альберти на мысль о том, что глазу доставляет наслаждение наблюдать пропорции, представляемые в виде отношений целых чисел. Например, числа 1, 3, 5, 7, 9, 11... образуют арифметическую прогрессию, а последовательность чисел 1, 1/2, 1/3, 1/4... — гармоническую последо­вательность. Он использовал музыкальные пропорции для того, чтобы установить вза­имосвязь между тремя измерениями: высотой, длиной и шириной.

Древние греки вывели иррациональное число Ф(ф), которое символизиро­вало пропорции «золотого сечения». Буква Ф — первая греческая буква в имени великого скульптора Фидия, который часто использовал пропорции «золото­го сечения» в своих скульптурах. Термин «золотое сечение» появился намного позднее. Таким образом, число Ф как раз и равнялось отношению отрезков при делении прямой в «крайнем и среднем» положениях: АВ:ВЕ = АЕ:АВ = Ф (рис. 3.3, б).

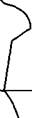
а б

Рис. 3.3. Пропорциональные отношения: а — в египетском треугольнике; б — пропорции «золотого сечения»

Много замечательных свойств числа Ф было описано в трактате итальянского мате­матика XV в. Л. Пачоли, который изложил теорию геометрических пропорций с иллю­страциями Леонардо да Винчи. Он исследовал «золотой прямоугольник», который об-

Глава 5 ОСНОВЫ ПРОЕКТИРОВАНИЯ ОДЕЖДЫ

Проектирование одежды — процесс создания нового образца одежды с за­данными свойствами, включающий исследование, создание эскизов, макетов и моделей, расчеты и построение чертежей изделий, изготовление опытных образцов. На основе проведенных предпроектных исследований и анализа ана­логов рождается творческая концепция, которая воплощается прежде всего в образе. Образ рождается либо на бумаге при создании эскиза и затем воплоща­ется в макет, затем в модель, либо при работе непосредственно с материалом в процессе макетирования, и макет воплощается в модель.

Дата добавления: 2015-06-25