Момент силы относительно центра (или точки)

Момент силы относительно центра. Пара сил

Введем важное понятие о моменте силы относительно точки. Точку, относительно которой берется момент, называют центром момента, а момент силы относительно этой точки – моментом относительно центра.

Если под действием приложенной силы тело может вращаться вокруг некоторой закрепленной точки, то момент силы относительно этой точки будет характеризовать вращательный эффект силы. Вращательное действие силы на тело будет зависеть от модуля силы, расстояния линии действия силы до точки закрепления и от направления вращения в этой плоскости.

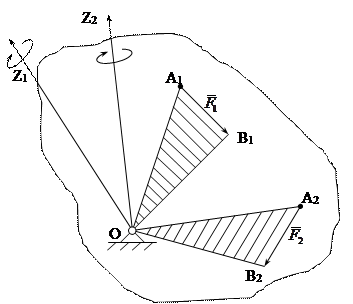
Рисунок 5.1

Так, например, если к телу, закрепленному неподвижно в точке О (рисунок 5.1), приложена в точке A₁ сила 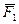, то тело будет вращаться вокруг оси OZ₁, перпендикулярно плоскости треугольника OA₁B₁, в направлении, указанном на рисунке. Если к этому же телу приложена сила в точке A₂, то тело будет вращаться вокруг оси OZ₂, перпендикулярно к плоскости треугольника OA₂B₂.

Мерой вращательного действия силы на тело с закрепленной точкой является момент силы относительно точки.

Алгебраическая величина момента силы относительно точки, определяется произведением модуля силы на ее плечо.

Рассмотрим силу F, приложенную в точке А (рисунок 5.3). Из некоторого центра О опустим перпендикуляр на линию действия силы ; длину h этого перпендикуляра называют плечом силы относительно центра О.

Рисунок 5.2

Момент силы относительно центра О определяется:

1) модулем момента, равным произведению F·h;

2) положением в пространстве плоскости ОАВ («плоскости поворота»), проходящей через центр О и силу ;

3) направлением поворота в этой плоскости.

Из геометрии известно, что положение плоскости в пространстве определяется направлением нормали «n» (перпендикуляра) к этой плоскости. Таким образом, момент силы относительно центра характеризуется не только его числовым значением, но и направлением в пространстве, т.е. является величиной векторной.

Моментом силы F относительно центра О называется приложенный в центре О вектор , модуль которого равен произведению модуля силы на ее плечо h и который направлен перпендикулярно плоскости, проходящей через центр О и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки (рисунок 5.3).

Согласно этому определению

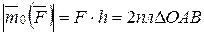(5.1)

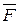Этот результат следует из того, что пл. Δ ОАВ= АВ·h/2=Fh/2. Измеряется момент силы в Ньютон-метрах (Нм). Выведем формулу, для вектора-момента силы относительно точки О. Для этого рассмотрим векторное произведение векторов и (рисунок 5.3). Как известно из векторной алгебры, это будет вектор, перпендикулярный к плоскости, в которой расположены векторы и 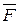, и направленный в такую сторону, чтобы с его конца видеть поворот от к 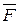кратчайшим путем против хода часовой стрелки. Модуль этого вектора или .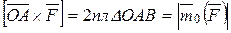

Поэтому

или , (5.2)

где – радиус-вектор точки А, проведенный из центра О.

Таким образом, вектор-момент силы относительно точки равен векторному произведению радиуса-вектора точки приложения силы на вектор силы.

Обозначая алгебраическое значение момента силы относительно точки О через 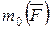, будет иметь

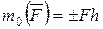(5.3)

Из формулы (5.3) следует, момент силы относительно точки, лежащей на линии действия этой силы, равен нулю (т.к. h=0).

Пример.

Вычислить моменты сил , относительно точки O.

Решение

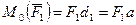
Вектор направлен перпендикулярно плоскости OAEN, т.е. по прямой OL. 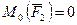, т.к. линия действия силы проходит через точку O.

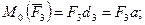
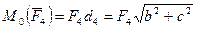
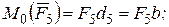
Векторы и 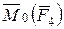перпендикулярны к плоскости ОВDN, но направлены в противоположные стороны. Вектор 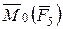перпендикулярен к плоскости ОАВL и направлен по прямой ON.

5.2 Пара сил. Момент пары сил

Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело (рисунок 5.3, а).

а) б)

Рисунок 5.3

Система сил 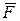, , 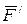образующих пару, не находится в равновесии (эти силы не направлены вдоль одной прямой). В то же время пара сил не имеет равнодействующей, т.к. равнодействующая любой системы сил равна ее главному вектору 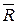, т.е. сумме этих сил, но для пары сил , поэтому свойства пары сил, как особой меры механического взаимодействия тел, рассмотрим отдельно.

Плоскость, проходящая через линии действия пары сил называется плоскостью действия пары. Расстояние d между линиями действия сил пары называется плечом пары. Действие пары сил на твердое тело сводится к вращательному эффекту, который характеризуется величиной, называемой моментом пары. Этот момент определяется:

1) Его модулем, равным произведению F·d;

2) положением в пространстве плоскости действия пары;

3) направлением поворота пары в этой плоскости.

Таким образом, как и момент силы относительно центра, это величина векторная. Поэтому моментом пары сил называется вектор (или ), модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки (рисунок 5.3, б).

Следует отметить, что так как плечо силы 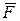относительно точки А равно d (рисунок 5.3, а), а плоскость, проходящая через точку А и силу 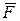, совпадает с плоскостью действия пары, то одновременно .

В отличие от момента силы 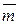может быть приложен в любой точке (такой вектор называется свободным). Измеряется момент пары, как и момент силы, в Н·м.

Покажем, что моменту пары можно дать другое выражение: момент пары равен сумме моментов относительно любого центра О сил, образующих пару, т.е.

(5.4)

Для доказательства проведем из произвольной точки О (рисунок 5.4) радиусы-векторы 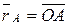и .

Рисунок 5.4

Тогда согласно формуле (5.2), учитывая, что , получим ;

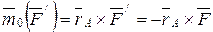и, следовательно,

Так как , то справедливость (5.4) доказана. Отсюда следует, что 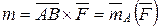или (5.5)

т.е. момент пары равен моменту одной из ее сил относительно точки приложения другой силы. Отметим еще, что модуль момента пары

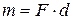(5.5^/)

Так как действие пары сил на твердое тело определяется значением суммы моментов сил пары относительно любого центра О, то из формулы (5.4) следует, что две пары сил, имеющие одинаковые моменты, эквивалентны, т.е. оказывают на тело одинаковое механическое действие. Это означает, что две пары сил, независимо от того, где каждая из них расположена в данной плоскости (или в параллельных плоскостях) и чему равны в отдельности модули их сил и их плечи, если моменты имеют одно и то же значение 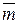, будут эквивалентны. Так как выбор центра О произволен, то вектор 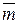можно считать приложенным в любой точке, т.е. это свободный вектор.

В дальнейшем будем на чертеже вместо пары изображать полностью ее характеризующий вектор 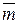. При этом модуль 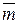определяет модуль момента пары [формула (5.5)], а направление 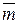определяет плоскость действия пары и направление поворота в этой плоскости.

Из формулы (5.4) следует, еще, что если на тело действует несколько пар с моментами ; 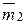…. , то сумма моментов всех сил, образующих эти пары относительно любого центра будет равна + +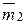…+ , а следовательно, вся совокупность этих пар эквивалентна одной паре с моментом

(5.6)

Этот результат выражает теорему о сложении пар.

Из формулы (5.6) следует, при равновесии системы пар, действующих на твердое тело, должно быть

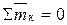или (5.7)

Таким образом, отметим следующие свойства пар сил:

1) Пары сил, лежащие в одной плоскости, эквивалентны, если их моменты численно равны и одинаковы по знаку.

2) Пару сил, не изменяя ее действия на твердое тело, можно переносить в любое место в плоскости ее действия, поворачивать ее плечо на любой угол, а также изменять величины ее момента и направления вращения.

3) Пары сил в пространстве эквивалентны, если их моменты геометрически равны.

4) Не изменяя действия пары сил на твердое тело, пару сил можно переносить в любую плоскость, параллельную плоскости ее действия, а также изменять ее силы и плечо, сохраняя неизменным модуль и направление ее момента. Таким образом, вектор-момент пары можно переносить в любую точку, т.е. вектор-момент пары сил является свободным вектором.

5) Геометрическая сумма моментов составляющих пар равна моменту эквивалентной им пары сил:

или

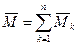(5.7)

6) Пары сил, произвольно расположенные в пространстве, взаимно уравновешиваются в том случае, если геометрическая сумма их моментов равна нулю, т.е. условие равновесия пар сил в пространстве имеет вид:

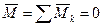(5.8)

7) Момент пары сил эквивалентной системе пар сил на плоскости, равен алгебраической сумме моментов составляющих пар:

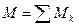(5.9)

8) Пары сил, расположенные в одной плоскости, взаимно уравновешиваются, если алгебраическая сумма их моментов равна нулю.

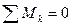(5.10)

Т.е. выражение 5.10 является условием равновесия пар сил на плоскости, а (5.8) – в пространстве.

Вопросы для самоконтроля

Момент силы относительно точки

1. Что называется моментом силы относительно точки?

2. Как направлен вектор момента силы относительно точки?

3. Запишите формулу, по которой определяется алгебраический момент силы относительно точки.

4. Какой площадью можно определить числовое значение момента силы относительно заданной точки?

5. Изменится ли момент силы относительно данной точки при переносе силы вдоль линии ее действия?

6. В каком случае момент силы относительно данной точки равен нулю?

7. Определите геометрическое место точек пространства, относительно которых моменты данной силы:

a. геометрически равны;

b. равны по модулю.

8. Определите момент силы относительно точки O, если F=200H; OA=0.5м (рисунок 6,а).

Рисунок 6

9. Определить моменты сил 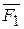и 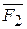относительно координатных осей, если 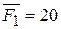КН, 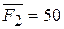КН, ОА = 0,4 м; ОВ = 0,6 м; ОС = 0,3 м (рисунок 6,б).

Пара сил

1. Какая система сил называется парой?

2. Почему пара сил не имеет равнодействующей?

3. Чем характеризуется действие пары сил на тело?

4. Как направлен вектор момента пары сил?

5. Как определяются моменты пар сил, лежащих в одной плоскости.

6. Каковы условия эквивалентности пар сил на плоскости и в пространстве?

7. Какие преобразования пары не изменяют ее действие на твердое тело?

8. Почему момент пары сил является свободным вектором?

9. ему равен момент сил, эквивалентной двум парам сил, расположенным в перпендикулярных плоскостях, если M₁=10мм; М₂=20нм?

10. Чему равен момент пары сил, эквивалентной системе пар сил, расположенных в пространстве и в одной плоскости?

11. Каковы условия равновесия системы пар сил, расположенных в пространстве и в одной плоскости?

12. Чем можно уравновесить заданную пару сил?

Дата добавления: 2015-06-04