
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. Данный закон распределения является непрерывным
|
|
|
|
Данный закон распределения является непрерывным.
1) По свойству плотности (дифференциальной функции):
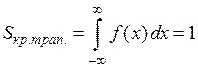
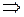
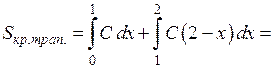
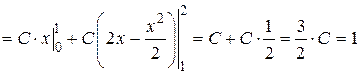
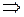
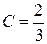 .
.
Получаем функцию:
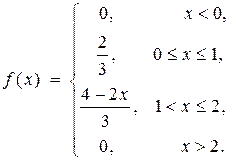
| и ее график (рис. 3). | 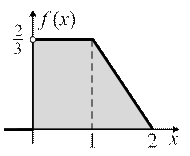
|
| Рис. 3 |
2) Найдём интегральную функцию, учитывая свойства:
· если 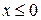 , то
, то 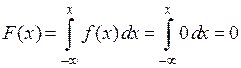 ;
;
· если 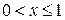 , то
, то
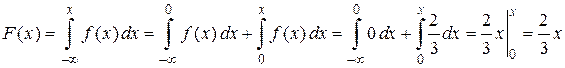 ;
;
· если 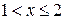 , то
, то
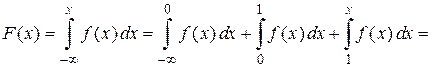
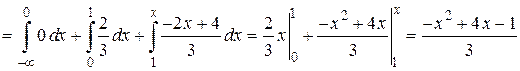 .
.
· если 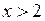 , то
, то
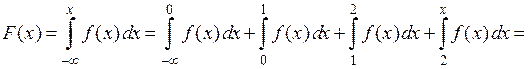
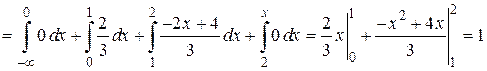 .
.
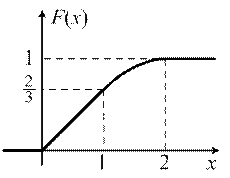
В итоге получаем функцию и её график (рис. 4)
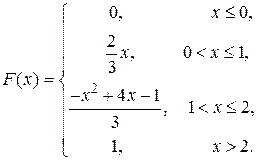
| 
|
| Рис. 4 |
3) Вычислим числовые характеристики:
· математическое ожидание:
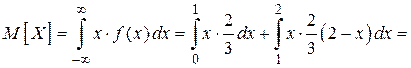
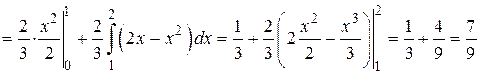 ;
;
· дисперсию по формуле 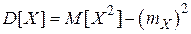 :
:
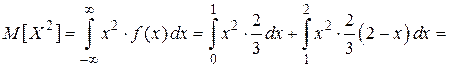
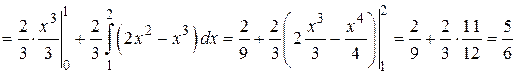 ;
;
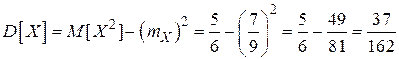 ;
;
· среднее квадратическое отклонение: 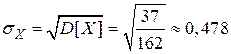 .
.
4) Найдём вероятность того, что СВ X примет значения из интервала 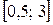 двумя способами:
двумя способами:
q 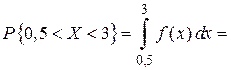
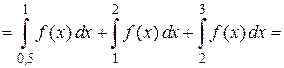
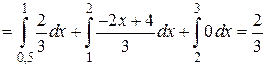 .
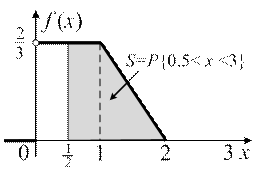
Здесь вероятность численно равна площади выделенной фигуры (рис. 5).
q .
Здесь вероятность численно равна площади выделенной фигуры (рис. 5).
q 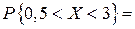
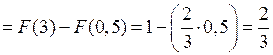 .
В этом случае вероятность численно равна длине отрезка на оси .
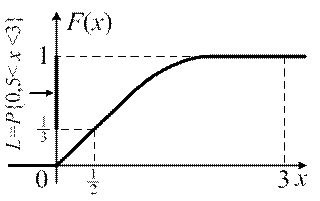
В этом случае вероятность численно равна длине отрезка на оси 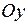 (рис. 6).
При этом результаты вычислений совпадают при различных способах. (рис. 6).
При этом результаты вычислений совпадают при различных способах.
| 
|
| Рис. 5 | |
| |
| Рис. 6 |
Ответ: 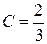 ;
; 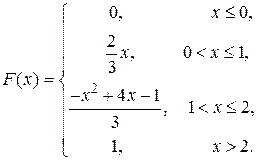
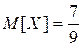 ;
; 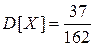 ;
; 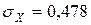 ;
; 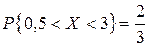 .
.
Задание № 14. В результате опыта получена выборочная совокупность:
1. По данной таблице составить интервальный вариационный ряд, разбив всю вариацию на 8-10 интервалов.
2. По сгруппированным данным построить:
| а) | полигон относительных частот; |
| б) | гистограмму относительных частот; |
| в) | график эмпирической функции распределения. |
3. Найти числовые характеристики выборочной совокупности: 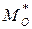 ,
, 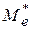 ,
, 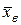 ,
, 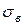 , s.
, s.
4. Построить:
| а) | на чертеже гистограммы её теоретический аналог 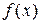 ; ;
|
| б) | на чертеже эмпирической функции 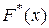 её теоретический аналог её теоретический аналог 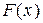 . .
|
5. По виду гистограммы и эмпирической функции распределения выборки выдвинуть гипотезу о распределении генеральной совокупности.
6. Проверить выполнение правила «трёх сигм».
7. Применив критерий согласия Пирсона 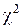 с заданным уровнем значимости
с заданным уровнем значимости 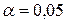 , окончательно принять или отвергнуть выдвинутую гипотезу о распределении генеральной совокупности.
, окончательно принять или отвергнуть выдвинутую гипотезу о распределении генеральной совокупности.
8. Построить на одном чертеже:
| а) | полигон относительных частот 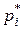 и кривую распределения и кривую распределения  . Сравнить график . Сравнить график  с графиком идеально нормального распределения; с графиком идеально нормального распределения;
|
| б) | гистограмму теоретических вероятностей (относительных частот)  и график и график 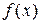 . .
|
9. Найти доверительные интервалы для генеральной средней и генерального среднего квадратического отклонения по уровню надёжности 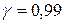 .
.
|
|
|
|
|
Дата добавления: 2015-06-26; Просмотров: 1412; Нарушение авторских прав?; Мы поможем в написании вашей работы!