Геометрический способ сложения сил

Геометрический способ определение равнодействующей системы сходящихся сил.

Аксиома о равновесии

Свободное тело – это тело, перемещение которого другими телами не ограничено. Если использовать приём образности мышления, то свободное тело мысленно можно представлять в виде воздушного шара, птицы в полёте, вертолёта, подводной лодки и т.п.

Понятие «равновесие свободного тела» (кратко: «равновесие тела») в полном своём объёме требует знаний кинематики, но в инженерной практике чаще предстаёт в форме покоя тела. Поэтому, при изучении статики можно считать, что «равновесие тела» - это его покой.

Аксиома о равновесии: если главные вектор и момент всех приложенных к телу сил равны нулю, то такое тело находится в равновесии. Справедливо и обратное утверждение – если тело находится в равновесии, то главные вектор и момент всех действующих на него сил равны нулю. Уместно вспомнить:

1) результат 12.18- равенство нулю главного момента не зависит от выбора центра, относительно которого он вычисляется;

2) результат 13.2 - при рассмотрении аксиомы о равновесии достаточно учитывать лишь внешние силы.

Называют:

уравновешенная система сил - это система сил с нулевыми главными вектором и моментом.

Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сло­жением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил 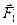, , …, 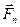(рис. 14, a), откладываем от произвольной точки О (рис. 14, б) век­тор Oa, изображающий в выбранном масштабе cилу F ₁, от точки a откладываем вектор , изображающий силу F ₂, от точки b откла­дываем вектор bc, изображающий силу F ₃ и т. д.; от конца m пред­последнего вектора откладываем вектор mn, изображающий силу F _n.Соединяя начало первого вектора с концом последнего, получаем вектор 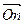= 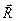, изображающий геометрическую сумму или главный вектор слагаемых сил:

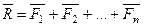или

От порядка, в котором будут откладываться векторы сил, модуль и направление 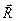не зависят. Легко видеть, что проделанное по­строение представляет собою результат последовательного приме­нения правила силового тре­угольника.

Рис.14

Фигура, построенная на рис. 14, б, называется силовым (в общем случае векторным) многоугольником. Таким обра­зом, геометрическая сумма или главный вектор несколь­ких сил изображается замы­кающей стороной силового многоугольника, построенно­го из этих сил (правило сило­вого многоугольника). При построении векторного многоугольника следует помнить, что у всех слагаемых векторов стрелки должны быть направлены в одну сторону (по обводу многоугольника), а у вектора 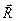- в сторону противоположную.

Равнодействующая сходящихся сил. При изучении статики мы будем последовательно переходить от рассмотрения более простых систем сил к более сложным. Начнем с рассмотрения си­стемы сходящихся сил. Сходящимися называются силы, линии дей­ствия которых пересекаются в одной точке (см. рис. 14, а).

По следствию из первых двух аксиом статики система сходящихся сил, действующих на абсолютно твердое тело, эквивалентна системе сил, приложенных в одной точке (на рис. 14, а в точке А).

Последовательно применяя аксиому параллелограмма сил, прихо­дим к выводу, что система сходящихся сил имеет равнодей­ствующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке их пересечения. Следовательно, если силы 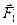, , …, 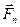сходятся в точке A (рис. 14, а), то сила, равная главному вектору 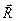, найденному построением силового мно­гоугольника, и приложенная в точке А, будет равнодействующей этой системы сил.

Дата добавления: 2015-06-04