Основные понятия

В медицинской практике

Дифференциальные уравнения и их применение

Дифференциальные уравнения являются мощнейшим математическим аппаратом для изучения процессов, протекающих в природе.

Приведем примеры дифференциальных уравнений, описывающих физические процессы:

1) Второй закон Ньютона 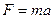можно записать, используя дифференциальные уравнения:

, , ;

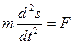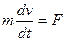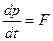2) уравнение радиоактивного распада 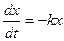(k – постоянная распада, х – количество неразложившегося вещества в момент времени t, скорость распада 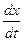пропорциональна количеству распадающегося вещества).

3) Основной закон электромагнитной индукции записывается в виде дифференциального уравнения: 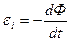и т. д.

Дифференциальное уравнение – это уравнение, содержащее производные от искомой функции или ее дифференциалы.

В дифференциальном уравнении неизвестной является функция, входящая в уравнение под знаками производных (или дифференциалов) того или иного порядка.

Порядком дифференциального уравнения называется порядок старшей производной или дифференциала, содержащегося в этом уравнении.

Общий вид дифференциального уравнения n -го порядка следующий: 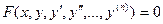, причем в частных случаях в это уравнение могут не входить x, y и отдельные производные порядка ниже, чем n.

Если искомая функция 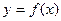есть функция одного аргумента, то дифференциальное уравнение называется обыкновенным. Если же искомая функция зависит от нескольких аргументов и дифференциальное уравнение содержит ее частные производные по этим аргументам, то оно называется дифференциальным уравнением в частных производных.

Дифференциальное уравнение называется линейным, если его левая часть есть многочлен первой степени относительно неизвестной функции y и ее производных (и не содержит их произведений), т. е. если это уравнение имеет вид

.

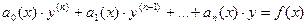Здесь функции , обычно определенные и непрерывные в некотором общем интервале, называются коэффициентами линейного уравнения, а функция – правой частью или свободным членом.

Если правая часть линейного уравнения тождественно равна нулю, то уравнение называется однородным (или без правой части), в противном случае это уравнение называется неоднородным (или с правой частью).

Решением дифференциального уравнения называется всякая функция 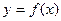, которая, будучи подставлена в исходное дифференциальное уравнение, обращает его в тождество.

Например, решением уравнения теплопроводности (уравнения в частных производных) является функция .

Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения.

Различают общее и частное решения дифференциального уравнения.

Общим решением дифференциального уравнения называется такое его решение 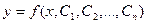, которое содержит столько независимых произвольных постоянных , каков порядок этого уравнения.

Произвольные постоянные называются независимыми, если общее число постоянных, входящих в состав функции f, не может быть уменьшено путем введения других произвольных постоянных.

Если общее решение дифференциального уравнения получают в неявном виде 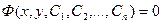, то оно называется общим интегралом.

Отыскание частного решения (частного интеграла) дифференциального уравнения n -го порядка (n = 1,2,3,…), удовлетворяющего n начальным условиям вида , , 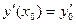,…, , называется задачей Коши.

Геометрически каждому частному решению дифференциального уравнения соответствует график общего решения – плоская линия, которая называется интегральной кривой этого уравнения, а общему решению соответствует совокупность (семейство) всех интегральных кривых.

Рассмотрим методы решения некоторых типов дифференциальных уравнений.

Решение дифференциальных уравнений первого порядка с разделяющимися переменными

К таким уравнениям относятся уравнения вида

.

Путем алгебраических преобразований данное уравнение приводят к уравнениям вида , называемым уравнениями с разделенными переменными. Функции 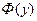, 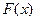считают непрерывными.

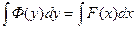
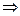
После интегрирования уравнения находим общее решение дифференциального уравнения или общий интеграл: 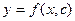. Здесь 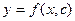– общее решение.

Дата добавления: 2015-06-26