Центр параллельных сил

Для прямоугольника линия действия силы проходит через точку пересечения его диагоналей, а в случае треуголь­ника через точку пересечения его медиан.

Рассматривая сложение параллельных сил в п. 16, мы показали, что система параллельных сил приводится к равнодействующей (F₁, F₂,..., F_n) ~ R*.

Центром параллельных сил называется точка, через которую проходит эта равнодействующая при любых поворотах системы параллельных сил в пространстве. 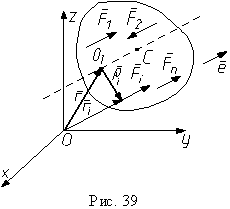Докажем, что центр параллельных сил существует и определим его координаты. Пусть система параллельных сил, эквивалентная равнодействующей, действует на твердое тело, а Q₁ - какая-либо точка на линии действия равнодействующей. Пусть так же r - радиус-вектор точки Q₁, а r_i - радиус-вектор точки приложения силы F_i (рис. 39). Вычислим сумму моментов всех сил системы относительно точки Q₁. Для этого построим радиус-вектор ρ_i, соединяющий точку Q₁ с точкой приложения силы F_i. Тогда

Но по рис. 39 r_i = r + ρ_i и ρ_i = r_i - r, следовательно,

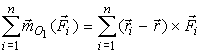
(1)

Введем единичный вектор e, параллельный силам. Тогда любая сила системы может быть выражена как

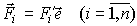
(2)

где F_i' - проекция силы на направление единичного вектора, имеющая свой знак.

По рис. 39, например, F₁' положительна, а F₂' отрицательна. Подставляя в правую часть равенства (1) выражение (2), приписав в ней скалярный множитель к первому сомножителю векторного произведения, вынеся e за знак суммы, получаем

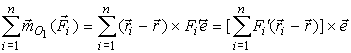
(3)

Для нахождения центра параллельных сил воспользуемся теоремой Вариньона. По теореме сумма моментов всех сил системы относительно точки O₁ должна быть равна нулю, так как точка O₁ лежит на линии действия равнодействующей R*:

(4)

Поэтому из (3) имеем

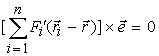
(5)

Так как e 0, то последнее равенство выполняется при любых поворотах системы сил и единичного вектора e только тогда, когда выражение в квадратных скобках равно нулю:

(6)

В свою очередь равенство (6) имеет единственное решение для радиус-вектора r, которое определяет положение центра параллельных сил, чем доказывается само существование центра параллельных сил. Обозначив центр параллельных сил точкой C (рис. 39), определим из уравнения (6) его радиус-вектор r_C:

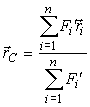
(7)

Находим координаты центра параллельных сил, введя систему координат OXYZ с началом в O, проектируя на ее оси выражение (7):

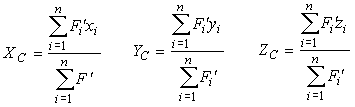
(8)

В формулах (8) x_i, y_i, z_i являются координатами точек приложения сил системы, следовательно, числителями и знаменателями дробей будут алгебраические суммы.

Отметим, что выбор направления e, вдоль которого параллельные силы считаются положительными, произволен и не влияет на результаты вычисления координат центра параллельных сил (X_C, Y_C, Z_C) по формулам (8).

Дата добавления: 2015-06-04