Центр масс тела. Равновесие. Масса тела

Любое тело можно рассматривать как совокупность материальных точек, в качестве которых можно, например, брать молекулы. Пусть тело состоит из n материальных точек с массами m1, m2,...mn.

Центром масс тела, состоящего из n материальных точек, называется точка (в геометрическом смысле), радиус-вектор которой определяется формулой:

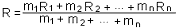
Здесь R1 – радиус-вектор точки с номером i (i = 1, 2,... n).

Это определение выглядит непривычно, но на самом деле оно даёт положение того самого центра масс, о котором у нас имеется интуитивное представление. Например, центр масс стержня будет находиться в его середине. Сумма масс всех точек, входящая в знаменатель вышеопределённой формулы, называется массой тела. Массой тела называется сумма масс всех его точек: m = m1 + m2 +... + mn.

В симметричных однородных телах ЦМ всегда расположен в центре симметрии или лежит на оси симметрии, если у фигуры центра симметрии нет. Центр масс может находиться как внутри тела (диск, квадрат, треугольник), так и вне его (кольцо, рамка, угольник).

25. Координаты центров тяжести неоднородных тел.

Координаты центра тяжести неоднородного твердого тела в выбранной системе отсчета определяются следующим образом:

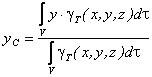
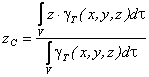
где 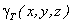- вес единицы объема тела (удельный вес)

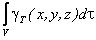- вес всего тела.

Если твердое тело представляет собой неоднородную поверхность, то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:

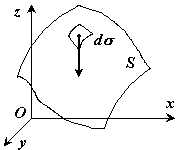
где - вес единицы площади тела,

- вес всего тела.

Если твердое тело представляет собой неоднородную линию, то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:

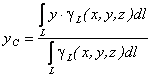
где 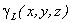- вес единицы длины тела,

- вес всего тела.

Дата добавления: 2015-06-04