Основная теорема статики

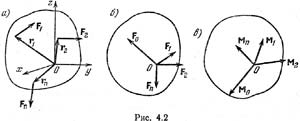
Пусть дана произвольная система сил (F₁, F₂,..., F_n). Сумму этих сил F=åF_k называют главным вектором системы сил. Сумму моментов сил относительно какого-либо полюса называют главным моментом рассматриваемой системы сил относительно этого полюса.

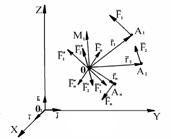
Осн теор статики (теорема Пуансо): Всякую пространственную систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы, прило­женной в какой-либо точке тела (центре приведения) и равной глав­ному вектору данной системы сил, и одной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра приведения. Пусть О — центр приведения, принимаемый за начало коорди­нат, r₁,r₂, r₃,…, r_n–соответствующие радиусы-векторы точек приложения сил F₁, F₂, F₃,...,F_n, составляющих данную систему сил (рис. 4.2, а). Перенесем силы F₁, F_a, F₃,..., F_n в точку О. Сложим эти силы как сходящиеся; получим одну силу: F_о=F₁+F₂+…+F_n=åF_k, которая равна главному вектору (рис. 4.2, б). Но при последователь­ном переносе сил F₁, F₂,..., F_n в точку О мы получаем каждый раз соответствующую пару сил (F₁, F”₁), (F₂,F”₂),...,(F_n, F"_n).Моменты этих пар соответственно равны моментам данных сил относительно точки О: М₁=М(F₁,F”₁)=r₁ x F₁=М_о(F₁), М₂=М(F₂, F”₂)=r₂ x F₂=М_о(F₂), …, М_п=М(F_n, F"_n)=r_n x F_n=М_о(F_n). На основании правила приведения системы пар к простейшему виду все указанные пары можно заменить одной парой. Ее момент равен сумме моментов всех сил системы относительно точки О, т. е. равен главному моменту, так как согласно формулам (3.18) и (4.1) имеем (рис. 4.2, в) М₀=М₁+М₂+...+М_n=М_о(F₁)+М_о(F₂)+…+ М_о(F_n)==åМ_о(F_k)=år_k x F_k. Систему сил, как угодно расположенных в пространстве, можно в произвольно выбранном центре приведения заменить силой F_o=åF_k (4.2) и парой сил с моментом M₀=åM₀(F_k)=år_k x F_k. (4.3). В технике очень часто проще задать не силу или пару, а их моменты. Например, в характеристику электромотора входит не сила, с которой статор действует на ротор, а вращающий момент.

16/18. Приведение произвольной пространственной системы сил к данному центру. Главный вектор и главный момент. Систему сил, приложенных к телу, можно упростить, используя теорему о параллельном переносе силы. В результате приведения произвольной пространственной системы сил к данному центру в общем случае получаем главный вектор, равный геометрической сум-ме всех сил системы, и главный момент, равный геометрической сумме момен-тов всех приводимых сил относительно центра приведения (рис. 1.33).
Сложим и т.д., получим силовой многоугольник, где

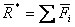(1.15)
Затем векторно сложим векторы моментов
(1.16)

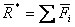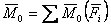; (1.17)

Главный вектор инвариантен по отношению к центру приведения. Главный момент зависит от вы-бора центра приведения. По модулю главный вектор вычисляется

R*= (1.18)

Рис. 1.33

где

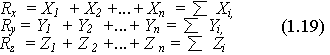
проекции главного вектора на координатные оси 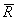*(Rx, Ry, Rz), а проекции каждой из сил (X1, Y1, Z1), (X2, Y2, Z2) и т.д.
Направление находим по направляющим косинусам

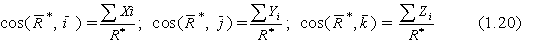
Главный момент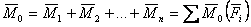

Для равновесия произвольной пространственной системы сил необходимо и дос-таточно, чтобы алгебраическая сумма проекций всех этих сил на каждую из коор-динатных осей равнялась нулю, и чтобы алгебраическая сумма моментов всех сил системы относительно каждой из трех координатных осей равнялась нулю.

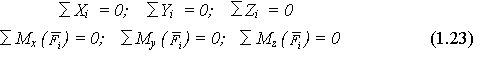
Система параллельных сил. Если ось OZ параллельна силам, то три уравнения (1.23) обращаются в тождества, так как проекции сил на оси OX и OY и их моменты относительно оси OZ равны нулю. Оставшиеся три уравнения явля-ются уравнениями равновесия параллельных сил в пространстве (рис. 1.34).

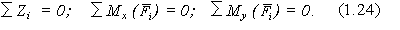
Для параллельных сил расположенных в плоскости XOY (рис. 1.35), имеем два уравнения равновесия:

(1.25)

17./18 Плоская система произвольно расположенных сил. Если силы дейст-вуют в плоскости XOY (рис. 1.36), то суммы проекций их на ось OZ и моментов относительно осей OX и OY равны нулю. При равновесии тела под действием плоской системы сил суммы их про-екций на оси координат и сумма моментов относительно произвольного центра, лежащего в плоскости сил, равны нулю

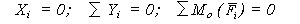
Рис. 1.34 Рис. 1.35 Рис. 1.36 Примеры упрощения системы сил, действующих на самолет. Силы взаимодействия самолета с поверхностью взлетно-посадочной полосы (ВПП) и воздухом при движении по земле и в полете подчиняются сложным закономер-ностям. Во всех случаях систему сил, действующих на самолет, упрощают. На-пример, воздушное давление, неравномерно распределенное по нижней и верх-ней поверхностям крыла (или стабилизатора, киля), часто суммируют и относят к одной поверхности. Силы, действующие на самолет в горизонтальном полете с постоянной скоростью без бокового ветра, могут быть приведены к плоской системе сил (рис. 1.37).

Рис.

1.37

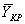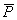Вес самолета , подъемная сила крыла и горизонтального оперения , тяга двигателей и сила лобового сопротивления 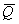удовлетворяют трем уравнениям равновесия:
1) условие сохранения постоянной скорости

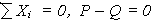(1.27)

2) условие сохранения постоянной высоты

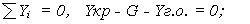(1.28)

3) условие сохранения горизонтального положения самолета

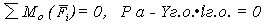(1.29)

20. Параллельные силы

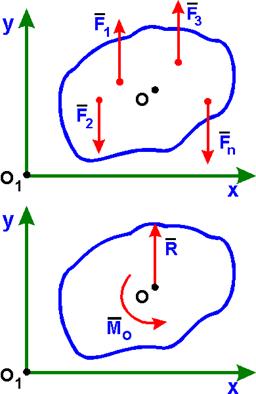Система сил F₁, F₂,..., F_n, лежащих в одной плоскости, линии действия которых параллельны друг другу, называется плоской системой параллельных сил.

При приведении этой системы сил к произвольному центру (точке) О получим главный вектор R, приложенный в точке О, и пару сил с моментом M_o.

Главный вектор R системы параллельных сил параллелен силам, его модуль равен абсолютномузначению алгебраической суммы проекций сил на ось (О₁у), параллельную силам, а его направление определяется знаком этой суммы:

| R | = | R_y | = |S± F_k |. (k = 1, 2,..., n)

Момент пары сил M_o равен главному моменту параллельных сил F₁, F₂,..., F_n относительно центра приведения О:

M_o = S m_o(F_k). (k = 1, 2,..., n)

Условия равновесия для плоской системы параллельных силимеют вид:

R = 0, M_o = 0.

Из них следуют две формы аналитических условий равновесия для системы параллельных сил на плоскости.

1. Основная форма условий равновесия.

S F_ky = S±F_ky = 0, S m_o(F_k) = 0. (k = 1, 2,..., n)

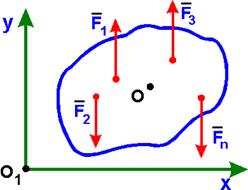для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы сумма проекций сил на ось, параллельную силам, и сумма их моментов относительно точки, лежащей на плоскости действия сил, были равны нулю.

2. Вторая форма условий равновесия:

S m_А(F_k) = 0, S m_В(F_k) = 0. (k = 1, 2,..., n)

Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы суммы моментов всех сил относительно любых двух точек А и В (причем прямая АВ не параллельна силам), были равны нулю.

Для плоской системы параллельных сил каждая форма содержит два уравнения равновесия.

Дата добавления: 2015-06-04