Аналитические выражения для моментов силы относительно осей системы координат

Для правила сложения моментов сил различают два случая

1. Моменты сил лежат в одной плоскости, оси вращения параллельны. Их сумма определяется путем алгебраического сложения. Правовинтовые моменты входят в сумму со знаком минус. Левовинтовые — со знаком плюс

2. Моменты сил лежат в разных плоскостях, оси вращения не параллельны. Сумма моментов определяется путем геометрического сложения векторов.

Из-за важности вычисления моментов относительно осей системы координат рассмотрим, как их можно вычислить аналитически.

Для получения этих выражений используем формулу (1). Вводим систему координат с началом в центре - точке O. Выражаем вектор-момент относительно центра в проекциях на оси введенной системы координат OXYZ. Учитывая, что проекции радиус-вектора на оси координат являются координатами точки приложения силы, раскрываем определитель векторного произведения, элементами которого являются единичные векторы и проекции векторов на оси координат:

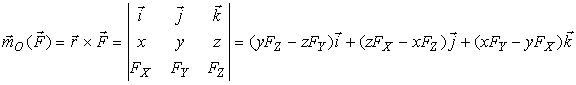
Выражения перед единичными векторами являются проекциями вектора-момента на оси координат. Учитывая выражения (8), получаем аналитические выражения для моментов силы относительно осей системы координат OXYZ:

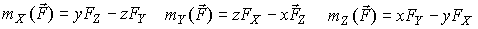
(9)

В заключение параграфа еще раз подчеркнем, что момент силы физически отражает возможность силы поворачивать твердое тело, а математически, как оказалось, определяет линию действия силы самым удобным для практического применения способом. Иными словами, в общем случае, изучая действие сил на твердое тело, нужно, как с физической, так и с математической точки зрения учитывать не только сами силы, но и моменты этих сил.

10.Сложение ПАР сил.Условия равновесия пар сил.

Системой пар сил является совокупность пар сил, приложенных к одному телу.

Сложение пар сил. Система пар сил эквивалентна одной паре, момент которой равен сумме моментов пар, образующих систему:

(8)

где M₁ = M(F₁,F₁'), M₂ = M(F₂,F₂'),..., M_n = M(F_n,F_n').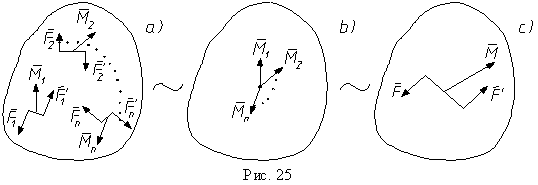

На рис. 25, a представлена исходная система пар сил. По второму свойству заменяем пары их моментами и переносим моменты пар, как свободные векторы, в одну произвольную точку (рис. 25, b). По правилу параллелограмма мы складываем векторы моментов пар и получаем второе выражение в (8). Одному моменту пары M соответствует одна пара сил (F,F') и M = M(F,F') (рис. 25, c).

Если все пары лежат в одной плоскости, векторное суммирование моментов пар теряет смысл. Поэтому мы используем алгебраические моменты пар сил и получаем

(9)

Равновесие системы пар. Вначале сформулируем, а затем докажем условие равновесия для системы пар сил.

Для равновесия твердого тела под действием системы пар сил необходимо и достаточно, чтобы геометрическая сумма моментов пар, образующих систему, была равна нулю:

(10)

Необходимость условия сразу следует из (8). Если M = 0, то (F,F') ~ 0 и, следовательно, ((F₁,F'₁), (F₂,F'₂),..., (F_n,F'_n)) ~ 0. Достаточность условия докажем методом от противного. Предположим, что условие (10) не выполняется и M 0, а твердое тело находится в равновесии. В этом случае система пар сил приводится к одной паре (F,F') и тело в равновесии находиться не может. Таким образом, наше предположение не верно, а условие (10) является верным, и его достаточность доказана.

Необходимым и достаточным условием равновесия системы пар, лежащих в одной плоскости, является равенство нулю алгебраической суммы моментов всех пар системы:

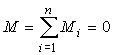
(11)

Таким образом, в этом параграфе мы рассмотрели пару сил, являющуюся, как и сила, самостоятельным элементом статики, изучили свойства пары сил, эквивалентность пар, сложение и условия равновесия для системы пар сил.

11. Момент пары сил

Вектор момента пары сил 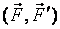направлен перпендикулярно плоскости действия пары сил в ту сторону, откуда вращение тела парой сил наблюдается происходящим против часовой стрелки (рис. 2.2).

Модуль момента пары сил равен произведению модуля одной из сил пары на ее плечо, т. е. .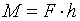

Рис. 2.2. Момент пары сил

Рис. 2.3. Проекции векторного момента пары сил на оси координат

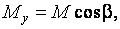
Векторный момент пары сил, произвольно расположенный в декартовой системе координат , может быть представлен в разложении по этим осям координат (рис. 2.3), , где 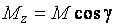– проекции векторного момента 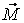на соответствующие оси координат.

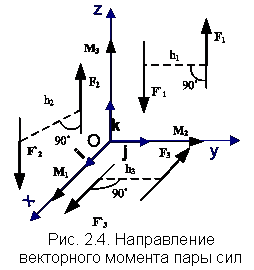
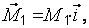
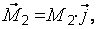
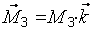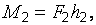
Векторный момент пары сил, расположенный в одной из координатных плоскостей, или ей параллельной, следует приложить в цент­ре , направив вдоль соответствующей оси в сторону, откуда вращение тела парой сил представляется против часовой стрелки (рис. 2.4). Так , где – модули моментов соответствующих пар сил.

Известно, что пару сил можно как угодно поворачивать и переносить в плоскости ее действия; от этого действие пары сил на твердое тело не изменяется, если алгебраический момент пары сил остается таким же. Следовательно, векторный момент пары сил можно переносить параллельно самому себе в любую точку твердого тела, лежащую в плоскости действия пары сил. Так как к тому же пару сил можно переносить в параллельную плоскость, то векторный момент пары сил можно переносить параллельно самому себе в любую точку тела, не изменяя действия пары сил на твердое тело. [2]

Если на тело действуют несколько пар сил и эти пары лежат в одной плоскости, то векторы моментов пар параллельны и вместо них можно рассматривать алгебраические моменты. Алгебраический момент пары сил равен взятому с определенным знаком произведению модуля одной из сил пары на ее плечо. [3]

Дата добавления: 2015-06-04