Теоремы о парах

Теоремы о парах

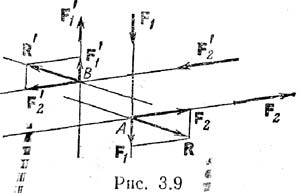
Теорема 1. Две пары, лежащие в одной плоскости, можно заменить одной парой, лежащей в той же плоскости, с моментом, равным сумме моментов данных двух пар. Для док–ва рассмотрим две пары (F₁, F`<sub>1</sub>) и (F<sub>2</sub>, F`₂) (рис. 3.9) и перенесем точки приложения всех сил вдоль линий их действия в точки А и В соответственно. Складывая силы по аксиоме 3, получим R=F₁+F₂ и R'=F`<sub>1</sub>+F`₂, но F'₁=–F₁ и F`<sub>2</sub>=–F<sub>2</sub>. Следовательно, R=–R', т. е. силы R и R' образуют пару. Момент этой пары: М=М(R, R')=ВАxR=BAx(F<sub>1</sub>+F<sub>2</sub>)=ВАxF<sub>1</sub>+ВАxF<sub>2</sub>. (3.14). При переносе сил, составляющих пару, вдоль линий их действия ни плечо, ни направление вращения пары не меняются, следовательно, не меняется и момент пары. Зна­чит, ВАхF<sub>1</sub>=M(F<sub>1</sub>, F'<sub>1</sub>)=M<sub>1</sub>, ВАxF<sub>2</sub>=M(F<sub>2</sub>, f`₂)=M₂, и формула (З.14) примет вид M=M₁+M₂, (3.15) ч.т.д. Сделаем два замечания. 1. Линии действия сил, составляющих пары, могут оказаться параллельными. Теорема остается справедливой и в этом случае. 2. После сложения может получиться, что М(R,R')=0; на основании замечания1 из этого следует, что сово­купность двух пар (F₁, F`<sub>1</sub>, F<sub>2</sub>, F`₂)~0.

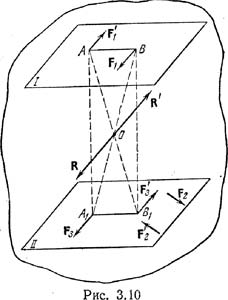
Теорема 2. Две пары, имеющие равные моменты, эквивалентны. Пусть на тело в плоскости I действует пара (F₁,F`<sub>1</sub>) с моментом M<sub>1</sub>. Покажем, что эту пару можно заменить другой парой (F<sub>2</sub>, F`₂), расположенной в плоскости II, если только ее момент М₂ равен М₁. Заметим, что пло­скости I и II должны быть параллельны, в частности, они могут совпадать. Действительно, из параллельности моментов M₁, и М₂ следует, что плоскости действия пар, перпендикулярные моментам, также параллельны. Введем в рассмотрение новую пару (F₃, F`<sub>3</sub>) и приложим ее вместе с парой (F<sub>2</sub>, F`₂) к телу, расположив обе пары в плоскости II. Для этого согласно аксиоме 2 нужно подобрать пару (F₃, F`<sub>3</sub>) с мо­ментом М<sub>3</sub> так, чтобы приложенная система сил (F<sub>2</sub>, F`₂, F₃, F`<sub>3</sub>) была уравновешена. Положим F<sub>3</sub>=–F`₁ и F`<sub>3</sub>=–F<sub>1</sub> и совместим точки при­ложения этих сил с проекциями А<sub>1</sub> и B<sub>1</sub> точек А и В на плоскость II (см. рис. 3.10). В соответствии с построением будем иметь: М<sub>3</sub>=–M<sub>1</sub> или, учитывая, что М<sub>1</sub>=М<sub>2</sub>, М<sub>2</sub>+М<sub>3</sub> = 0, получим (F<sub>2</sub>, F`₂, F₃, F`<sub>3</sub>)~0. Т.о., пары (F<sub>2</sub>, F`₂) и (F₃, F`<sub>3</sub>) взаимно уравновешены и присоединение их к телу не нару­шает его состояния (аксиома 2), так что (F<sub>1</sub>, F`₁)~(F₁, F`<sub>1</sub>, F<sub>2</sub>, F`₂, F₃, F`<sub>3</sub>). (3.16). С другой стороны, силы F<sub>1</sub> и F<sub>3</sub>, а также F`₁ и F`<sub>3</sub> можно сло­жить по правилу сложения параллельных сил, направленных в одну сторону. Они равны по модулю, поэтому их рав­нодействующие R и R' должны быть приложены в точке пересече­ния диагоналей прямоугольника ABB<sub>1</sub>A<sub>1</sub>, кроме того, они равны по модулю и направлены в проти­воположные стороны. Это означает, что они составляют систему, экви­валентную нулю. Итак, (F<sub>1</sub>, F`₁, F₃, F`<sub>3</sub>)~(R, R')~0. Теперь можем записать (F<sub>1</sub>, F`₁, F₂, F`<sub>2</sub>, F<sub>3</sub>,F`₃)~(F₂, F`<sub>2</sub>).(3.17). Сравнивая соотношения (3.16) и (3.17), получим (F<sub>1</sub>, F`₁)~(F₂, F`₂), ч.т.д. Из этой теоремы следует, что пару сил можно перемещать и поворачивать в плоскости ее действия, переносить в параллельную плоскость; в паре можно менять одновременно силы и плечо, сохраняя лишь направление вращения пары и модуль ее момента (F₁h₁=F₂h₂).

Дата добавления: 2015-06-04