Центр тяжести

Рассмотрим тело у поверхности Земли. На каждую малую часть тела объема v_i действует сила тяжести p_i, с которой эта часть взаимодействует с Землей. Силы тяжести направлены к центру Земли и образуют систему сходящихся сил. Но радиус Земли намного больше размеров тел, находящихся на ее поверхности, и систему сил тяжести (p₁, p₂,..., p_n) можно принять за систему параллельных сил, направленных по вертикали вниз (рис. 40, где ось OZ направлена по вертикали вверх). Равнодействующая этой системы сил P названа силой тяжести тела, ее модуль равен весу тела и определяется равенством

(9)

Силы p_i при любых поворотах тела остаются приложенными в одних и тех же точках тела и параллельными друг другу, изменяется только их направление по отношению к телу. Следовательно, равнодействующая P этих сил всегда будет проходить через одну и ту же точку C, которая названа центром тяжести.

Таким образом, центром тяжести является точка, через которую проходит сила тяжести тела, находящегося у поверхности Земли, при любых поворотах тела относительно Земли.

Положение центра тяжести определяется по формулам (7), (8) для центра параллельных сил с учетом того, что элементарные силы тяжести направлены в одну сторону и их проекции на направление e положительны (рис. 40) и равны модулям этих сил p_i' = p_i:

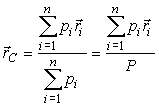
	(10)
	(11)

Учтем удельный вес (вес единицы объема). Для однородных тел он одинаковый во всех точках тела, а для неоднородных различен в каждой точке.

Поэтому для однородных тел p_i = w_i и

где γ - удельный вес, а V - объем всего тела. Подставив последние выражения в (10) и (11), получаем формулы центра тяжести объема:

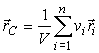
	(12)
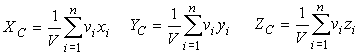
	(13)

Из полученных формул видно, что положение центра тяжести однородного тела зависит только от его геометрической формы. По этой причине точку C и называют центром тяжести объема.

У тонких однородных поверхностей (пластины, листы, сферы и т.д.) и однородных линий (канаты, проволока) веса единицы площади или длины так же одинаковы во всех точках. Поэтому из формул (12) и (13) можно определить положения центров тяжести поверхности или линии.

Обозначая как s_i и S площадь части поверхности и всю ее площадь, найдем по формулам (13) координаты центра тяжести поверхности:

(14)

Если вся поверхность лежит в одной плоскости, например в плоскости OXY, то в формулах (14) все z_i = 0 и Z_C = 0, а координаты X_C и Y_C определяют положение центра тяжести площади.

Обозначая, как l_i и L длину части линии и всю ее длину, находим по формулам (13) координаты центра тяжести линии:

(15)

Рассмотрим неоднородное тело, у которого p_i = γ_iv_i, где γ_i - удельный вес малой части тела, имеющей во всех точка объема v_i одинаковый удельный вес. Подставляя последнее выражение в формулы (11), можно определить координаты центра тяжести неоднородного тела.

Дата добавления: 2015-06-04