Центры тяжести некоторых одно­родных тел

Способы определения координат центра тяжести.

Исходя из полученных выше общих формул, можно указать конкретные способы определения координат центров тяжести тел.

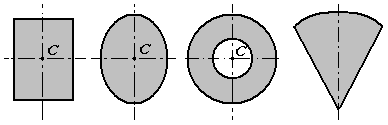
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

2. Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести и площадь известны.

.

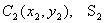
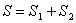3. Дополнение. Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.

.

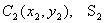
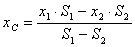
1) Центр тяжести дуги окруж­ности. Рассмотрим дугу АВ радиуса R с центральным углом . В силу сим­метрии центр тяжести этой дуги лежит на оси Ox (рис. 37).

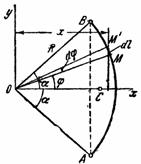
Рис.37

Найдем координату 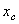по формуле 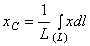. Для этого выделим на дуге АВ элемент ММ’ длиною 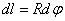, положение которого определяется углом 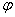. Координата х элемента ММ’ будет . Подставляя эти значения х и 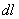и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:

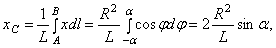
где L - длина дуги АВ, равная 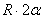. Отсюда окончательно нахо­дим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном

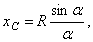
где угол 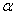измеряется в радианах.

2) Центр тяжести площади тре­угольника. Разобьем площадь треуголь­ника ABD (рис. 38) прямыми, параллель­ными AD, на узкие полоски; центры тяжести этих полосок будут лежать на медиане BE треугольника.

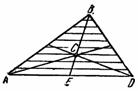
Рис.38

Следовательно, и центр тяжести всего тре­угольника лежит на этой медиане. Аналогичный результат получается для двух других медиан. Отсюда заключаем, что центр тяжести площади треугольника лежит в точке пересечения его медиан.

При этом, как известно,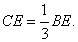

3) Центр тяжести площади кругового сектора. Рассмотрим круговой сектор ОАВ радиуса R с центральным углом 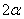(рис. 39). Разобьем мысленно площадь сектора ОАВ радиусами, проведенными из центра О, на п секторов. В пределе, при неограниченном увеличении числа , эти секторы можно рассматривать как плоские треугольники, центры тяжести которых лежат на дуге DE радиуса 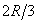. Следовательно, центр тяжести сектора ОAB будет со­впадать с центром тяжести дуги DE. Окончательно получим, что центр тяжести площади кругового сектора лежит на его центральной оси симметрии на расстоянии от начального центра О, равном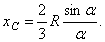

Рис.39

Пример 1. Определим центр тяжести однородного тела, изображён­ного на рис. 40.

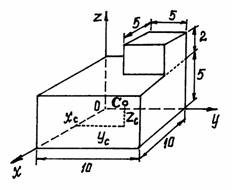
Рис.40

Тело однородное, состоящее из двух частей, имеющих симметричную форму. Координаты центров тяжести их:

Объёмы их: .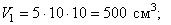

Поэтому координаты центра тяжести тела

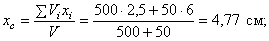
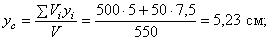
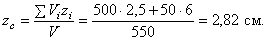
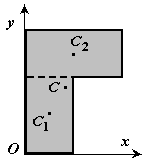
Пример 2. Найдем центр тяжести пластины, согнутой под прямым углом. Размеры – на чертеже (рис.41).

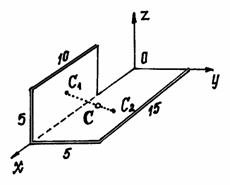
Рис.41

Координаты центров тяжести: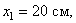

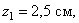
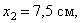
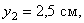
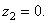
Площади:

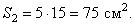
Поэтому:

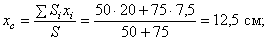
Рис. 6.5.

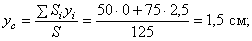
Пример 3. У квадратного листа 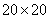см вырезано квадратное отверстие 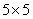см (рис.42). Найдем центр тяжести листа.

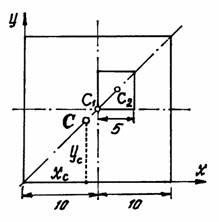
Рис.42

В этой задаче удобнее разделить тело на две части: большой квадрат и квадратное отверстие. Только площадь отверстия надо считать отрицательной. Тогда координаты центра тяжести листа с отверстием:

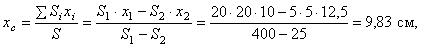
координата 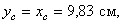так как тело имеет ось симметрии (диагональ).

Пример 4. Проволочная скобка (рис.43) состоит из трёх участков оди­наковой длины l.

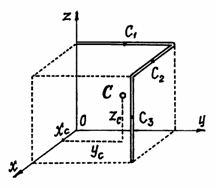
Рис.43

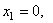
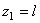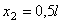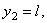
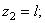
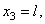
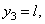
Координаты центров тяжести участ­ков: , ; , Поэтому координаты центра тяжести всей скобки:

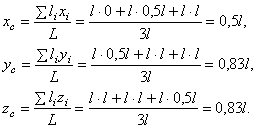
26.

водорода О физическом образовании НОВОСТИ   к учебнику >>

Виды равновесия В механике различают три состояния равновесия: безразличного равновесия, устойчивого и неустойчивого равновесия. Безразличное равновесие - при малом отклонении тело остается в равновесии. Пример - катящееся по горизонтальной поверхности колесо. Если колесо остановить в любой точке, оно окажется в равновесном состоянии. Шар, лежащий на плоской горизонтальной поверхности, находится в состоянии безразличного равновесия (рисунок). Неустойчивое равновесие - при малом отклонение тела из положения равновесия возникают силы, стремящиеся увеличить это отклонение. Шар, находящийся в верхней точке сферического выступа, - пример неустойчивого равновесия. Устойчивое равновесие - если при малых отклонениях тела от этого состояния возникают силы или моменты сил, стремящиеся возвратить тело в равновесное состояние. Шар, находящийся на дне сферического углубления находится в состоянии устойчивого равновесия. 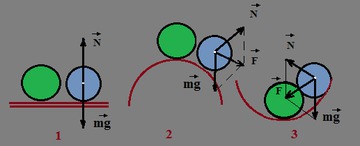Рисунок Различные виды равновесия шара на опоре. (1) - безразличное равновесие, (2) - неустойчивое равновесие, (3) - устойчивое равновесие В неустойчивых системах при малом отклонениях тела от положения равновесия возникают силы, стремящиеся увеличить это отклонение. Атом является неустойчивой системой, т.е при малейшем отклонении электрона вращающегося вокруг протона (увеличение или уменьшение расстояния между протоном и электроном) центростремительные силы увеличивают это отклонение (подробнее см. Википедию).

28.сцепление тел. При увеличении от нуля силы Т, рис.1, стремящейся сдвинуть тело по плоскости, возникает сила сцепления F_сц (иначе – сила трения покоя). Тело будет неподвижным при Т £ F_{сц max}. Коэффициент сцепления (трения покоя) f_сц = F_{сц max} / N, соответствует предельному состоянию равновесия, где N – нормальная реакция плоскости.

Дата добавления: 2015-06-04