Связь между вектором-моментом силы относительно центра и моментом силы относительно оси

Если под действием трех сил твердое тело находится в равновесии и линии действия двух сил пересекаются в одной точке, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.

Теорема о трех силах.

Вначале сформулируем теорему, а затем ее докажем.

Пусть на твердое тело действует система трех сил F₁, F₂ и F₃, причем линии действия первых двух пересекаются в точке A (рис. 11, a). Согласно следствию из второй аксиомы, силы F₁, F₂ переносим в точку A (рис. 11, b). Следуя третьей аксиоме, сложим их, заменив их одной силой, равной R=F₁+F₂. Таким образом, исходная система сил приведена к двум силам R и F₃ (рис. 11, c).

Тело находится в равновесии. Поэтому, по первой аксиоме силы R и F₃ должны иметь общую линию действия. Это может быть только тогда, когда исходные три силы лежат в одной плоскости, а линии действия сил пересекаются в одной точке. Теорема доказана.

Теорема о трех силах позволяет в ряде задач найти линию действия неизвестной силы, приложенной к твердому телу.

7./8 Момент силы относительно центра и оси

Моментом силы относительно центра (обозначается )называется векторное произведение радиус-вектора , проведенного из точки 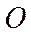в точку приложения силы, на вектор силы (рис. 3.1)

.

Вектор момента направлен перпендикулярно плоскости, в которой лежат сила и точка, в ту сторону, откуда поворот от действия силы виден происходящим против хода часовой стрелки. Вектор момента характеризует положение плоскости и направление вращательного действия силы, а также дает меру этого действия:

, где − плечо силы (кратчайшее расстояние от центра момента до линии действия силы).

Если линия действия силы проходит через центр момента, то ее момент относительно этой точки равен нулю.

Если силы расположены в одной плоскости (плоская система сил), то используется понятие алгебраического момента силы. Алгебраическим моментом силы относительно центра называется взятое со знаком плюс или минус произведение модуля силы на плечо. Знак плюс берется в том случае, если сила стремится поворачивать плоскость относительно центра против хода часовой стрелки (рис. 3.2).

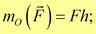
Для характеристики вращательного действия силы на тело, закрепленное на оси, служит момент силы относительно оси (обозначается 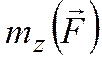)(рис. 3.3). Моментом силы относительно оси называется алгебраическая величина, равная проекции вектора момента силы относительно произвольной точки оси на эту ось: .

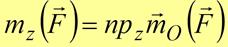Рассмотрим основные способы вычисления момента силы относительно оси.

1. Аналитический

По правилу вычисления векторного произведения:

Откуда

,

,

.

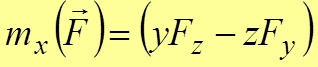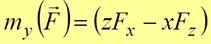2. Геометрический

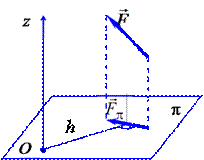
Для вычисления момента силы относительно оси необходимо провести плоскость 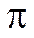(рис. 3.4), перпендикулярную данной оси , спроецировать силу на эту плоскость и вычислить момент проекции 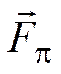относительно точки 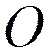− точки пересечения оси с плоскостью 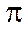. Эквивалентность этих двух способов вытекает из равенств

.

Момент положителен, если, глядя с положительного направления оси, вращение видно происходящим против хода часовой стрелки.

Момент силы относительно оси равен нулю, если сила параллельна оси или линия действия силы пересекает ось.

При вычислении моментов силы относительно координатных осей ее бывает удобно предварительно разложить на составляющие, параллельные координатным осям, и находить момент каждой составляющей отдельно.

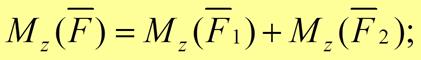
Эта связь отражена в следующем утверждении.

Проекция на ось вектора-момента силы относительно центра на оси равна моменту силы относительно оси.

Математическая запись утверждения, например, для оси Z, имеет вид

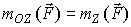
(5)

где m_OZ(F) - проекция вектора m_O(F) на ось Z.

Докажем справедливость этого утверждения. На рис. 20 радиус-вектор r определяет положение точки приложения A силы F относительно центра O, через который проходит ось Z. По определению m_O(F) перпендикулярен плоскости треугольника OAB и, следовательно, его высоте h, которая является и плечом силы. Величина вектора m_O(F) = Fh = 2S_ΔOAB, а его проекция на ось Z равна

(6)

где α - угол между осью Z и вектором-моментом (рис. 20), а S_ΔOAB - площадь треугольника OAB. Величина момента силы относительно оси равна m_Z(F) = F_Пh' = 2S_ΔOA'B'. По рисунку видим, что _ΔOA'B' является проекцией _ΔOAB на плоскость П. Из геометрии известно, что S_ΔOA'B' = S_ΔOAB cosβ, где β - угол между плоскостями треугольников, равный углу между их высотами h и h'. Учитывая последнее равенство, получим

(7)

Но m_O(F) перпендикулярен h, а OZ перпендикулярна h'. Поэтому углы между осью и вектором-моментом и между высотами треугольников равны. При α = β равны правые части равенств (6) и (7), следовательно, равны и левые части, то есть m_OZ(F) = m_Z(F), и утверждение доказано.

Достроим к оси OZ две оси системы координат с началом в центре O. Проведя аналогичные доказательства для осей OX и OY, установим связь между проекциями вектора-момента силы относительно центра и моментами силы относительно осей системы координат с началом в центре:

(8)

На практике вычисление момента силы относительно оси значительно проще нахождения проекции вектора-момента, когда по правилу векторного произведения нужно получить вектор-момент, а затем проектировать его на ось. Поэтому и введено понятие момента силы относительно оси и доказана связь между вектором-моментом и моментом относительно оси, которую мы рассмотрели в этом пункте.

Таким образом, силу, как скользящий вектор, удобнее всего определить шестью параметрами (F_X, F_Y, F_Z, m_X(F), m_Y(F), m_Z(F)). Ранее мы показали, что среди них только пять независимых между собой параметров. Первые три из них - проекции силы на оси координат - определяют величину и направление силы, а моменты силы относительно осей координат определяют линию действия силы.

Понятие момента, впервые введенное в статике для силы, оказалось эффективным и для векторов иной физической природы, и для любых связанных и скользящих векторов. Поэтому понятие момента широко используется в механике и в физике и для других векторов, например, момент количества движения, а в математике понятие момента вектора является основой теории связанных и скользящих векторов.

---СЛОЖЕНИЕ МОМЕНТОВ СИЛ

Дата добавления: 2015-06-04