Механизмы привода режущих аппаратов и их характеристика

2.2.1. Кривошипно-шатунный механизм

Привод ножа у большинства уборочных машин осуществляется кривошипно-шатунным механизмом. Встречаются различные виды этого механизма: плоский ‑ у зерноуборочных комбайнов, пространственный ‑ у косилок, так как брус косилки может совершать колебания не только в вертикально-поперечной плоскости, но и в горизонтальной (до начала работы носок наружного башмака выносят вперед относительно внутреннего). Кроме того, кривошипно-шатунные механизмы делят на центральные (аксиальные), когда ось кривошипного вала лежит на линии движения ножа, и смещенные (дезаксиальные), у которых ось кривошипного вала располагают выше линии движения ножа.

В последнее время для привода режущих аппаратов начали применять и ряд других механизмов: качающуюся шайбу, качающуюся вилку (рис. 2), планетарный механизм, гидропривод, некруглые зубчатые колеса и др.

Применение новых механизмов чаще всего связано со стремлением уменьшить вибрацию машины, возникающую от возвратно-поступательного движения ножа, за счет уменьшения ускорения движущихся масс.

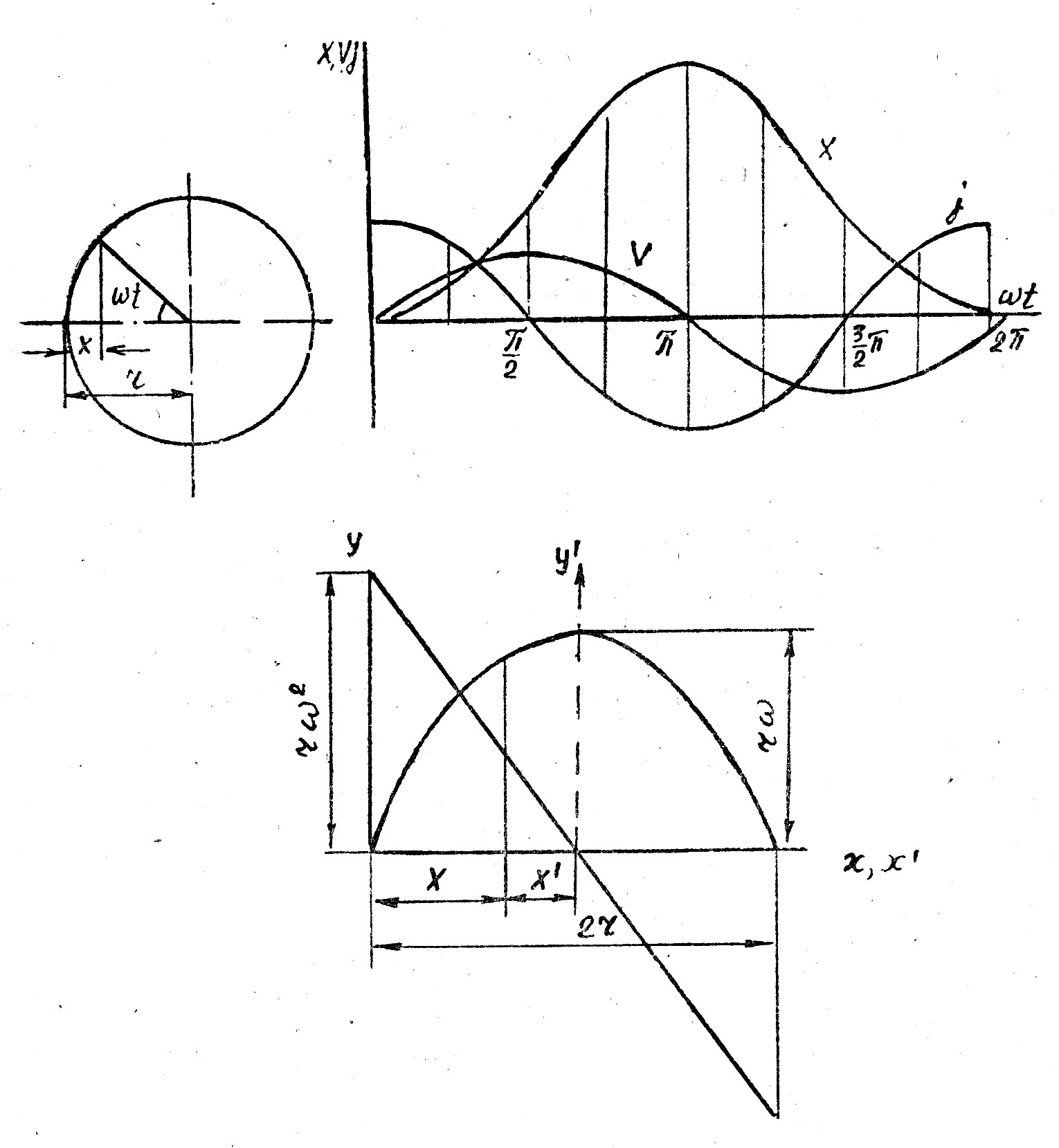
Для обоснования применимости того или иного механизма привода ножа прежде всего необходимо провести анализ кинематических характеристик, таких, как величины перемещений, скоростей и ускорений режущего аппарата в различные моменты процесса резания.

Наиболее простым механизмом, как с точки зрения устройства, так и метода математического описания работы, является плоский центральный кривошипно-шатунный механизм (рис. 2).

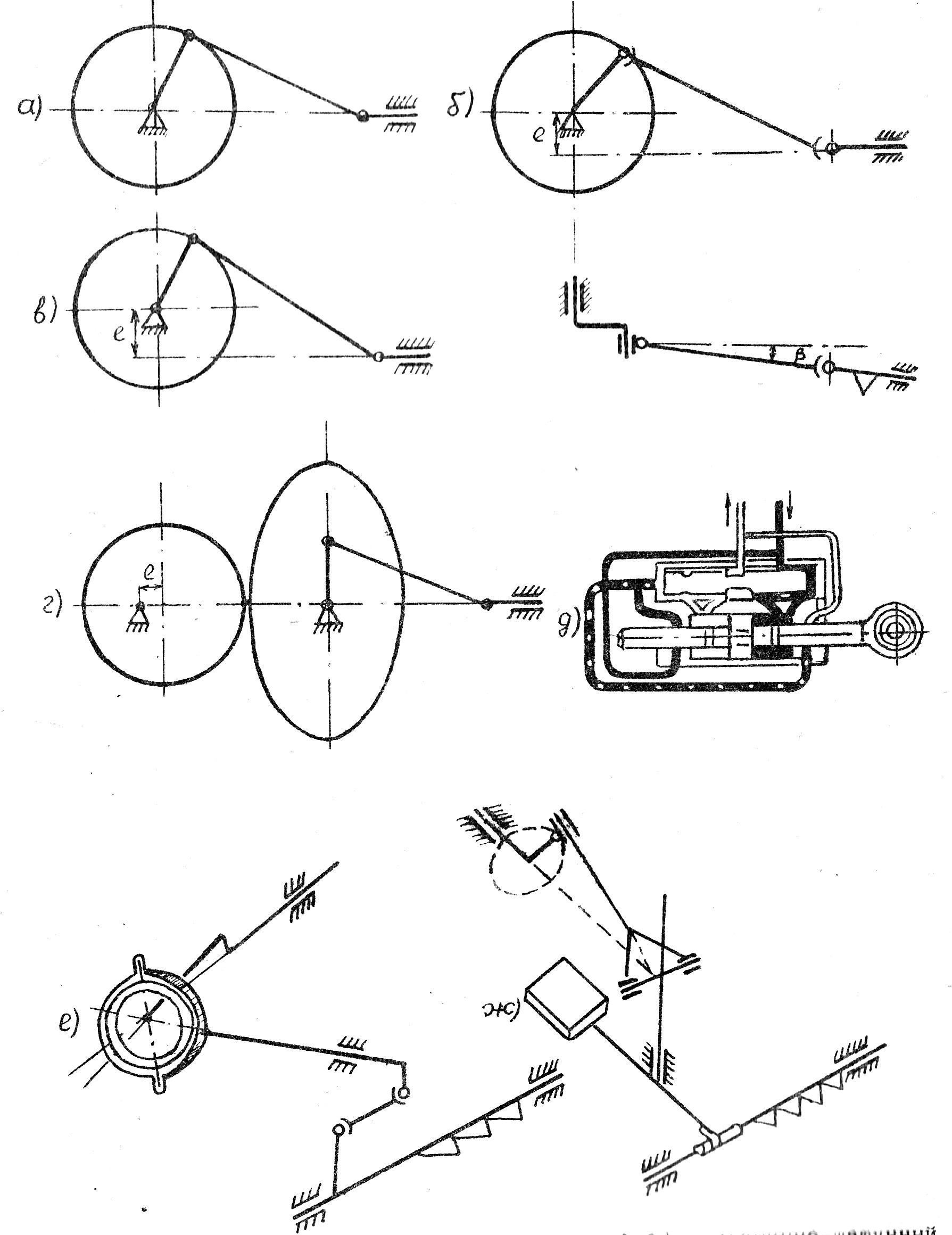
Рис. 2. Механизмы привода ножа: а ‑ кривошипно-шатунный аксиальный плоский; б ‑ кривошипно-шатунный дезаксиальный пространственный; в ‑ кривошипно-шатунный дезаксиальный плоский; г ‑ с некруглыми зубчатыми колесами; д ‑ гидравлический; е ‑ качающаяся шайба; ж ‑ качающаяся вилка

При малом значении отношения радиуса кривошипа r к длине шатуна l движение ножа может быть описано уравнениями гармонического колебания:

;

;

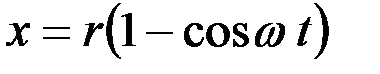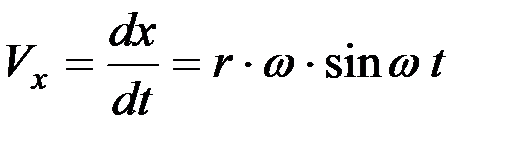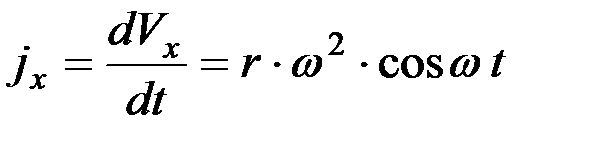. (2)

Максимальное значение скорости ножа соответствует окружной скорости кривошипа:

,

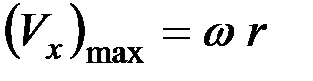а ускорение

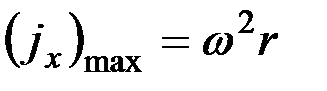
Рис. 3. Кинематические характеристики ножа

Как уже было отмечено, скорость ножа имеет большое технологическое значение. Если скорость ножа мала, срез затруднен, а растения затягиваются в зазор между сегментом и вкладышем пальца. Это явление может иметь место в момент разгона и остановки ножа в каждом цикле колебания. Чтобы устранить этот недостаток, пальцы у большей части аппаратов располагают достаточно редко, чтобы нож к моменту начала резания уже прошел определенный путь x_i (рис. 4) и успел разогнаться до необходимой скорости.

Для определения скорости начала и конца резания у пальцев режущего аппарата уравнение (2) лучше представить в функции от перемещения ножа х, а не угла поворота кривошипа w • t.

Из первого уравнения можно найти величину

.

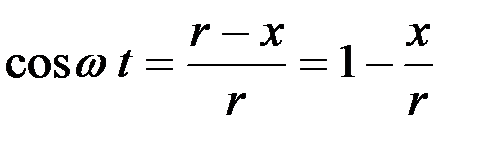Рис. 4. График скоростей ножа в зависимости от перемещения

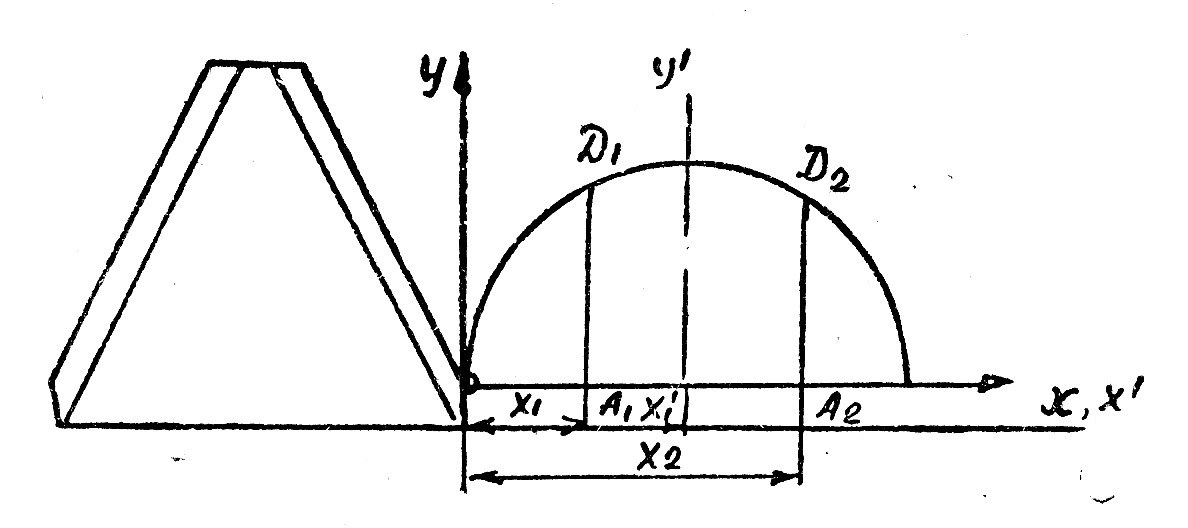
По величине cos wt легко определится синус этого угла:

.

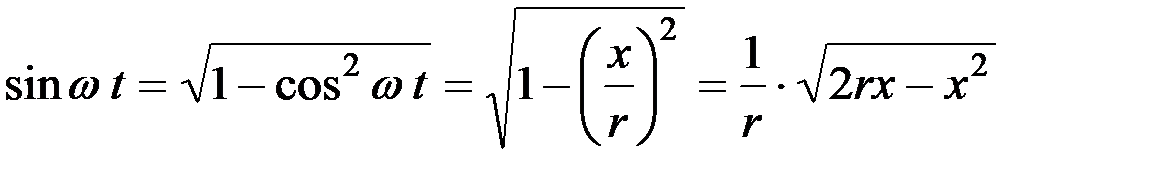Подставляя sin wt в выражение для V_x, можно получить

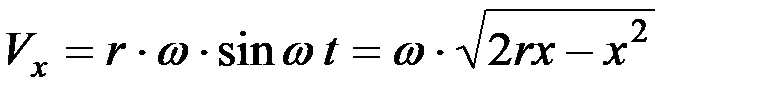. (3)

Аналогично находят и уравнение для определения ускорения:

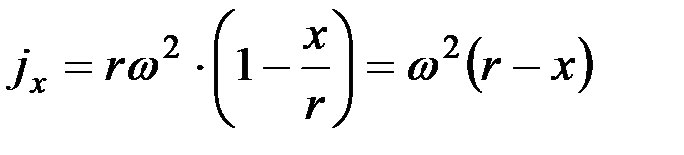. (4)

Графически зависимости (3) и (4) представлены на рис. 3, причем ускорение меняется в этих координатах по линейной зависимости, а скорость ‑ в определенном масштабе по дуге окружности.

В самом деле, если рассмотреть величину

у = V_x/w

(часто говорят, что это скорость ножа в масштабе w), то

;

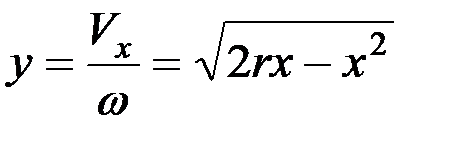у² = 2rх‑ х²;

х² + у² = 2rх.

Если центр координат графика y¢ = V_x/w перенести на расстояние r вправо от исходного положения ножа (точки А₀), т. е.

х' = r ‑ х,

то

(r - х')² + (у¢)² = 2r(r - х');

r² – 2rх' + (х')² + (у¢)² = 2r² – 2rх'; (х')² + (у¢)² = r²;

иначе говоря, в новой системе координат получена окружность радиусом r.

Построение такой окружности используют при графическом определении скорости ножа при любом перемещении, заданном величиной х или х' (рис. 4).

Таким образом, скорость ножа в период резания является величиной переменной, изменяющейся в довольно широких пределах. Так как в основном стебли перерезаются сегментом у кромки пальцев, то скорость резания будет зависеть от шага размещения сегментов и пальцев, т. е. от типа анализируемого режущего аппарата.

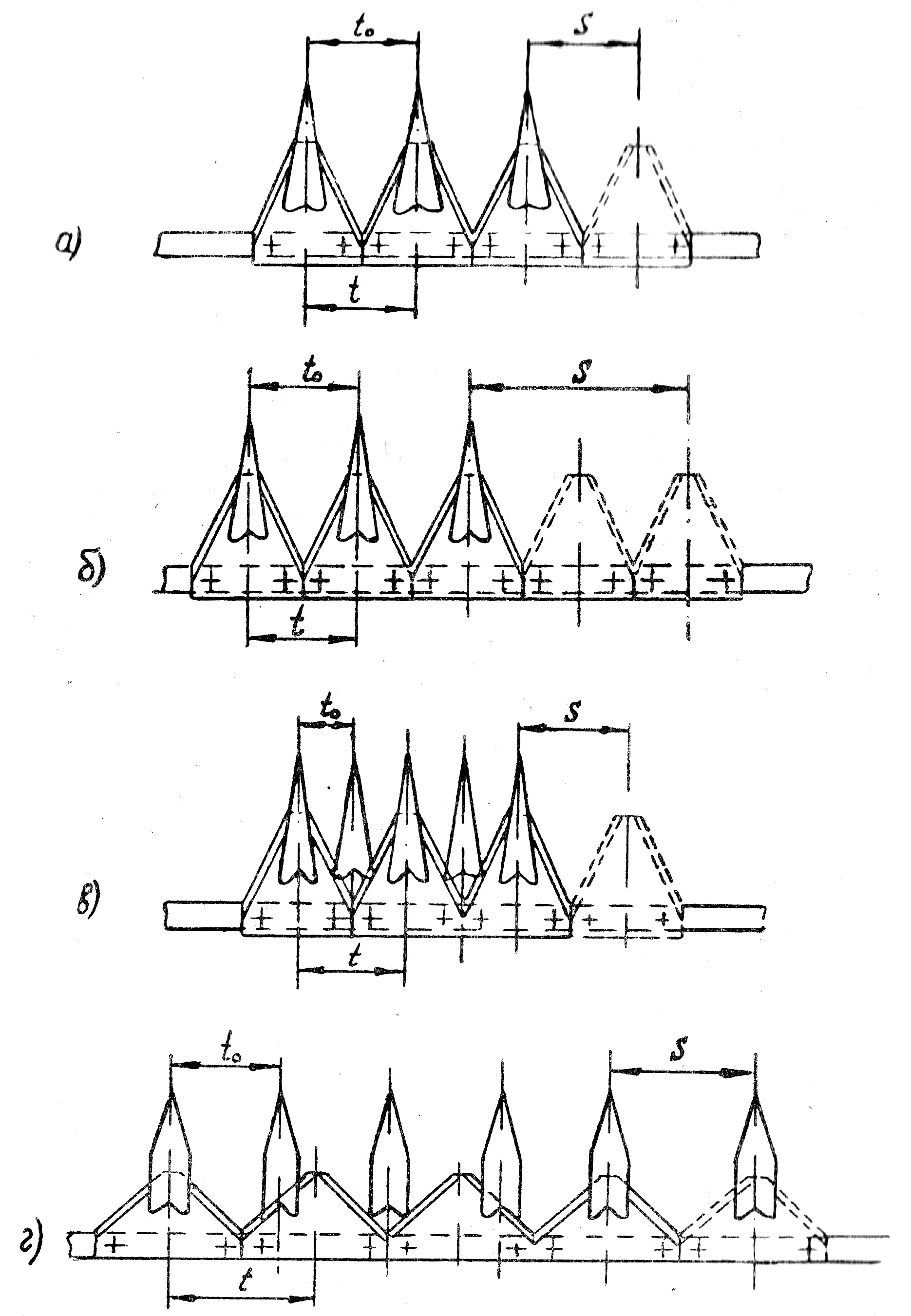
Известно, что в зависимости от соотношения шага режущей и противорежущей частей аппараты подразделяют на несколько типов (рис. 5). Прежде всего это аппараты нормального резания: однопробежные, где t = t₀ = S (рис. 5а), двухпробежные, у которых S = 2t = 2t₀, низкого резания, когда S = t = 2t₀, и среднего резания, при S = t = 4t₀/3.

У аппарата нормального резания (однопробежного) скорость начала резания определится величиной хода ножа х_н (рис. 6), когда нижняя рабочая точка лезвия А (перемещающаяся перед упорным отростком пальца) коснется противорежущей пластины в точке А₁ На рис. 6а видно, что

Рис. 5. Типы режущих аппаратов

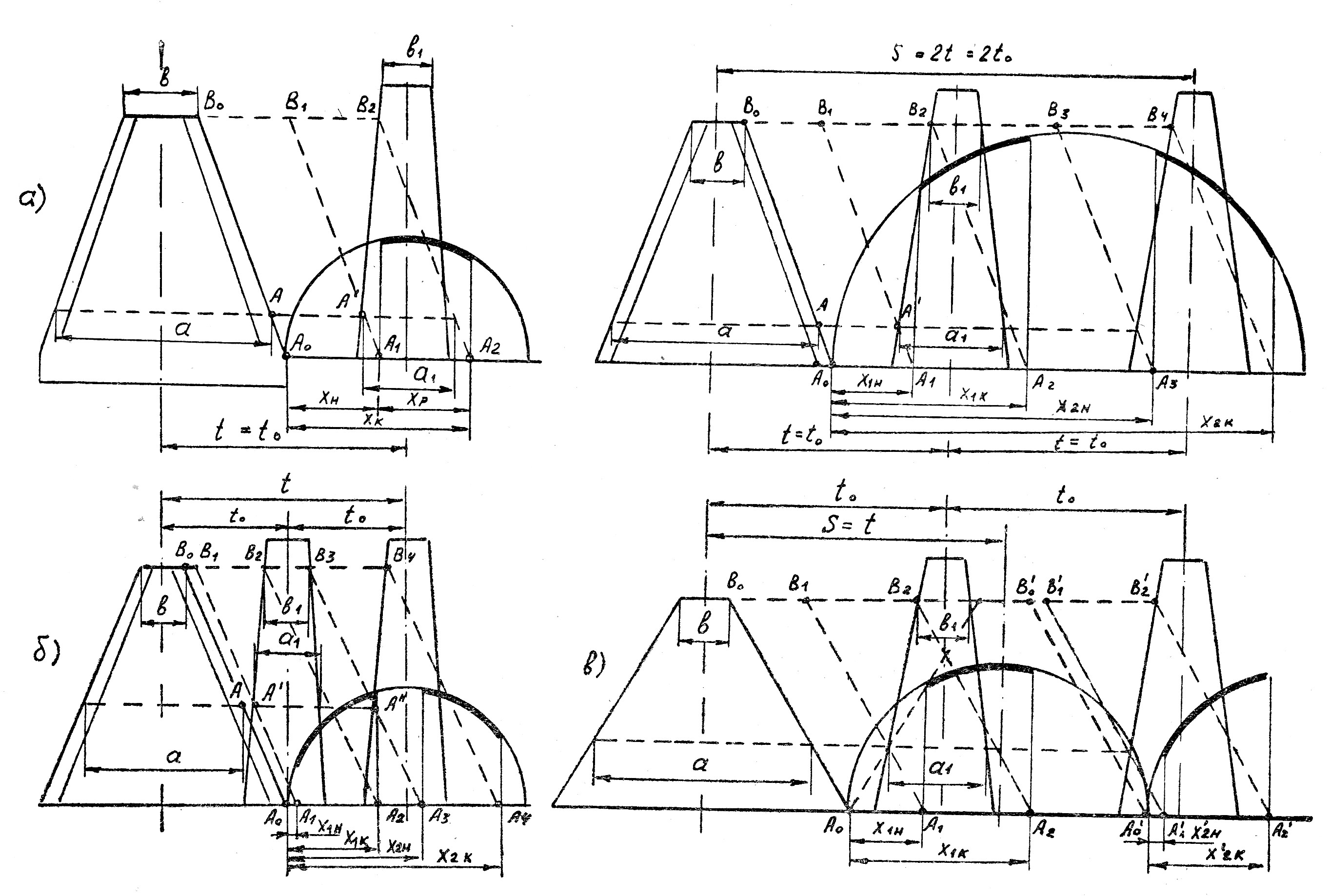
Рис. 6. Определение скоростей ножа в моменты начала и конца резания

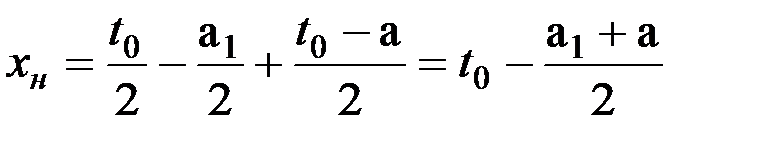. (5)

Конец резания наступит тогда, когда вершина лезвия (точка В₀) подойдет к кромке пальца и окажется в точке В₂:

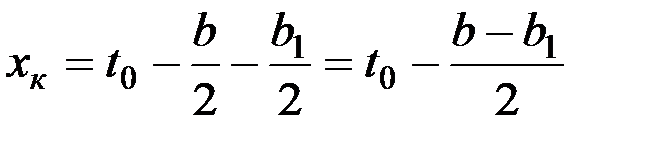. (6)

Для двухпробежного аппарата перемещение ножа в момент начала резания у среднего пальца х_1н равняется

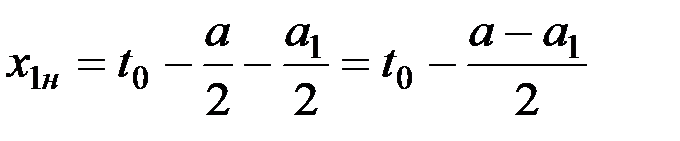. (7)

В момент начала резания у крайнего пальца это расстояние увеличится на шаг размещения пальцев, т. е.

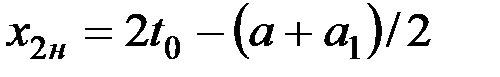. (8)

В момент конца резания у среднего пальца

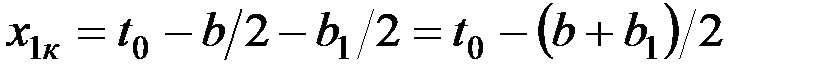, (9)

а у крайнего пальца

x _2к = 2 t ₀ - (b + b ₁)/2. (10)

У аппарата низкого резания (рис. 6б) в момент начала резания у среднего пальца, как в предыдущих случаях,

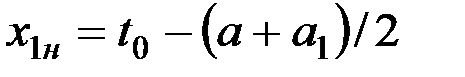, (11)

а у крайнего пальца

x _2н = t - (а + а ₁)/2. (12)

В момент конца резания у среднего пальца

x _lк = t ₀ - (b + b ₁)/2, (13)

а у крайнего пальца

x _2к = t - (b + b ₁)/2. (14)

Для аппаратов среднего резания характерными оказываются следующие соотношения:

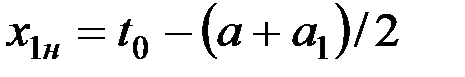; (15)

x _2н = 2 t ₀ – t – (а + а ₁)/2; (16)

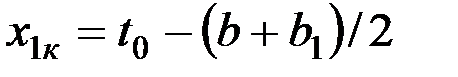; (17)

x _2к = 2 t ₀ – t – (b + b ₁)/2. (18)

Подставляя найденные значения х_н и х_к в уравнение (3), можно найти величину скорости начала и конца резания растений аппаратами различных типов.

В контрольном примере произведен расчет скорости начала и конца резания для всех типов режущих аппаратов с возвратно- поступательным движением ножа. Исходные данные учитывают особенности размеров каждого типа аппарата.

Анализ результатов показывает, что у режущих аппаратов, с приводом от кривошипно-шатунного механизма наблюдается значительная разница между скоростью V_max в середине хода и в граничных точках участка резания. Поэтому требуемую для резания скорость (2,8....3 м/с) не всегда удается обеспечить на протяжении всего процесса резания.

В то же время стремление обеспечить требуемую технологией резания скорость ножа в период среза всех растений приводит к завышению ее в середине хода и особенно к росту ускорений и связанных с ними сил инерции. Изыскание оптимальных кинематических диаграмм скорости и ускорения ножа, соответствующих одному его ходу, сводится к нахождению функции скорости с максимальным значением на участке резания и минимального значения функции ускорения на всем участке движения. Такая задача вариационного типа была решена следующим образом: рациональный привод ножа должен обеспечить кинематический режим, при котором график изменения скорости лезвия имеет вид равнобедренной трапеции (скорость ножа на всем участке резания остается постоянной, а ускорение минимально).

На рис. 7 построены оптимальные кинематические диаграммы перемещений x = f(wt), скоростей V = f(wt) и ускорений

j = f(wt), соответствующие одному обороту ведущего звена.

Наряду с кривошипно-шатуппым механизмом (см. рис. 2), для привода режущего аппарата применяются механизмы качающейся шайбы, качающейся вилки, некруглые зубчатые колеса и т. д. Анализ кинематических характеристик этих механизмов можно провести в сравнении с рассмотренным уже кривошипно-шатунным с точки зрения степени приближения их к оптимальному виду (программа «Резание» (Rezanie)).

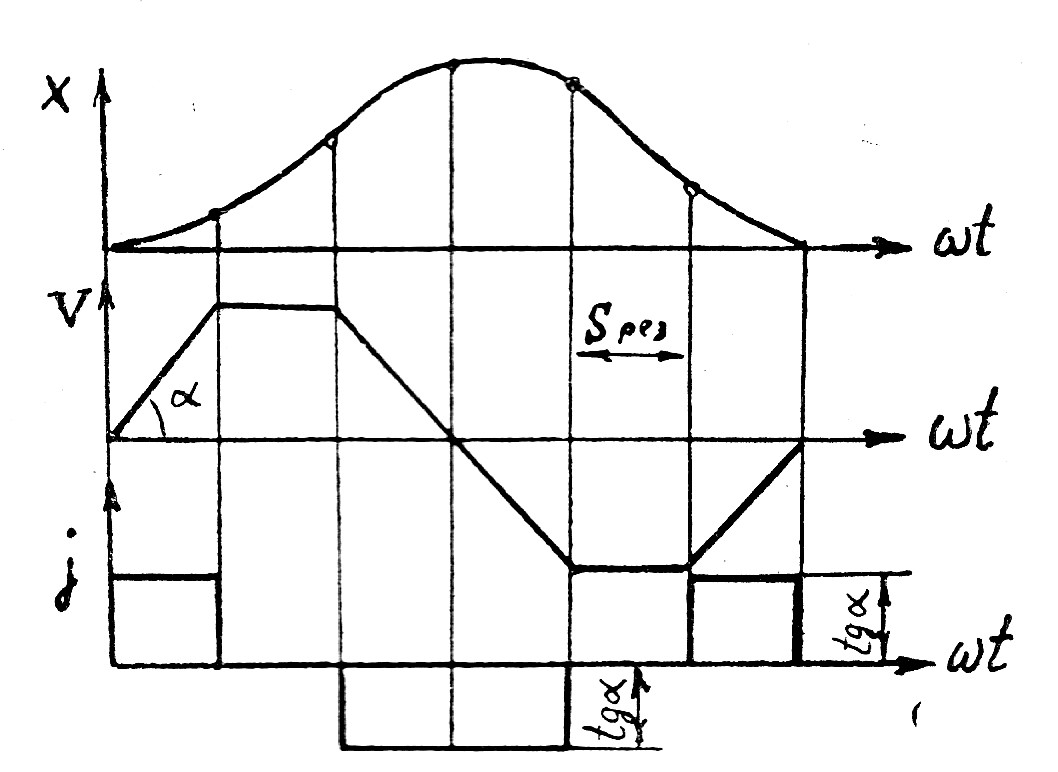
Рис. 7. Оптимальные кинематические диаграммы ножа

2.3. Диаграмма движения сегмента

Сегмент режущего аппарата участвует в сложном движении. Оно складывается из относительного движения (уравнение 2.22) и переносного вместе с машиной со скоростью V_M, определяемого уравнением

у = V_м × t. (19)

Путь, проходимый за один ход ножа или за половину оборота кривошипа, называется подачей и определяется, как

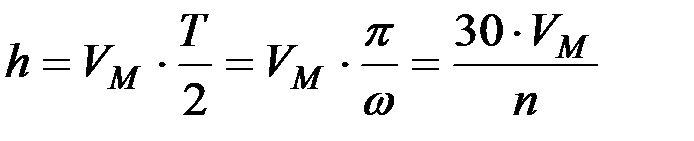, (20)

где Т ‑ период колебания ножа; п ‑ частота колебаний.

Из уравнения (2.62) можно получить

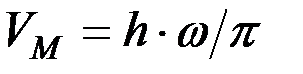. (21)

Подача h может явиться и характеристикой w, а еще точнее - отношения w/V_M:

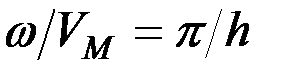. (22)

Из уравнения переносного движения (19) получают

t = у /V_м.

Подставляя t в уравнение относительного движения ножа (22), находят закономерность движения сегмента:

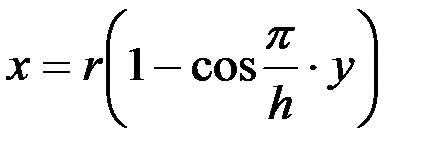. (23)

Следовательно, траектория любой точки ножа представляет собой косинусоиду.

Если из характерных точек (вершины и основания) сегмента провести косинусоиды при прямом и обратном ходе ножа, то поверхность поля покроется площадками, по которым пробегают рабочие лезвия ножей. В сочетании с траекториями движения пальцев (а это ‑ прямые линии, отстоящие от оси пальцев на расстоянии b и параллельные оси у) эти площадки представляют собой диаграмму движения сегмента (рис. 8).

Как видно из рис. 8, не вся поверхность поля пробегается лезвиями ножа. Незаштрихованный участок от точки Е до F не попадает в зону траекторий точек лезвия. Стебли, расположенные на этой площадке, будут отогнуты вперед противорежущим брусом и окажутся срезанными в точке F при обратном движении сегмента. Иначе говоря, стебли на участке от точки Е до F будут срезаны после продольного отгиба. Максимальная величина отгиба q_прод равна отрезку EF. Если учесть, что нож расположен на высоте Н от поверхности поля, то высота стерни L_прод может быть определена по теореме Пифагора:

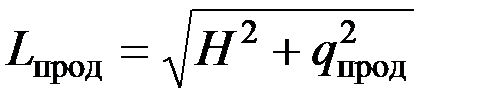. (24)

На заштрихованном участке траектории лезвия стебли будут наклонены движущимся сегментом в сторону и окажутся перерезанными у противорежущей кромки ближайшего пальца. Этот отгиб называют поперечным. Максимальная величина поперечного отгиба может быть представлена в виде отрезка MN, если стебель, находящийся в точке М, пальцем будет отклонен влево по ходу движения машины. Если учесть, что стебель обладает некоторыми упругими свойствами, то можно предположить возможность его скольжения относительно лезвия. В этом случае отгиб стебля произойдет под минимально возможным углом Q_min к оси х.

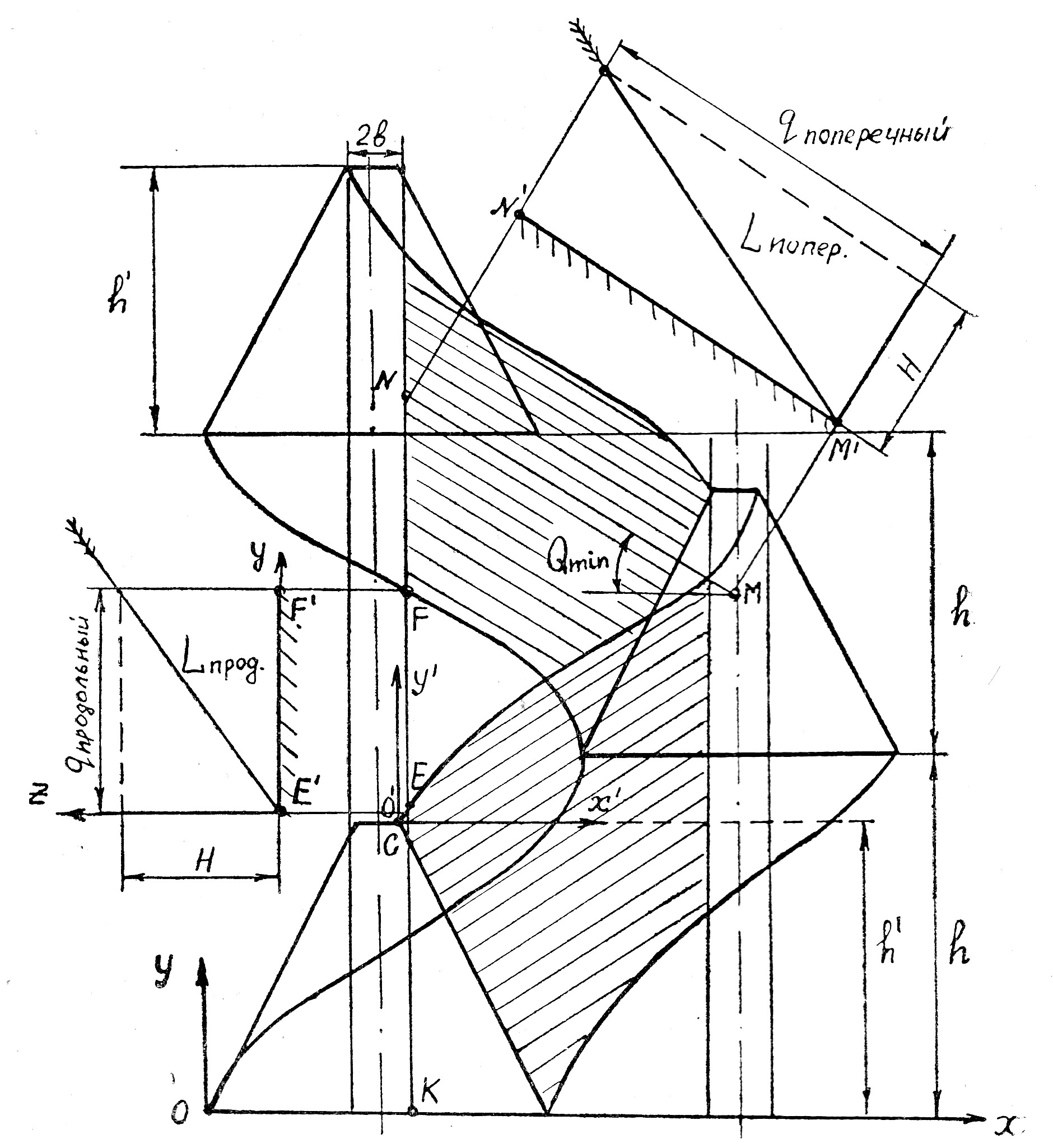
Рис. 8. Диаграмма движения сегмента

Поскольку движение сегмента может быть описано, как

,

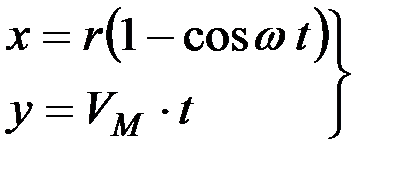то угол наклона касательной к траектории по отношению к оси х окажется равном

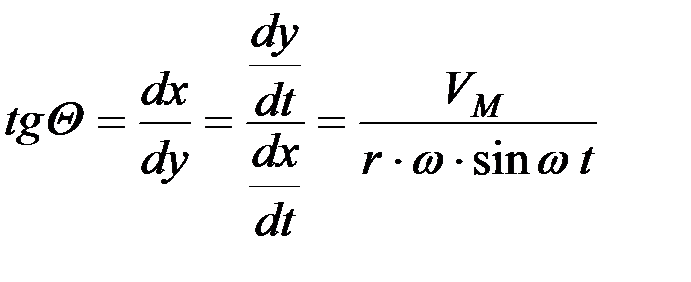
Наименьшее значение угла Q_min окажется при wt = p/2, значит, tg Q_min = V_M/(rw).

Если учесть, что по уравнению (22)

,

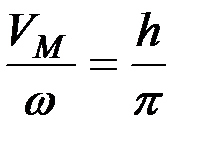то

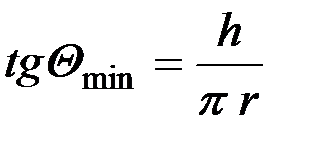(25)

После определения Q_min нахождение длины отрезка MN и L_попер не составляет труда,

.

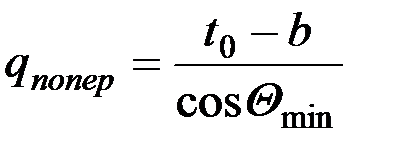В свою очередь,

.

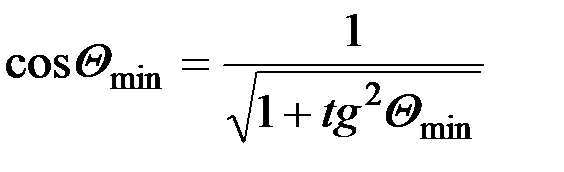Тогда

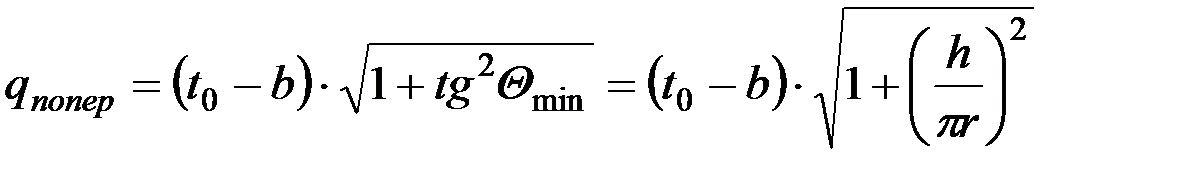. (26)

Высота стерни после поперечного отгиба будет равна

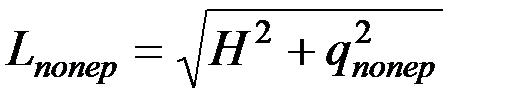. (27)

Величина продольного отгиба может быть определена аналитически:

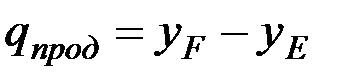. (28)

По уравнению (23),отнесенному к осям х и у,

.

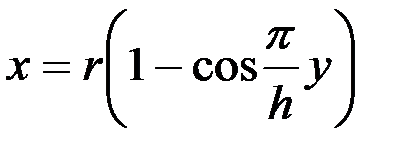Прямая KN, проведенная параллельно оси у на расстоянии

х₁ = r+b,

пересечет косинусоиду в нескольких точках, в том числе и в точке F:

,

.

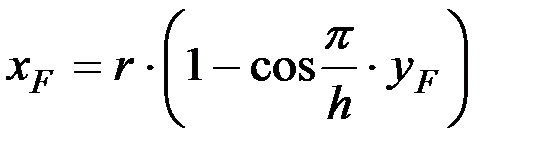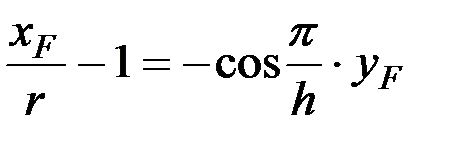Срез растений в точке F произойдет, когда вал кривошипа повернется на угол

p < wt < 1.5p,

т. е. wt будет в третьей четверти угла поворота. Из тригонометрии известно, что в третьей четверти для любого произвольного угла a

.

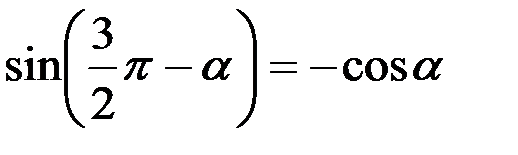Для рассматриваемого случая это будет означать

,

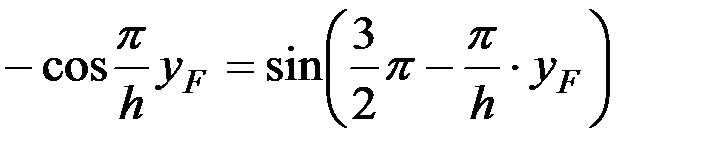тогда

.

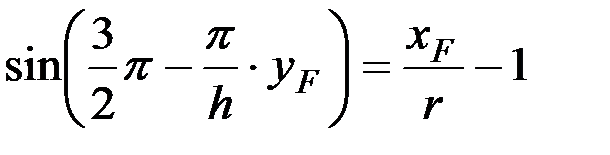Учитывая, что x_F = x ₁ = r + b, можно получить

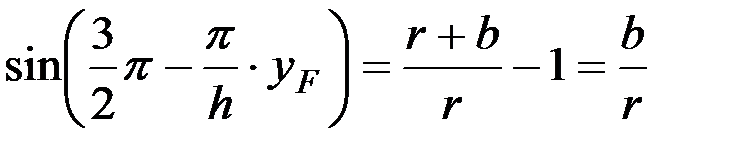
Отсюда

,

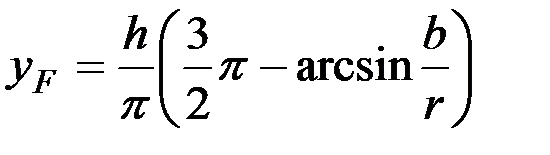т. е.

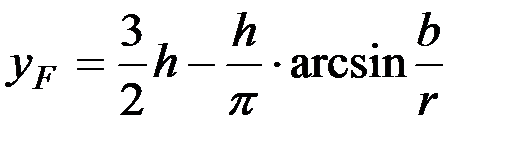. (29)

Чтобы определить координату у_Е точки Е, необходимо заметить, что ветвь косинусоиды СЕ является такой же, что и косинусоиды, выходящей из начала координат О, но сдвинутой вверх на высоту сегмента h' и вправо на r+b', где b' ‑ половина верхнего основания сегмента. Если за начало этой косинусоиды принять точку О', то косинусоида СЕ будет записана в той же форме, что и выходящая из точки О, т. е.

.

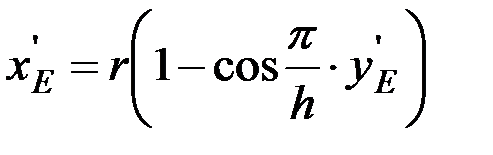Координата у¢_Е, очевидно, найдется для того значения х¢_Е, которое соответствует удалению кромки KN пальца от оси о'у:

,

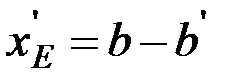тогда

,

,

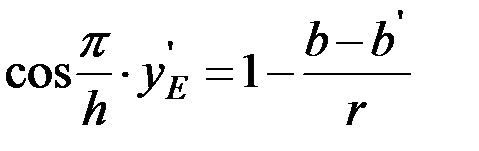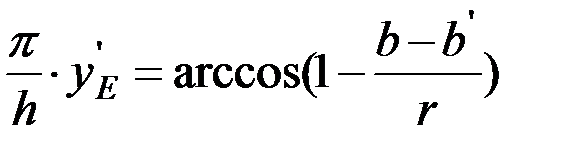
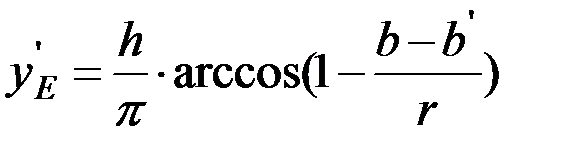
Учитывая, что

y_E = y_E + h^/,

можно найти

,

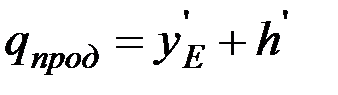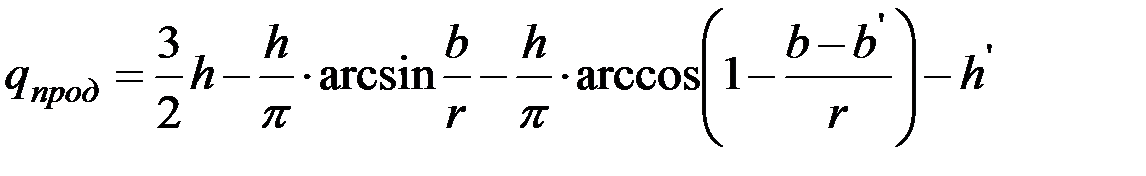
или

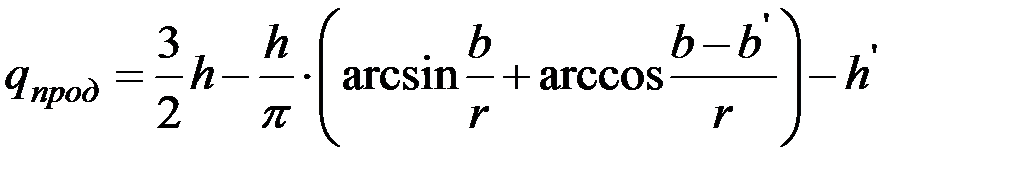. (30)

Высота стерни после продольного отгиба определяется так:

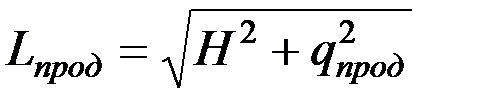. (31)

Дата добавления: 2015-06-04