
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Динамическое уравнение барабана и его анализ
|
|
|
|
Первым аналитическим описанием системы двигатель – барабан – растительная масса явилось уравнение барабана академика В. П. Горячкина.
Мощность двигателя, подведенная к молотильному аппарату, расходуется на преодоление сопротивления холостого хода и обмолот хлебной массы:
N oбщ = N xx + N oбм.
Мощность Nхх зависит от частоты вращения барабана:
N xx = A×w + B × w3, (7)
где А × w — слагаемое, учитывающее сопротивление подшипников барабана;
В × w3 — слагаемое, отражающее сопротивление воздуха;
w — частота вращения барабана;
А, В — коэффициенты, определяемые опытным путем, имеют следующие значения: для бильного барабана А = 0,3...0,4 Н×м и В = (0,8...0,9) 10-3 Н×м×с2; для зубового барабана А = 3...4 Н×м и В = (0,5...0,6) 10-3 Н×м×с2.
Мощность, необходимая для обмолота, определяется с помощью основного уравнения удара, при этом допускается, что в результате неупругого удара хлебная масса, поступающая в барабан, приобретает скорость, равную окружной скорости бичей. Удары сообщаются непрерывно поступающим массам Dm, которые приобретают скорость V за время удара Dt.
Согласно основному уравнению удара, известному в механике, импульс силы равен приращению количества движения:
P1×Dt = Dm×V. (8)
Усилие на планках барабана, преодолевающее силы инерции хлебной массы,
Р1 = Dm × V/Dt = m' × V,
где m' – величина секундной подачи хлебной массы.
Молотильный аппарат преодолевает еще сопротивление деки, которое пропорционально общему окружному усилию (так как удар бича о солому передается на деку и вызывает дополнительное трение соломы о ее решетку), т. е.
P2 = f × P,
где f – коэффициент сопротивления деки.
По данным исследований, f для барабанов бильного типа равен 0,65...0,75, а для зубовых – 0,7...0,8.
Полное усилие на поперечной планке барабана будет следующим:
P = P1 + P2 = m'V + fP,
откуда
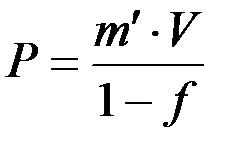 .
.
Умножая обе части этого уравнения на V, можно получить
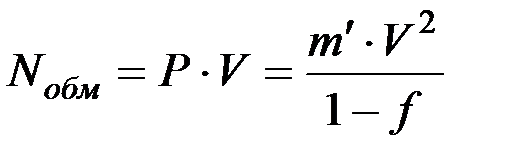 . (9)
. (9)
Энергия, подведенная от двигателя, обеспечивает разгон молотильного аппарата:
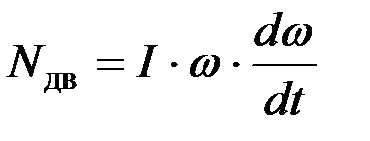 , (10)
, (10)
где I – момент инерции барабана;
w – угловая частота барабана;
dw/dt – угловое ускорение.
Запас мощности вращающегося барабана, описываемый уравнением (10), по мнению В. П. Горячкина, должен быть равным мощности, необходимой для обмолота (9), т. е.
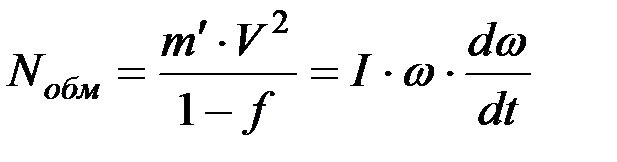 . (11)
. (11)
Это положение можно объяснить ударным характером воздействий барабана на хлебную массу. Силы, возникающие при ударе, очень велики, и если запас мощности невелик (например, величина момента инерции барабана мала), то возможна пробуксовка шкива относительно приводного ремня. Если запас мощности вращающегося барабана достаточен, то за счет этого будет обеспечено ударное воздействие бичей на хлебную массу, а восполнение потерь мощности будет происходить от двигателя в промежутках времени между ударами, которые значительно превосходят время удара t. Скольжение приводного ремня относительно шкива будет у такого барабана меньше
Соотношение (11) получило название основного уравнения молотильного барабана.
3.3. Скорость хлебной массы в подбарабанье
Время нахождения обмолачиваемой массы между декой и барабаном, а следовательно, и число ударов, наносимых бичами по колосьям, зависит от скорости движения растений в молотильном зазоре.
Наблюдения за работой молотильного аппарата показали, что барабан, перемещая растительную массу, имеет большую, чем ворох, скорость, а это приводит к проскальзыванию барабана относительно потока вороха.
Если выбрать на барабане фиксированный радиус, проходящий через входную планку деки, то за время t он повернется на угол y. За это же время поступившая в подбарабанье порция растительной массы повернется на угол j относительно оси барабана, при этом j < y и 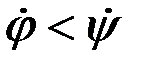 .
.
Для определения скорости 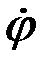 необходимо прежде всего установить взаимосвязь между скоростями
необходимо прежде всего установить взаимосвязь между скоростями 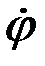 растительной массы и
растительной массы и  барабана, а также определить функцию j = j(t), т. е. характер изменения скорости порции во времени или по углу охвата.
барабана, а также определить функцию j = j(t), т. е. характер изменения скорости порции во времени или по углу охвата.
Пусть углы поворота барабана y и хлебной массы j будут использованы в качестве обобщенных координат системы барабан – хлебная масса.
С известным приближением можно полагать, что средние скорости барабана и порции вороха за время t могут быть выражены полусуммами величин скоростей на границах интервала, тогда
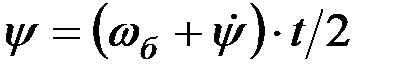 ; (12)
; (12)
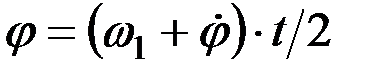 ; (13)
; (13)
где wб – угловая частота барабана на холостом ходу;
w1 – угловая частота порции хлебной массы в подбарабанье;
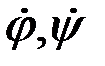 – текущие угловые скорости барабана и порции растений.
– текущие угловые скорости барабана и порции растений.
Одним из наиболее общих способов описания динамики системы механических элементов является составление уравнения Аппеля:
 ,
,
где S – энергия ускорений;
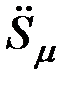 – независимая обобщенная координата;
– независимая обобщенная координата;
Qm – обобщенная сила, соответствующая независимой обобщенной координате.
Применительно к движению барабана и хлебной массы в молотильном зазоре энергия ускорений может быть представлена уравнением
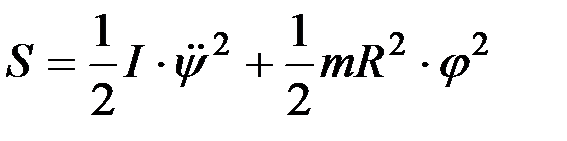 , (14)
, (14)
где I – момент инерции барабана;
m – масса порции вороха.
Частная производная энергии ускорений по независимой обобщенной координате будет равна:
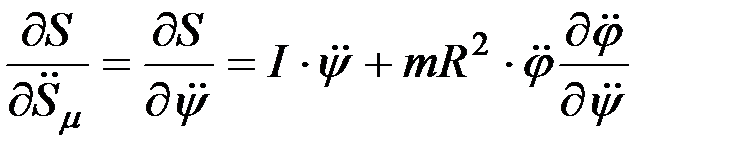 . (15)
. (15)
Расчеты величины скорости хлебной массы в молотильном зазоре для барабана длиной 1,2 м при изменении подачи от 4 до 8 кг/с приведены в табл.[1].
Таблица 1 Зависимость скорости вороха на выходе из массы молотильного зазора от величины подачи хлебной массы
| q. | Nсp, | Н, | w, | V, |
| кг/с | кг | 1/с2 | 1/с | м/с |
| 4,0 | 21,5 | 210,8 | 39,7 | 10,9 |
| 4,3 | 28,0 | 255,9 | 41,7 | 1 1,5 |
| 5,0 | 48,4 | 380,0 | 47,7 | 13,1 |
| 5,3 | 58,5 | 436,0 | 49,9 | 13,7 |
| 5,6 | 68,8 | 483,0 | 51,3 | 14,1 |
| 6,5 | 86,5 | 523,4 | 53,7 | 14,8 |
| 8,0 | 93„2 | 483,0 | 51,3 | 14,1 |
3.3. Модель процессов обмолота и сепарации зерна через решетку подбарабанья
Пусть перемещение потока растительной массы происходит при средней толщине и скорости.
Процесс обмолота и сепарации обычно считают однородным по времени.
Пусть х – число необмолоченных зерен в подбарабанье;
у – количество обмолоченных свободных зерен в подбарабанье;
z – число зерен, прошедших сквозь решетку деки.
Для любого отрезка времени движения хлебной массы справедливо соотношение
X = x + y + z = const, (16)
где X – количество зерна, поступившего в молотильный аппарат.
При обмолоте число необмолоченных зерен убывает. Скорость убывания можно представить как функцию, зависящую от числа необмолоченных зерен
 , (17)
, (17)
где b – коэффициент пропорциональности (величина постоянная), 1/с.
Аналогично можно определить скорость сепарации зерна:
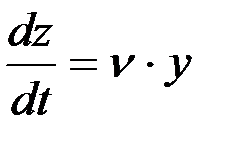 , (18)
, (18)
где n – коэффициент пропорциональности (величина постоянная), 1 /с.
Скорость изменения числа свободных зерен, остающихся в подбарабанье, можно представить в виде разности
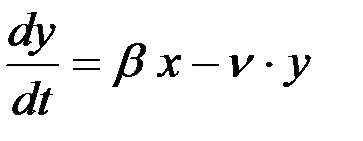 . (19)
. (19)
Значение bх в данном случае записано со знаком + (плюс), так как выражает скорость возрастания числа свободных зерен.
Изменение общего числа зерен X выразится системой дифференциальных уравнений:
 . (20)
. (20)
Если эти уравнения проинтегрировать (подобное решение приводится в учебном пособии [2]), то модель обмолота и сепарации зерна может быть представлена кривыми рис. 4.
Кривая уравнения Y(t) проходит через начало координат (рис. 4). Этот случай получен из предположения, что в начальный момент времени (t = 0) количество свободных зерен равно нулю. Но при этом упускают из виду то обстоятельство, что обмолачивающим свойством обладают и другие рабочие органы комбайна (транспортеры, битеры), а кроме того, первый удар бича по колосу наносится до входа хлебной массы в молотильный зазор. Далее следует отметить, что первая стадия обмолота проходит до входа в молотильный зазор, хотя первая поперечная планка деки уже участвует в технологическом процессе, воспринимая удар бича, передаваемый через слой зажатой хлебной массы. В результате такого воздействия из колоса выделяются 30…60% зерен (в зависимости от вида культуры и сроков уборки).
В модели, на которой построена компьютерная программа «Obmolot» это обстоятельство учтено, и графики x(t), y(t), z(t)принимают несколько иной вид

| Рис. 4. Графики функций, отражающие количество необмолоченных и обмолоченных зерен, а также семян, просеявшихся через решетку подбарабанья |
Более полное изложение теории обмолота хлебной массы содержится в [1], [2], [3].
Обоснование основных параметров молотильного барабана (пример)
Пусть Qз = 25 ц/га; Qс = 40 ц/га; Vм = 5 км/ч; В = 6 м.
1. Подача хлебной массы в молотилку составит (1)
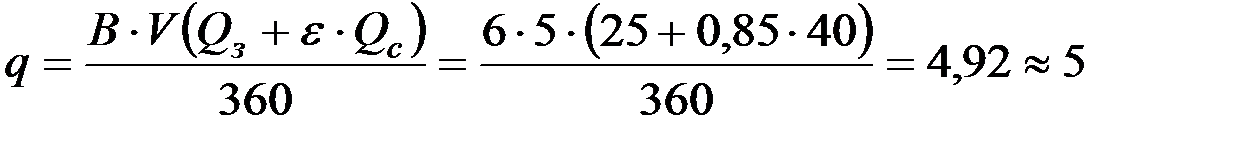 кг/с,
кг/с,
где e = 0,8…0,9 – коэффициент, учитывающий долю соломы, поступающей в комбайн.
2. Суммарную длину бичей определяют по допустимой нагрузке q0 на один метр бича, q0 = 0,5…0,35 кг/м×с.
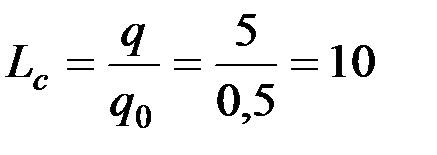 м.
м.
3. Находят длину барабана Lб, учитывая возможное число бичей z
 м,
м,
где число бичей z = 6…10.
4. Определяют диаметр барабана
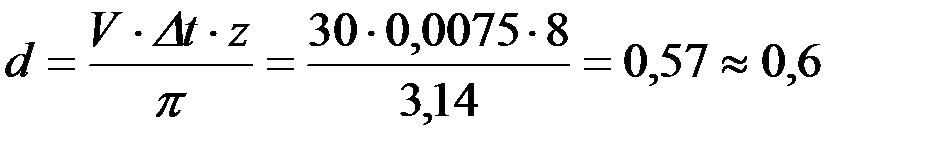 м,
м,
где Dt – оптимальное время соударения бичей с хлебной массой, при котором происходит интенсивный обмолот, Dt» 0,0075 с.
5. Мощность, затрачиваемая на обмолот
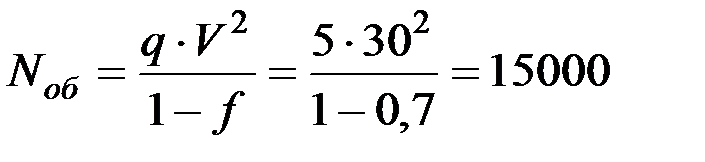 Вт,
Вт,
где V = 30 м/с – скорость бичей; f – коэффициент сопротивления деки.
6. Мощность, затрачиваемая на холостой ход
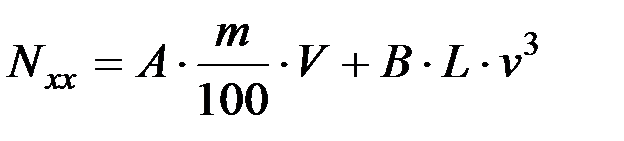 ,
,
где А = 0,85…0,9 Н на каждые 100 кг массы барабана; В = 0,065 Н×с2/м2 – на 1 метр барабана; m – масса барабана, кг.
7. Для определения массы барабана предварительно находят его момент инерции I по основному уравнению молотильного аппарата (11)
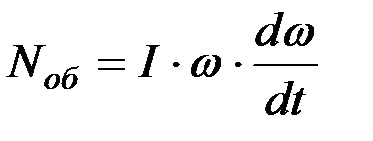 , откуда
, откуда  кг×м2,
кг×м2,
где 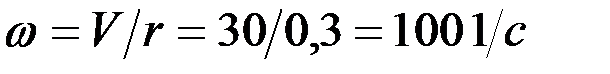 ,
, 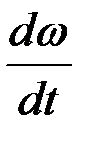 - допустимое ускорение барабана (12…15 1/с2).
- допустимое ускорение барабана (12…15 1/с2).
8. Поскольку 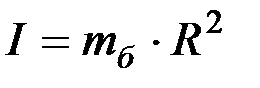 , то
, то 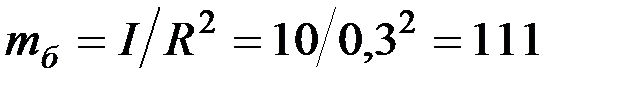 кг
кг
9. 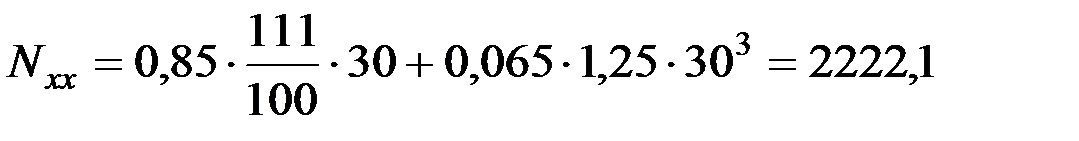 ватт.
ватт.
10. Общая мощность, необходимая для работы барабана составит
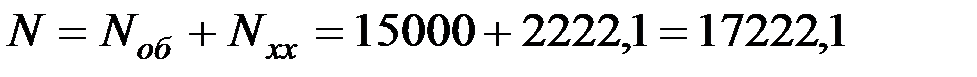 ватт
ватт
Примеры числового анализа модели обмолота, построенной на уравнении Аппеля с учетом перемещения переменной массы и регрессивных уравнений недомолота и дробления зерна можно получить с использованием программы «Obmolot».
Литература
1. Б.Г. Турбин и др. Сельскохозяйственные машины. Л.: Машиностроение, 1967, - 583 с.
2. А.Ф. Кошурников и др. Анализ технологических процессов, выполняемых сельскохозяйственными машинами, с использованием ЭВМ. Часть 2. Пермь, 1998, 370 с.
3. Кленин Н.И. и др. Сельскохозяйственные машины. М.: КолосС, 2008, - 816 с.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 2719; Нарушение авторских прав?; Мы поможем в написании вашей работы!