Кинематические характеристики клавишного соломотряса

Пусть рабочая поверхность клавиши параллельна центровой линии соломотряса и наклонена к горизонту под углом a. Каждая точка клавиши, как было уже отмечено ранее, совершает круговое движение. Если начало координат поместить в центр коленчатого вала, ось OY направить параллельно поверхности клавиши, а ось ОХ ‑ перпендикулярно к ней (рис. 3), то легко определить положение любой точки в произвольный момент времени.

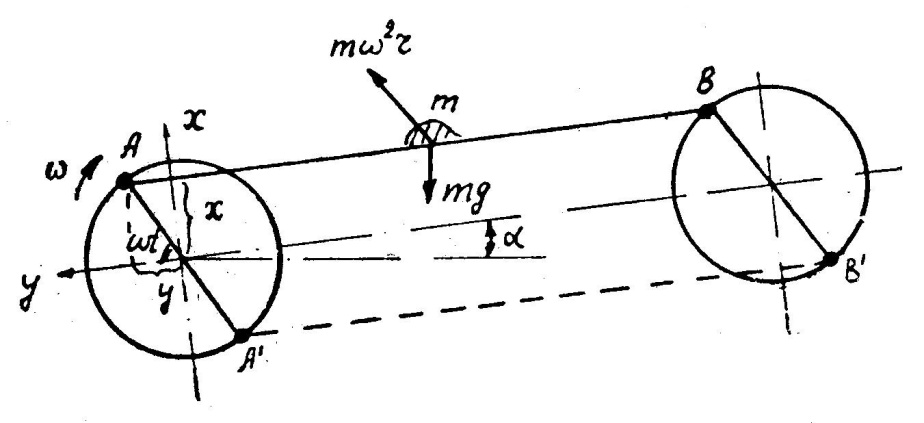
Рис. 3. Механизм двухвального клавишного соломотряса

Отсчет угла поворота коленчатого вала производится от оси OY в направлении его вращения. Если w ‑ угловая частота вращения вала, то угол wt определит положение клавиши, соответствующее некоторой точке А. Координаты этой точки, очевидно, будут следующие:

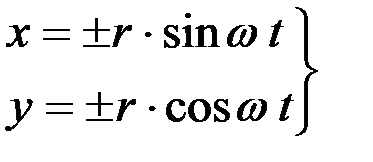; (1)

знаки «±» учитывают координаты точек А', В', в которых может оказаться вторая группа клавиш у пятиклавишного соломотряса.

Для определения скорости и ускорения клавиши необходимо продифференцировать уравнения (1):

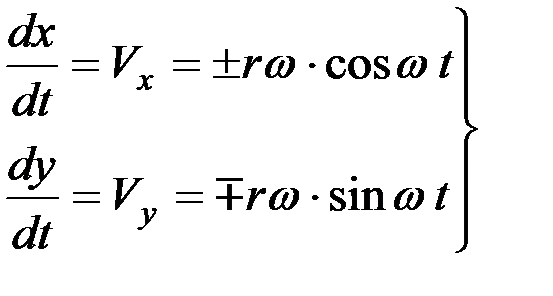. (2)

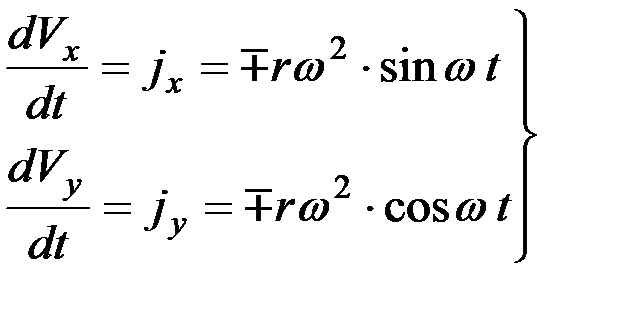. (3)

Хлебная масса m, лежащая на поверхности клавиши и участвующая вместе с поверхностью в круговом движении, будет находиться под действием центробежной силы mw²r и силы тяжести mg. От величины соотношения этих сил будет зависеть характер движения соломы. Если mw²r/mg будет меньше единицы, то масса не сможет оторваться от поверхности и будет двигаться лишь вместе с клавишей. При значении этого отношения, превышающем единицу, возможен отрыв массы от поверхности соломотряса. Вследствие этого данное отношение k считают основной кинематической характеристикой соломотряса:

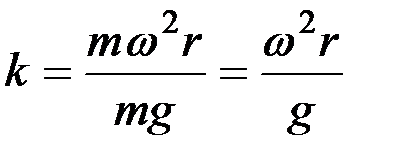, (4)

где k ‑ показатель кинематического режима соломотряса.

4.3. Основные уравнения соломотряса

Технологический процесс выделения зерна из соломы в значительной мере зависит от режима работы соломотряса. Легче зерно проходит сквозь слой соломы, если хлебная масса находится во вспушенном состоянии (например, в период свободного полета в воздухе). Но момент отрыва соломы от клавиши зависит от величины центробежной силы, а в конечном счете ‑ от k. Первое основное уравнение соломотряса определяет угол поворота коленчатого вала wt₁ (фаза отрыва), при котором произойдет отрыв хлебной массы от клавиши. Знание величины wt₁ позволяет определить направление начальной скорости соломы в свободном полете.

Второе уравнение соломотряса определяет угол wt₃ (фаза соударения), при котором произойдет соударение падающей соломы с поверхностью клавиши. От величины этой фазы будет зависеть сила соударения хлебной массы с клавишей (удар может быть слабым, попутным или сильным, встречным). Разумеется, от силы соударения также будет зависеть и эффективность сепарации зерна.

4.3.1. Первое основное уравнение соломотряса

Отрыв хлебной массы от поверхности клавиши произойдет в тот момент, когда величина нормального давления N на клавишу окажется равной нулю (рис. 4).

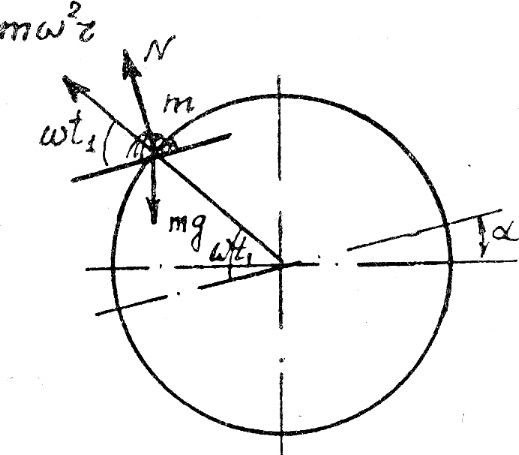
Рис. 4. Схема сил, действующих на хлебную массу в момент отрыва от клавиши

Итак, условием отрыва будет равенство N = 0.

Но

,

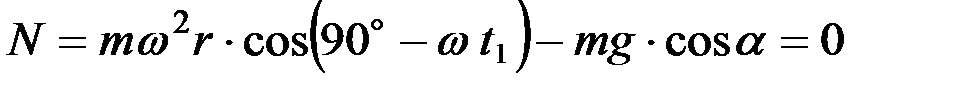тогда

,

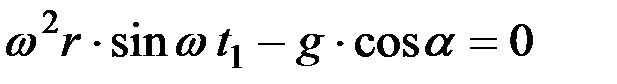или

,

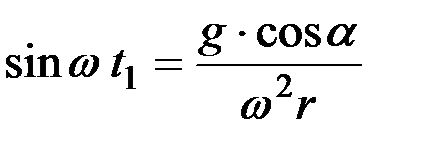. (5)

4.3.2. Второе основное уравнение соломотряса

Пусть в точке 1 (рис. 5) произойдет отрыв соломы от клавиши, и в дальнейшем движение хлебной массы можно рассматривать как полет тела, брошенного под углом к горизонту. Для описания траектории этого движения оси координат предпочтительней направить горизонтально и вертикально вверх.

Рис. 5. Схема перемещения соломы за одно подбрасывание

В свободном движении солома движется по параболе, поднимаясь до точки 2 на высоту D х ₂, после чего она падает вниз, пока снова не встретится с клавишами. Пусть эта встреча произойдет в точке а ₃, расположенной на D х ₃ ниже точки 2. В момент соударения точка 1, подбросившая солому, переместится в точку 3. В общем случае, разумеется, точка падения а ₃ не совпадет с точкой 3.

Если обозначить координаты точки 3 как х ₃, у ₃, а взаимное положение точек а ₃ и 3 охарактеризовать величинами D х _а, D у _а, то вертикальное и горизонтальное перемещения соломы могут быть описаны системой уравнений:

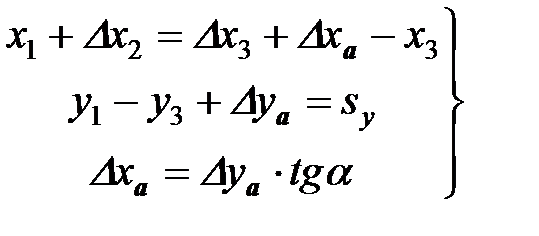. (6)

Иногда в литературе эти соотношения называют вторым основным уравнением соломотряса в отрезках [1]. При определении величин, входящих в равенство (6), встает вопрос о том, можно ли движение соломы описать без учета сопротивления воздуха. Большинство авторов рассматривают движение хлебной массы без учета сопротивления воздуха, ссылаясь, прежде всего на малую величину скорости соломы [1, 2]. Учет сопротивления воздуха к существенно новым выводам не привел.

Итак, в первом приближении отрезки, входящие в уравнение (6), могут быть определены без учета сопротивления воздуха.

Координата х ₁ определится так:

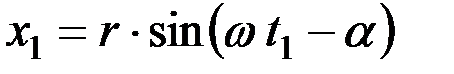. (7)

Высота подъема при отсутствии сопротивления воздуха равна:

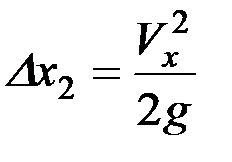, (8)

где V_x ‑вертикальная составляющая скорости соломы.

В свою очередь,

.

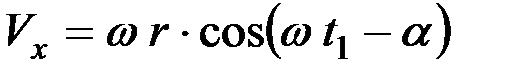Тогда

,

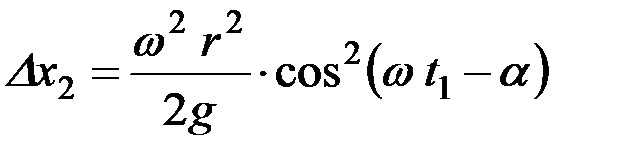или.

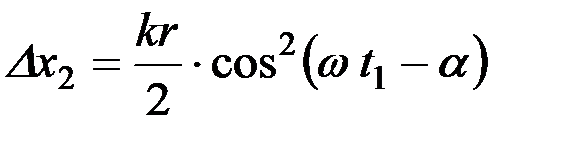. (9)

Координата x ₃ определится аналогично х ₁ но с учетом возможности падения соломы на ту или иную группу клавиш:

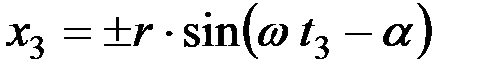. (10)

Высота свободного падения соломы

,

где Dt ₃ ‑ время падения.

Время падения соломы может быть определено по фазе отрыва wt₁ и соударения wt₃.

В самом деле,

Dt₃ = (wt₃ ‑ wt₂)/w,

где wt ₂‑ угол поворота коленчатого вала соломотряса в момент максимального подъема соломы.

Но

wt₂ = wt₁ + w Dt₂,

где Dt₂‑ время подъема соломы.

Поскольку высота подбрасывания уже найдена (9), то определение Dt₂ не составляет труда:

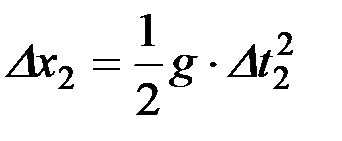
откуда

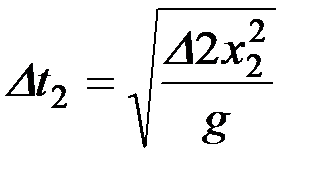
или

.

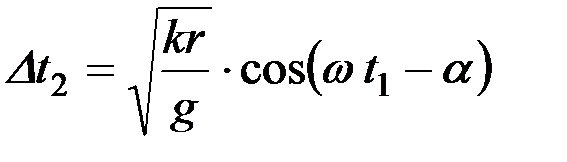Умножим правую и левую части уравнения на w:

.

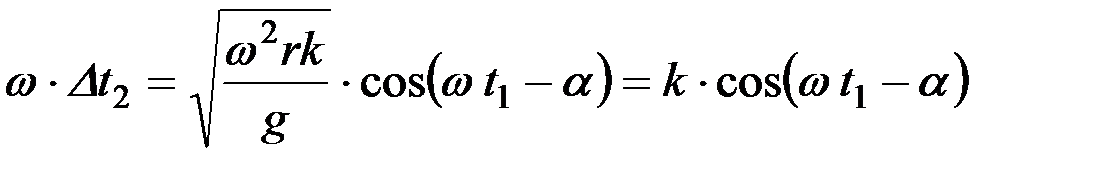В таком случае

.

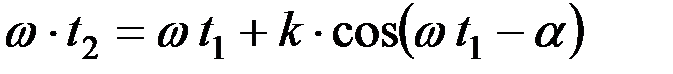Тогда

.

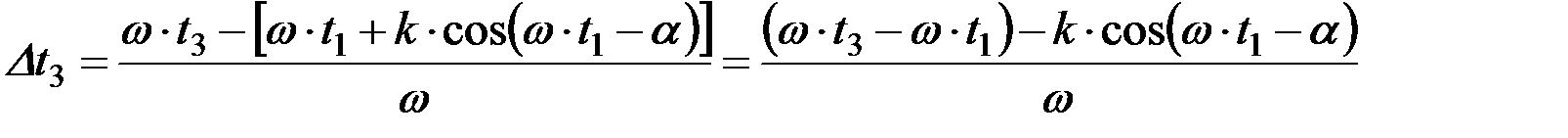Высота падения соломы теперь может быть определена так:

;

.

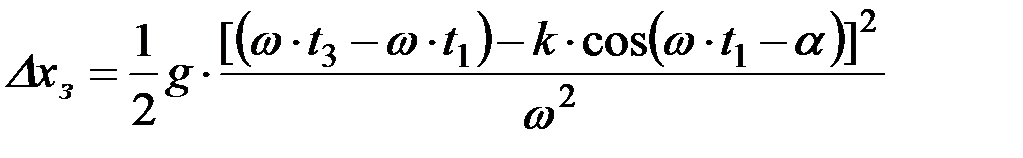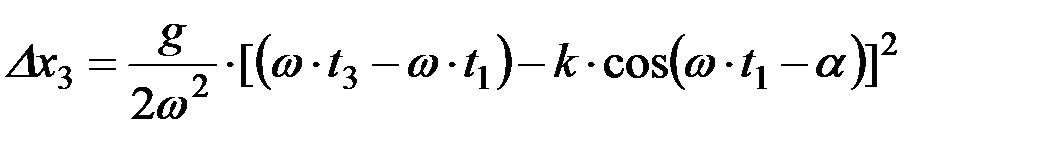Поскольку

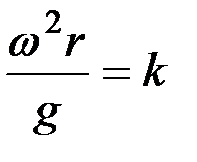, то ,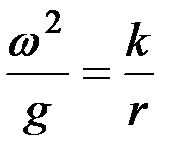

тогда

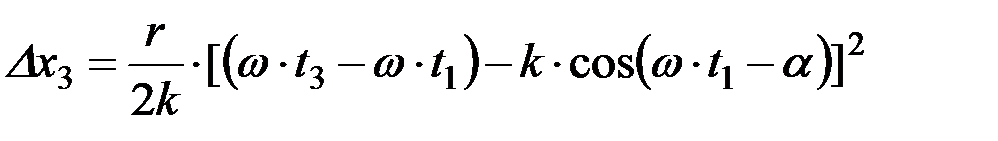. (11)

Отрезки Dх_а и Dу_а связаны соотношением

D x_a = D y_{a ×}tga.

Но

D y_a = y ₁ + у ₃ - S_y,

где S_y ‑ дальность полета соломы.

В свою очередь,

y₁ = r×cos (wt₁ ‑ a); (12)

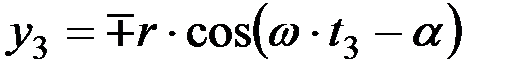. (13)

Дальность полета S_y может быть найдена как произведение горизонтальной составляющей скорости V_y на время полета, тогда

;

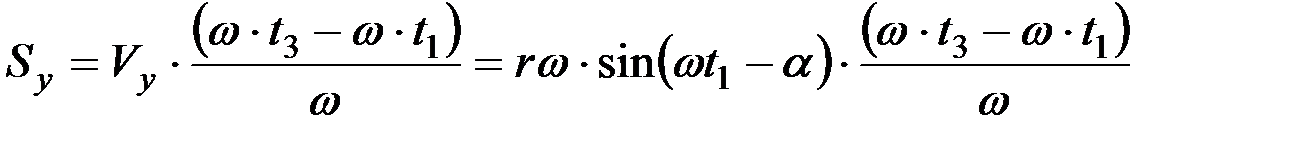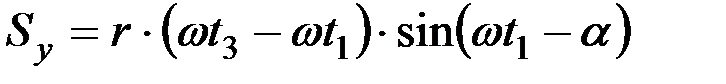. (14)

Теперь могут быть определены отрезки Dу_а и Dх_а:

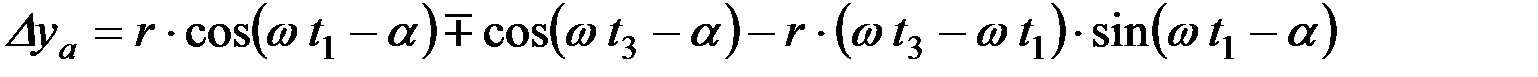; (15)

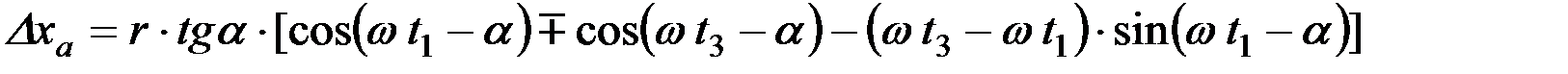. (16)

Если величины «отрезков» подставить в общее уравнение, то можно получить:

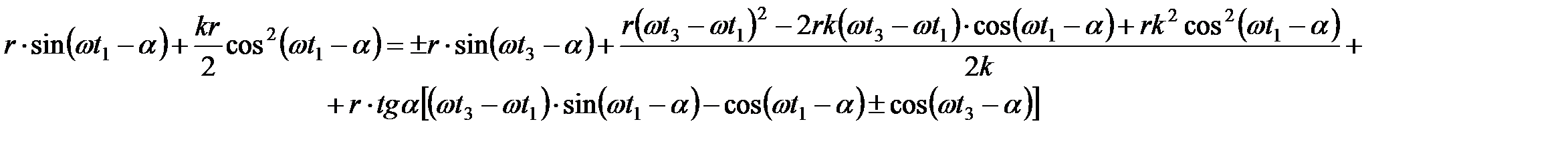. (17)

После приведения к общему знаменателю данное уравнение приводится к следующему виду

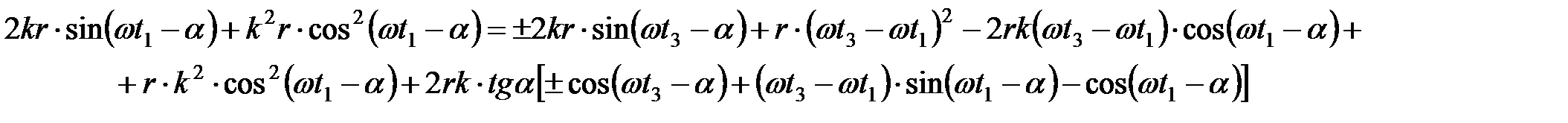. (18)

Данное соотношние представляет собой квадратное уравнение относительно разности фаз (wt ₃ - wt ₁):

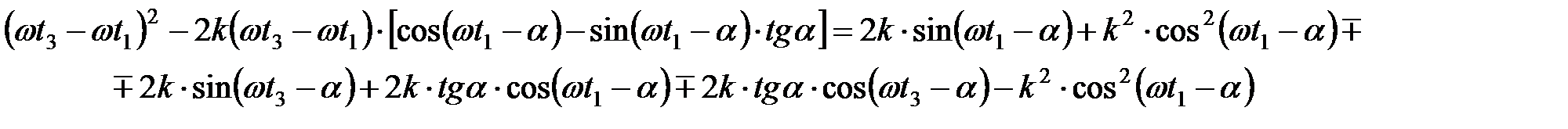. (19)

Преобразование коэффициента перед (wt ₃ - wt ₁) в левой части уравнения с учетом значения 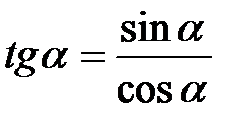и формул синуса и косинуса разности двух углов позволяет его значительно упростить:

.

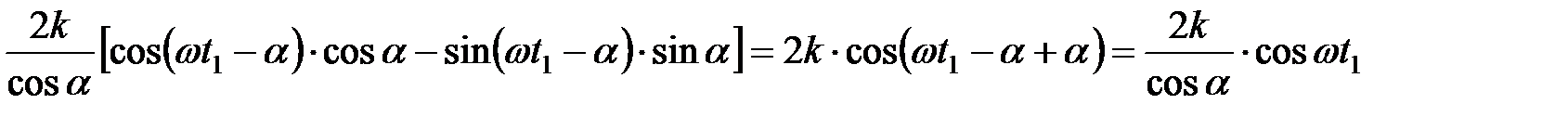Учитывая, что по первому основному уравнению соломотряса

,

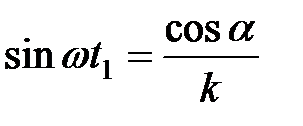левую часть уравнения (19) можно тогда привести к виду

.

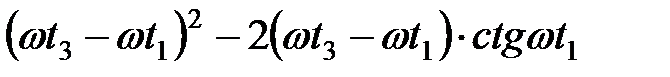Правую часть уравнения (19) можно преобразовать следующим образом:

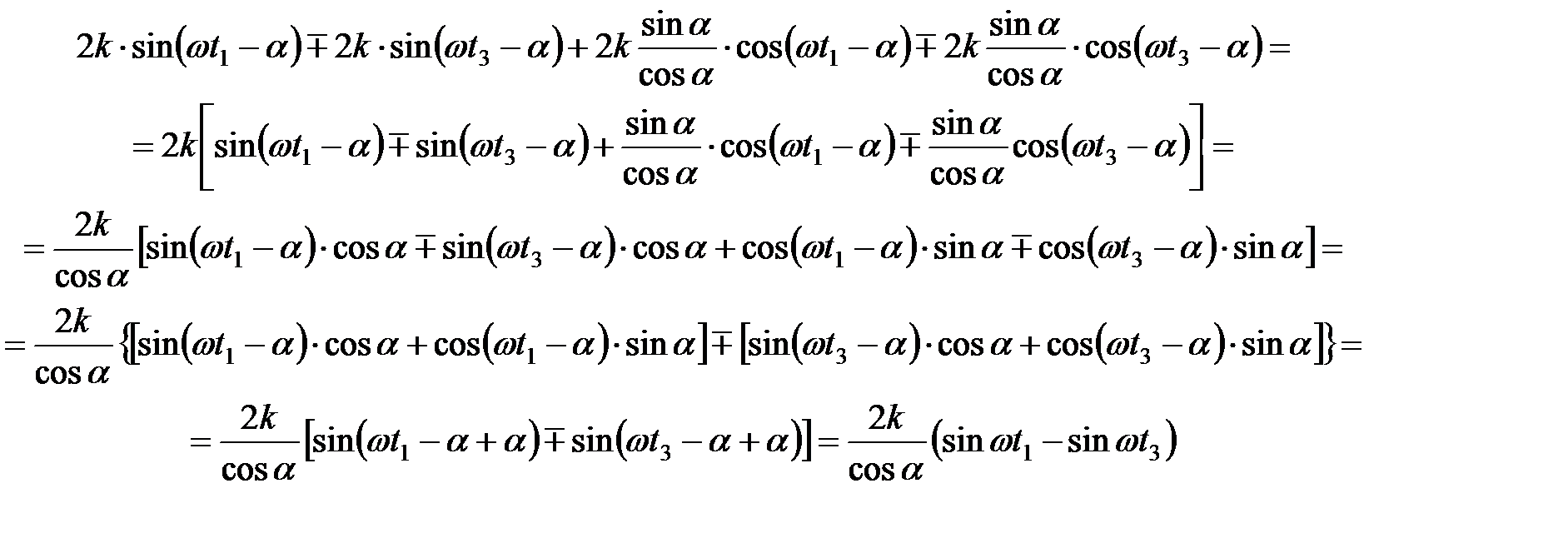. (20)

С учетом того, что 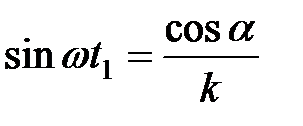, т.е. 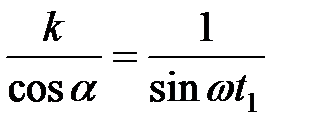последующий результат можно привести к виду

.

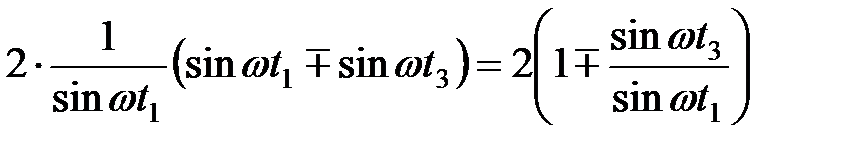Окончательно квадратное уравнение (19) может быть представлено так

.

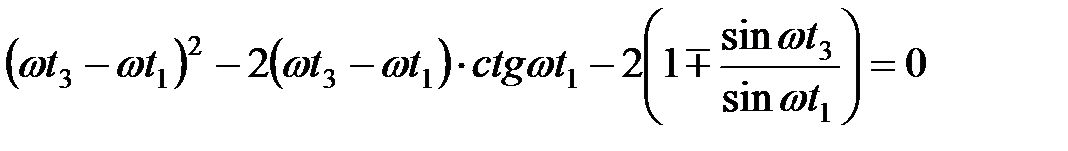После подстановки всех отрезков в исходное соотношение (6) формируется квадратное уравнение относительно разности фаз (wt₃-wt₁) решением, которого является

. (21)

Уравнение (21) является трансцендентным, так как не может быть решено относительно фазы wt₃, но приближенное его решение с любой заданной точностью на ЭВМ не составляет труда. В предложенной программе уравнение (21) решается методом дихотомии.

В подкоренном выражении перед последним слагаемым стоят знаки . Верхний знак используется в уравнении (17) в том случае, когда солома падает на ту же клавишу, которая ее подбросила, а нижний - если солома подброшена одной группой клавиш, а падает она на другую группу клавиш.

Дата добавления: 2015-06-04