Обоснование кинематического режима соломотряса

Основные уравнения соломотряса (5, 17), определяющие фазу отрыва wt₁ и соударения wt₃, могут быть использованы для выбора такого значения показателя кинематического режима k, при котором процесс выделения зерна из соломы будет эффективным. Правда, по вопросу выбора критерия эффективности режима работы соломотряса существуют различные мнения. Ряд авторов считает, что для более интенсивного выделения зерна необходимо наносить по слою хлебной массы сильные встречные удары поверхностью клавиши [1, 2]. Другие основное внимание обращают на необходимость создания вспушенного слоя грубого вороха, с тем чтобы зерно легче могло пройти через пространственную решетку, образованную отдельными соломинами. Результаты скоростной киносъемки процесса сепарации зерна показали, что наибольшее количество зерна выделяется через поверхность клавиши в момент начала удара соломы о клавишу, а это может подтвердить как первое, так и второе мнение.

Таким образом, можно согласиться с тем, что для осуществлении технологического процесса соломотряс должен наносить по соломе встречные удары и создавать вспушенный слой, повышающий вероятность выделения зерна. Встречные удары соломы и поверхность четырехклавишного соломотряса возможны лишь тогда, когда клавиши двигаются вверх, что имеет место, если фазa соударения окажется в пределах от wt₃=l,5p; до 2p + wt₁.

Для того чтобы определить показатели кинематического режима, при котором фаза соударения окажется в названных пределах, необходимо во второе уравнение соломотряса (17) подставить желательное значение фазы соударения, а фазу wt₁ представить в функции от показателя кинематического режима k и угла наклона соломотряса a по первому основному уравнению (5).

Например, пусть фаза соударения будет равна

wt₃ = 1,5p.

Если подставить это значение в уравнение (17)

,

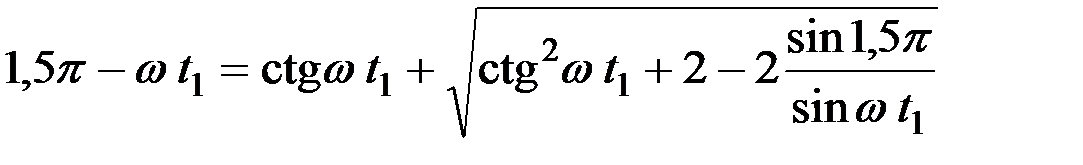то

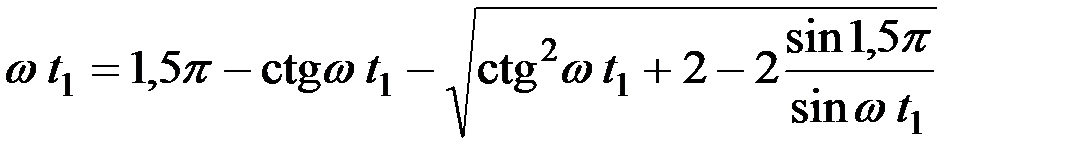
Учитывая, что по уравнению (5)

.

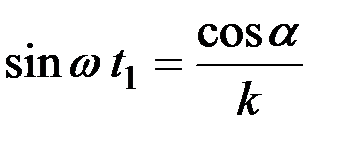Можно взять sin wt от левой и правой частей полученного равенства:

.

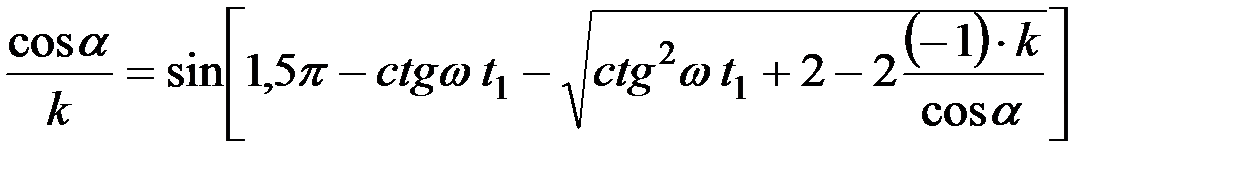Если известен sin wt₁, то нетрудно найти значение cos wt₁, а затем и ctg wt₁:

,

.

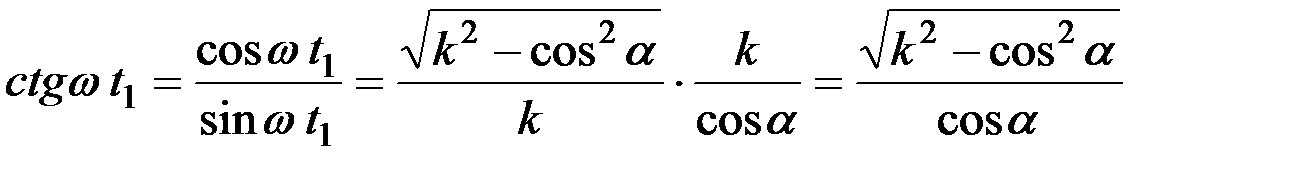После подстановки значения ctg wt₁ в уравнение можно получить

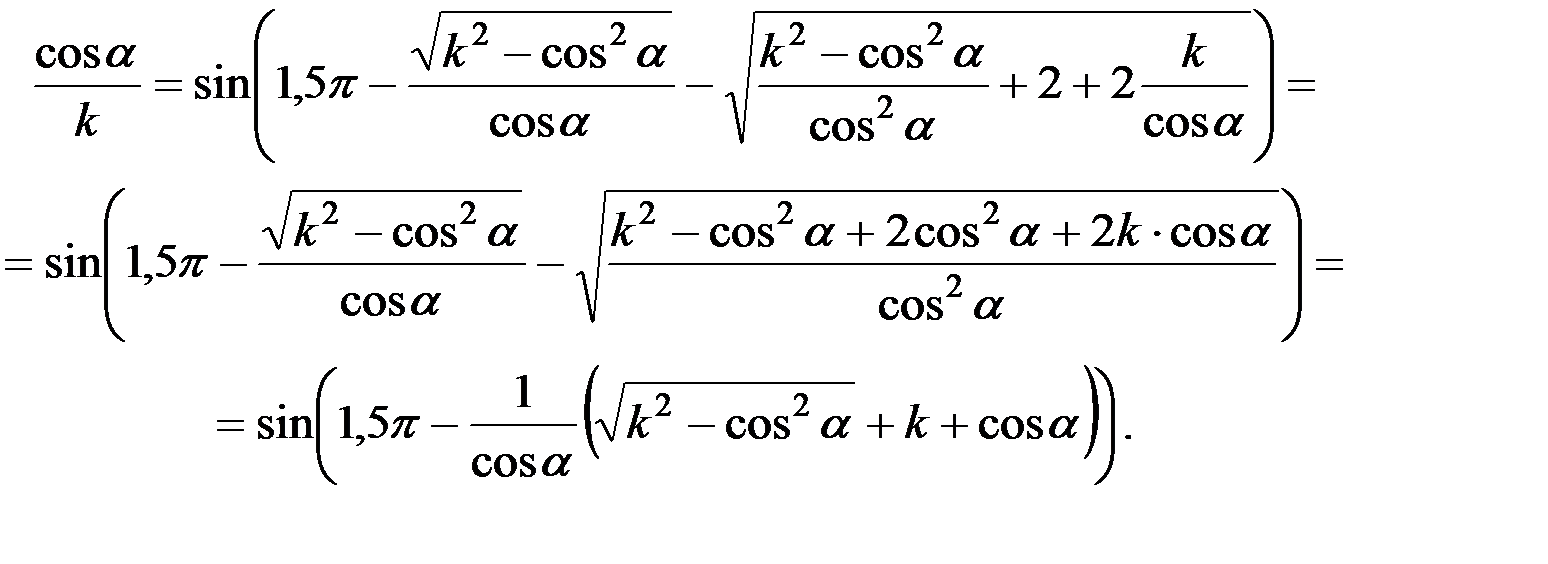(22)

Для горизонтального соломотряса это уравнение несколько упростится:

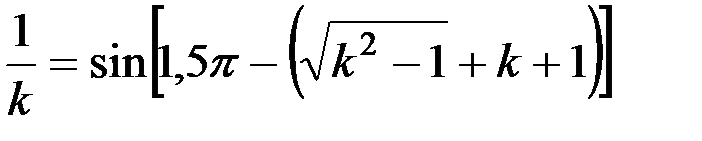. (23)

Корнем этого уравнения является значение k = 1,7.

Необходимо заметить, что при фазе соударения wt₃ = 1,5p величина вертикальной составляющей скорости соломотряса равна нулю, а следовательно, удары окажутся слабыми. Чтобы к моменту соударения скорость V_x увеличилась, необходимо фазу соударения иметь в пределах wt₃ = 2p (когда V_x максимально) или во всяком случае вблизи от 2p, например, 2p - wt₁ или 2p +wt₁.

Если wt₃ = 2p - wt₁, то, подставляя это значение в уравнение, (17), можно получить:

.

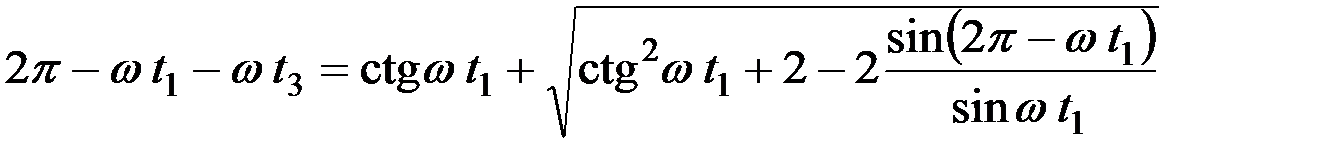Продолжая преобразования, аналогичные предыдущему случаю, можно найти

. (23)

Для горизонтального соломотряса это составит:

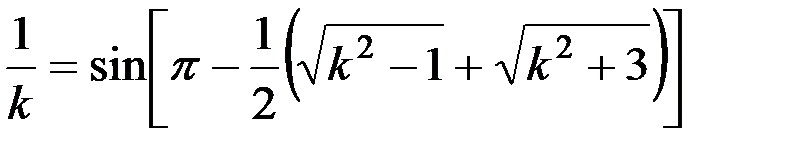. (24)

Подстановкой нетрудно убедиться, что корнем этого уравнения является k = 2,57.

Если wt₃ = 2p (когда вертикальная скорость клавиши наибольшая), то

;

.

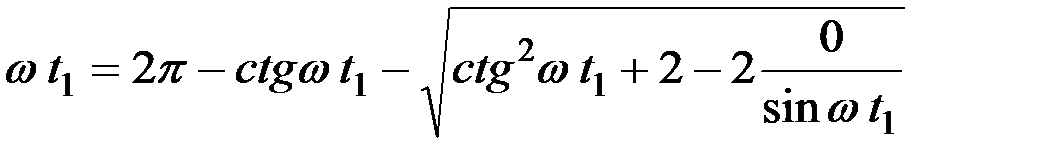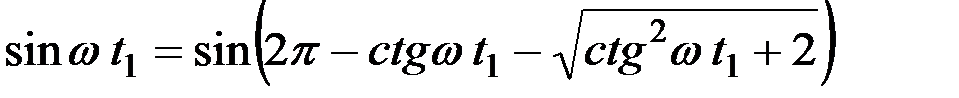Учитывая значения sin wt₁ и ctg wt₁, можно получить:

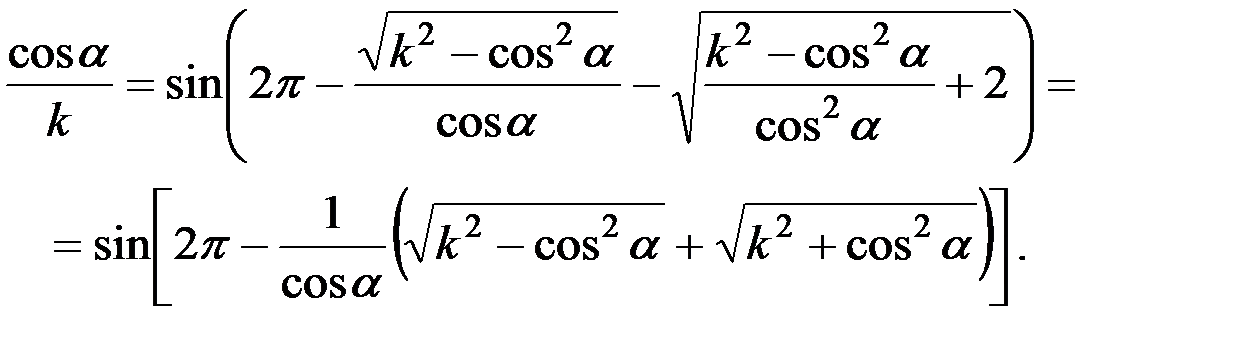(25)

Для горизонтального соломотряса уравнение (25) приобретает вид

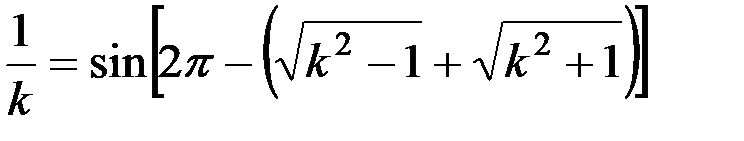. (26)

Корнем этого уравнения является k = 2,97. И наконец, предельное высокое значение wt₃ = 2p + wt₁. При такой фазе соударения солома практически непрерывно находится во взвешенном состоянии, так как отрывается от клавиши в фазе wt₁, а падает при wt₃ = 2p + wt₁, но эта фаза будет соответствовать wt₁ следующего оборота вала кривошипа, значит, солома опять оторвется от соломотряса в тот же момент времени:

wt₃ = 2p + wt₁.

Повторяя предшествующие преобразования, можно получить:

,

.

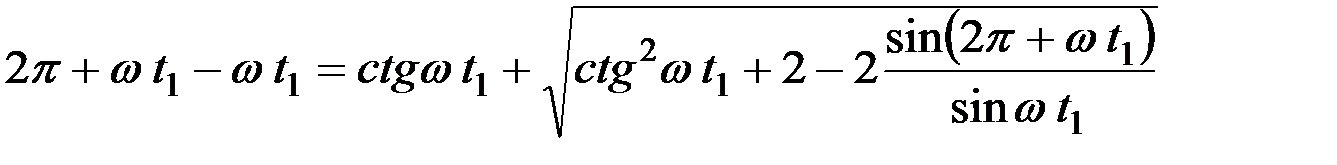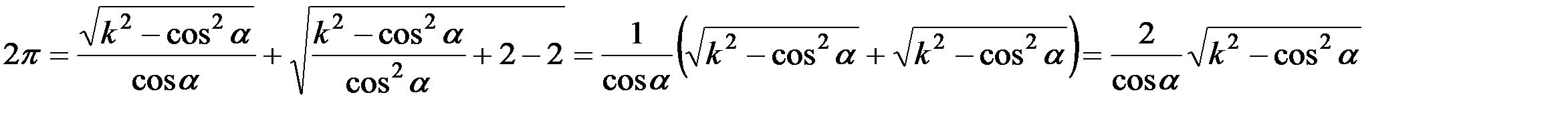После сокращения на 2 левой и правой частей получится

;

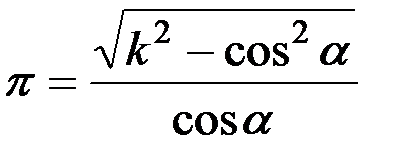или

,

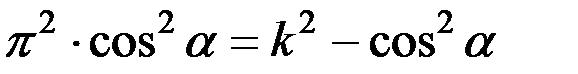тогда

. (27)

Для горизонтального соломотряса k = 3,3. (28)

Таким образом, для горизонтального четырехклавишного соломотряса возможные значения к находятся в пределах

1,7 < k < 3,3.

Для наклонного четырехклавишного соломотряса возможные значения изменяются согласно уравнениям (21), (23) и (27).

Если углу a придавать различные значения и вычислять k по этим уравнениям, то можно получить области возможных режимов наклонного соломотряса (рис. 6).

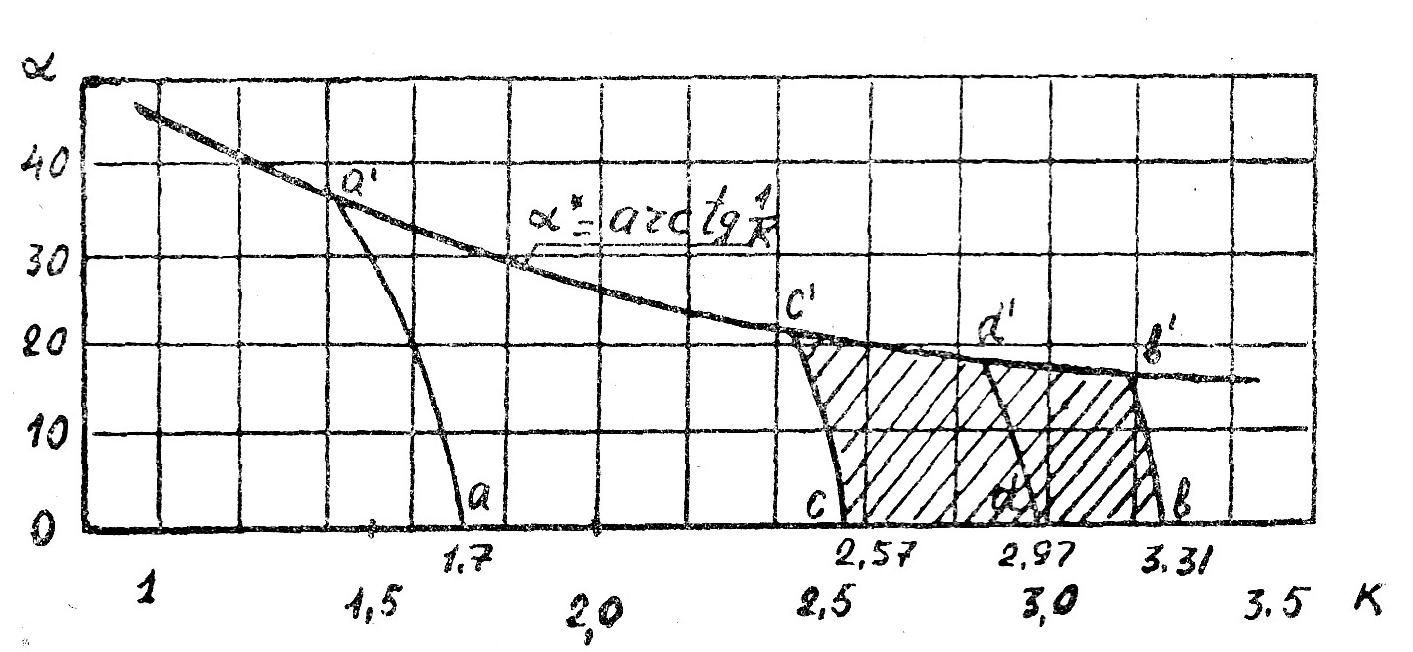
Рис. 6. Области возможных значений режимов наклонного четырехклавишного соломотряса

Изменение угла наклона a ограниченно, так как при чрезмерном наклоне клавиш соломотряс может оказаться неработоспособным.

В момент времени t₁ солома и клавиши обладают одинаковой линейной скоростью, направленной под углом b к горизонту, причем этот угол (рис. 5) определяется величиной

b = p/2‑ (wt₁ - a). (29)

После отрыва от соломотряса солома ведет себя как тело, брошенное под углом b к горизонту. Если угол b окажется равным p/2, то солома будет падать на то же место, с которого она была подброшена, т. е. перестанет перемещаться по клавишам, что приведет к забиванию соломотряса. Из уравнения (29) следует, что

b = p/2 при a* = wt₁,

где a* ‑ предельно возможное значение угла наклона соломотряса.

Поскольку по первому основному уравнению (5)

,

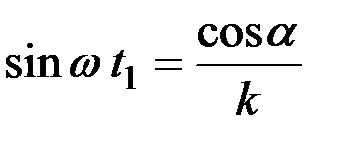то

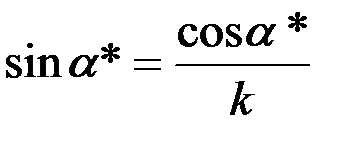
или

tg a* = 1/k.

Таким образом, чем больше величина показателя кинематического режима, тем меньшее значение угла наклона соломотряса допустимо. Например, при k = 1,7 работоспособность нарушается, если a* = arc tg 1/1,7 = 30,46°; а при k = 3,3a*= = 16,86°.

На рис. 6 предельный угол ограничивает области возможных режимов по линии a¢ b¢.

Характерные частные случаи и области типичных режимов пятиклавишных соломотрясов могут быть определены аналогичным образом. Но поскольку солома, подброшенная одной группой клавиш, у этого соломотряса падает на другую группу, то для того, чтобы получить встречные удары, необходимо иметь wt₃ в пределах от p до 1,5p.

Экспериментальное исследование движения соломы по клавишам с использованием скоростной киносъемки показало, что у четырехклавишного соломотряса действительные траектории частиц значительно отличаются от построенных по приведенным уравнениям [8]. Реальная дальность полета частиц, а следовательно, и средняя скорость перемещения соломы по клавишам выше расчетной в 5...10 раз в зависимости от условий опыта. Отличаются от расчетных значений и величины фаз отрыва и соударения. Так, при r = 0,05 м, n =195 мин^-1 угол отрыва должен составлять 27°, а в действительности нижняя часть слоя соломы отрывалась при wt₁ = 80°. При n = 215 мин^-1 эти фазы получились соответственно равными 22° и 70°. Естественно, что малые значения угла отрыва приведут к высоким и коротким траекториям, а при больших углах wt₁ солома падает вдоль соломотряса, что приводит к образованию пологих и длинных траекторий. Существует несколько предложений, направленных на уточнение теории движения вороха по соломотрясу

Для уточнения теории движения соломы стали учитывать реальное время соударения слоя вороха с клавишей соломотряса. Дело в том, что при подбрасывании слой соломы сильно вспушивается. Когда нижние слои при движении вниз уже коснутся клавиш и будут двигаться с ними кверху, верхние частицы могут еще продолжать движение вниз. И пока их движение вниз не закончится, солома не может оторваться от поверхности, даже если угол поворота коленчатого вала и превысил расчетное значение фазы wt₁.

На рис. 7 изображены в виде синусоиды график изменения положения клавиши во времени и парабола ‑ траектория движения соломы.

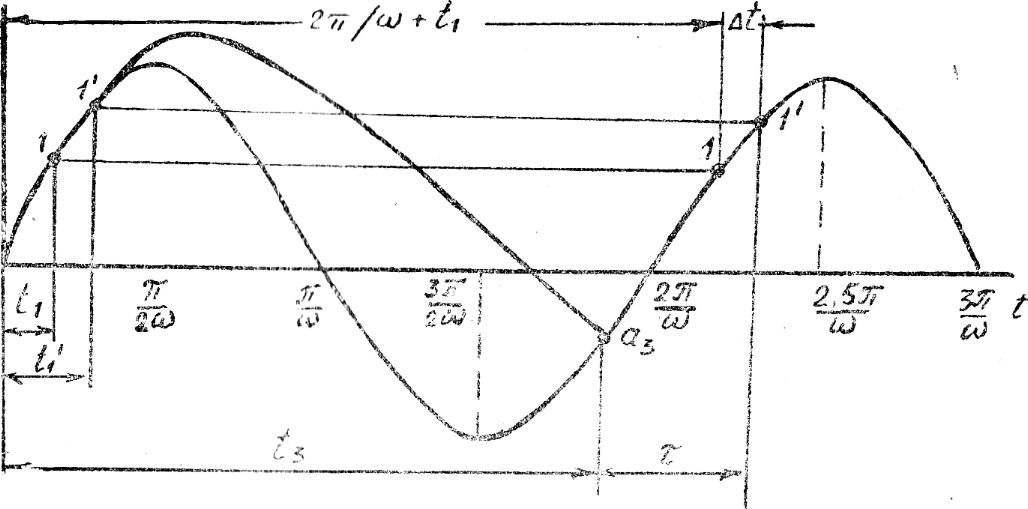
Рис. 7. Взаимодействие соломы и клавиш с учетом реальной продолжительности времени соударения

Если солома начнет падать на поверхность клавиши в точке а ₃, а продолжительность соударения t, то последующий отрыв частиц от соломы будет происходить не в расчетной точке 1 (рис. 8), а в 1¢, положение которой определится углом фазы wt₁.

Для определения уточненных значений фаз отрыва wt₁ и со ударения wt₃ используется тот же прием, с помощью которого эти фазы рассчитаны ранее.

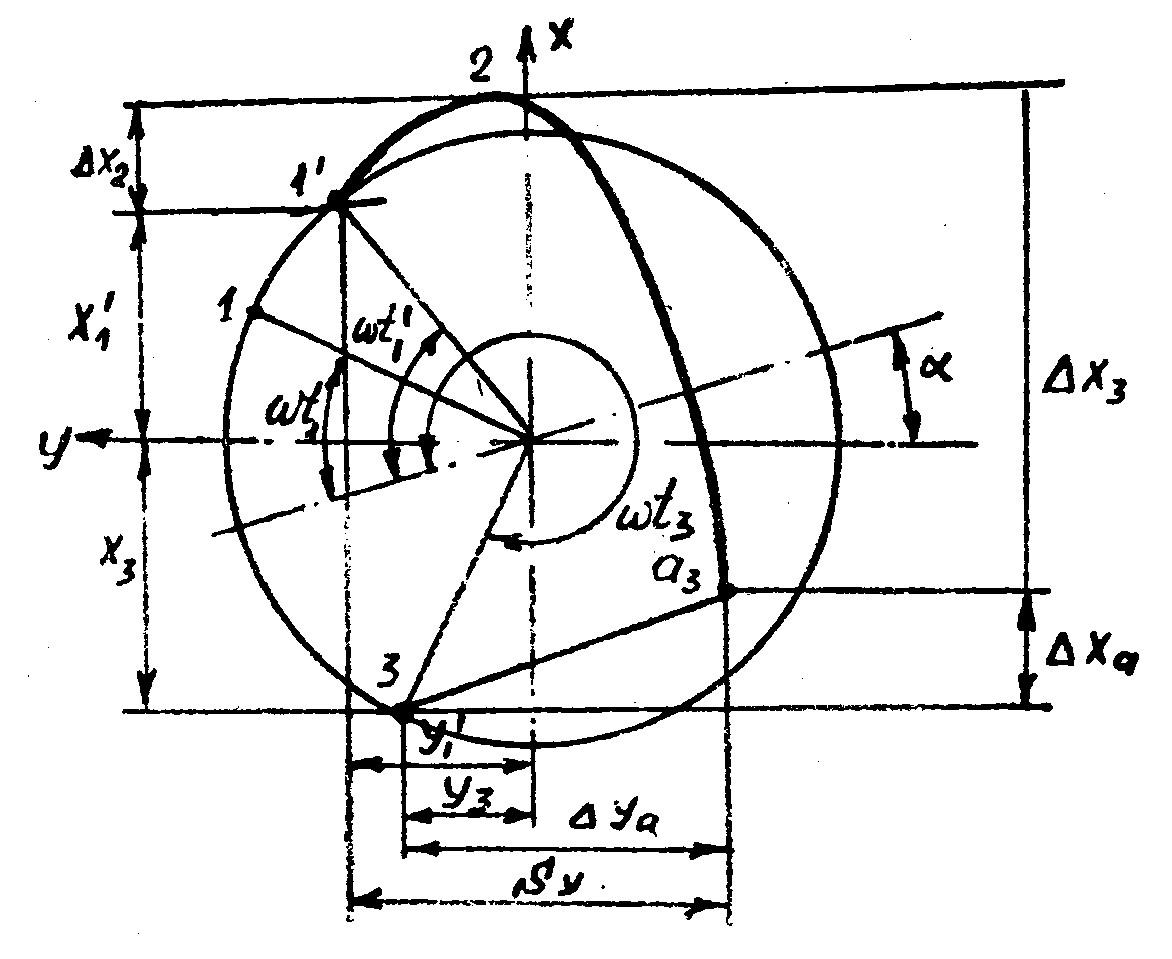
Рис. 8. Схема перемещения соломы за один оборот коленчатого вала с учетом продолжительности времени удара

Дата добавления: 2015-06-04