Решение уравнений для двух состояний

Теперь можно писать наше уравнение двух состояний в раз-jличных видах, например:

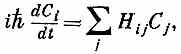
или вот так:

Оба они означают одно и то же. Для частицы со спином ¹/₂ в магнитном поле гамильтониан Н дается уравнением (9.8) или (9.13). I Если поле направлено по г, то, как мы уже много раз видели, решение заключается в том, что состояние |y>, каким бы оно ни было, прецессирует вокруг оси z (в точности, как если бы взять \ физическое тело и вращать его как целое вокруг оси z) с угловой

скоростью, вдвое большей, чем mB/h. Все это, конечно, относится и к магнитному полю, направленному под другим углом, ведь физика от системы координат не зависит. Если магнитное поле время от времени как-то сложно меняется, то такое положение пещей можно анализировать следующим образом. Пусть вначале спин был в направлении +z, а магнитное поле — в направле­нии х. Спин начал поворачиваться. Если выключить x -поле, поворот прекратится. Если теперь включить z-поле, спин начнет поворачиваться вокруг z и т. д. Значит, смотря по тому, как меняются поля во времени, вы можете представить себе, каким будет конечное состояние — по какой оси оно будет направлено. Затем можно отнести это состояние к первоначальным |+> и |-> по отношению к z, пользуясь проекционными формулами, полученными в гл. 8 (или в гл. 4). Если в конечном состоянии спин направлен по (q, j), то амплитуда того, что спин будет смотреть вверх, равна 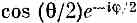, а амплитуда того, что спин будет смотреть вниз, равна 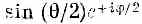. Это решает любую задачу. Таково словесное описание решений дифференциальных уравнений.

Только что описанное решение достаточно общо для того. чтобы справиться с любой системой с двумя состояниями. Возь­мем наш пример с молекулой аммиака, на которую действует электрическое поле. Если система описывается на языке состоя­ний | I > и | II >, то уравнения выглядят так:

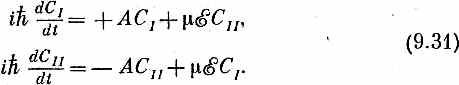
Вы скажете: «Нет, там, я помню, стояло еще E ₀». Неважно, мы просто сдвинули начало отсчета энергий, чтобы Е ₀стало равно нулю. (Это всегда можно сделать, изменив обе амплитуды в одно и то же число раз — в e^iE0T/h; так можно избавить­ся от любой постоянной добавки к энергии.) Одинаковые урав­нения обладают одинаковыми решениями, поэтому не стоит решать их вторично. Если взглянуть на эти уравнения и на (9.1), то их можно отождествить между собой следующим образом. Состояние |+> обозначим | I >, состояние |-> обозначим | Н >. Это вовсе не значит, что мы выстраиваем аммиак в про­странстве в одну линию или что |+> и |-> как-то связаны с осью z. Это все делается чисто искусственно. Имеется искусст­венное пространство, которое можно было бы назвать, например, «модельным пространством молекулы аммиака» или еще как-нибудь иначе. Это просто трехмерная «диаграмма», и направле­ние «вверх» означает пребывание молекулы в состоянии | I >, а направление «вниз» по фальшивой оси z означает пребывание молекулы в состоянии | II >. Тогда уравнения отождествляются следующим образом.

Прежде всего вы видите, что гамильтониан может быть записан через матрицы сигма:

Если сравнить это с (9.1), то m B_z будет соответствовать - А, а m В_х будет соответствовать -mx. В нашем «модельном» про­странстве возникает, стало быть, постоянное поле В, направ­ленное по оси z. Если есть, кроме этого, электрическое поле x, меняющееся со временем, то у поля В появится и пропорцио­нально меняющаяся x -компонента. Таким образом, поведение электрона в магнитном поле с постоянной составляющей в на­правлении z и колеблющейся составляющей в направлении х математически во всем подобно и точно соответствует поведе­нию молекулы аммиака в осциллирующем электрическом поле, К сожалению, у нас нет времени входить глубже в детали этого соответствия или разбираться в каких-либо технических дета­лях. Мы только хотели подчеркнуть, что можно сделать так, чтобы все системы с двумя состояниями были аналогичны объек­ту со спином ¹/₂, прецессирующему в магнитном поле.

Дата добавления: 2015-06-04