Проекционная матрица для спина 1. Состояния в магнитном поле

Состояния в магнитном поле

Зеемановское расщепление

Уровни энергии

Гамильтониан основного со­стояния водорода

Базисные состо­яния для системы двух частиц со спином 1/2

СВЕРХТОНКОЕ РАСЩЕПЛЕНИЕ В ВОДОРОДЕ

Среди новых частиц есть барион W- со странностью -3.—Прим. ред.

Читайте: «.K-нуль с чертой».

Свободная L-частица медленно распадается путем слабого взаимо­действия (так что странность не обязана при этом сохраняться). Про­дуктами распада могут быть либо р и p-, либо n и p0. Время жизни 2,2•10-10сек.

Если, конечно, он не создает еще двух К+ или других частиц с общей странностью +2. Можно считать, что здесь речь идет о реакциях, в которых не хватает энергии для возникновения этих добавочных стран­ных частиц.

Типичное время для сильного взаимодействия ближе к 10-23 сек.

Такую интерференцию действительно наблюдали. Коэффициент a оказался равным — 0,96b. Отсюда можно было вычислить и разность масс К1- и K2-мезонов. Она оказалась равной около —0,35•10-5 эв. Это наимень­шая разность масс двух частиц, известных физикам.— Прим. ред.

* Мы здесь упрощаем. Система 2p может иметь множество состоя­ний, отвечающих различным импульсам p-мезонов, и в правой части >того равенства следовало бы поставить сумму по всем базисным состоя­ниям p-мезонов. Но полный вывод все равно приводит к тем же резуль­татам.

* Это похоже на то, что мы обнаружили (в гл. 4) для частиц со спи­ном ¹/₂. когда поворачивали систему координат вокруг оси z; тогда мы получили фазовые множители exp (±ij/2). В действительности это в точ­ности то же самое, что мы писали в гл. 3, § 7, для состояний |+> и |-> частицы со спином 1, и это не случайно. Фотон— это частица со спи­ном 1, у которой, однако, нет «нуль»-состояния.

** Мы сознаем, что материал этого параграфа длиннее и труднее, чем это положено на нашем уровне знаний. Лучше пропустите его и пере­ходите прямо к § 6. Но если у вас есть самолюбие и время, попозже вер­нитесь к нему опять. Это великолепнейший пример (взятый к тому же из последних работ по физике высоких энергий) того, что можно сотворить с помощью нашей формулировки квантовой механики двухуровневых систем. (Для русского издания параграф переделан проф. Сэндсом. — Прим. ред.)

* Параграф 5 при первом чтении книги можно пропустить. Он сложнее, чем положено в таких курах.

Глава 10

§ 1. Базисные состояния для системы двух частиц со спином ¹/₂

В этой главе мы займемся «сверхтонким расщеплением» водорода — интересным при­мером того, что мы уже в состоянии делать с помощью квантовой механики. Здесь у нас уже будут не два состояния, а больше. Поучи­тельность этого примера в том, что он познако­мит нас с методами квантовой механики, приме­няемыми в более сложных задачах. Сам по себе этот пример достаточно сложен, и как только вы поймете, как с ним справляться, вам сразу же станет ясно, как обобщить его на другие воз­можные задачи.

Как известно, атом водорода состоит из электрона и протона; электрон сидит неподалеку от протона и может существовать в одном из многих дискретных энергетических состояний, в каждом из которых его картина движения дру­гая. Так, первое возбужденное состояние лежит на ³/₄ ридберга, или на 10 эв, выше основного состояния. Но даже так называемое основное состояние водорода на самом деле не является отдельным состоянием с определенной энергией, ибо у электрона и у протона есть спины. Эти спины и ответственны за «сверхтонкую струк­туру» в уровнях энергии, которая расщепляет все уровни энергии на несколько почти одина­ковых уровней.

Спин электрона может быть направлен либо вверх, либо вниз; у протона тоже его собствен­ный спин может смотреть вверх или вниз. Поэтому на всякое динамическое состояние атома приходятся четыре возможных спиновых состояния. Иначе говоря, когда физик говорит об «основном состоянии» водорода, он на самом деле имеет в виду «четыре основных состояния», а не просто самое низкое из них. У четырех спиновых состояний энергия не совсем одинакова; имеются небольшие сдвиги по от­ношению к тому, что наблюдалось бы в отсутствие спинов. Эти сдвиги, однако, во много-много раз меньше, чем те 10 эв, которые лежат между основным состоянием и следующим более высоким состоянием.

В итоге энергия каждого динамического состояния расщеп­лена на ряд очень тесных уровней — это так называемое сверх­тонкое расщепление.

Разности энергий четырех спиновых состояний — это и есть то, что мы хотим рассчитать в этой главе. Сверхтонкое расщеп­ление вызывается взаимодействием магнитных моментов элек­трона и протона; оно приводит для каждого спинового состояния к слегка отличающимся магнитным энергиям. Эти сдвиги энер­гии составляют только около десятимиллионной части электрон-вольта, что действительно много меньше 10 эв!

Именно из-за столь большого промежутка основное состоя­ние водорода мы вправе считать «четырехуровневой системой», не заботясь о том, что на самом-то деле при более высоких энер­гиях состояний куда больше. Мы намерены ограничиться здесь изучением сверхтонкой структуры только основного состояния атома водорода.

Для наших целей нам неважны различные детали расположе­ния электрона и протона, потому что все они, так сказать, уже выработаны атомом, все они получились сами собой, когда атом попал в основное состояние. Достаточно знать только, что элек­трон и протон находятся невдалеке друг от друга, в каком-то определенном пространственном соотношении. Кроме того, у них могут быть всевозможные взаимные ориентации спинов. И мы хотим рассмотреть только спиновые эффекты.

Первый вопрос, на который нужно ответить: каковы базис­ные состояния для этой системы? Но вопрос этот поставлен не­правильно. Такой вещи, как единственный базис, не существует, а всякая система базисных состояний, которую вы выберете, не будет единственной. Всегда можно составить новые систе­мы из линейных комбинаций старой. Для базисных состоя­ний всегда есть множество выборов и все они одинаково законны.

Значит, надо спрашивать: не «каков базис?», а «каким его можно выбрать?». И выбрать вы вправе какой угодно, лишь бы вам было удобно.

Обычно лучше всего начинать с базиса, который физи­чески наиболее очевиден. Он не обязательно должен решать какую-то задачу или быть непосредственно важным в каком-то отношении, нет, он в общем должен только облегчать пони­мание того, что происходит.

Мы выбираем следующие базисные состояния:

Состояние 1. И у электрона, и у протона спины смотрят вверх.

Состояние 2. У электрона спин смотрит вверх, а у протона— вниз.

Состояние 3. У электрона спин смотрит вниз, а у протона —

вверх.

Состояние 4. И у электрона, и у протона спины смотрят

вниз.

Для краткой записи этих четырех состояний введем следую­щие обозначения:

Состояние 1: |+ +>; у электрона спин вверх, у протона спин вверх.

Состояние 2: | + ->; у электрона спин вверх,

у протона спин вниз.

Состояние 3: |- + >; у электрона спин вниз, у протона спин вверх.

Состояние 4: | - ->; у электрона спин вниз, у протона спин вниз. (10.1)

Помните, что первый знак плюс или минус относится к элек­трону, второй — к протону. Чтобы эти обозначения были у вас под рукой, они сведены на фиг. 10.1.

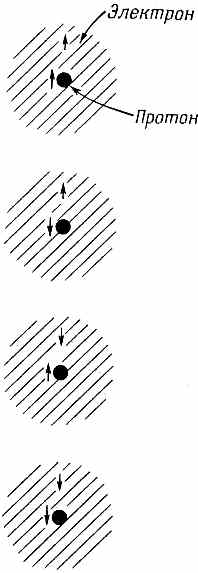
Фиг. 10.1. Совокупность базисных состояний

для основного состояния атома водорода.

Эти состояния мы обозначаем | + +>, | + ->> |- +>.

Временами будет удобнее обозначать эти состояния |1>, |2>, |3> и |4>.

Вы можете сказать: «Но частицы взаимодействуют, и, может быть, эти состояния вовсе не являются правильными базисными состояниями. Получается, будто вы рассматриваете обе частицы независимо». Да, действительно! Взаимодействие ставит перед нами вопрос: каков гамильтониан системы? Но вопрос о том, как описать систему, не касается взаимодействия. Что бы мы ни выбрали в качестве базиса, это никак не связано с тем, что слу­чится после. Может оказаться, что атом не способен оставаться в одном из этих базисных состояний, даже если с него все и на­чалось. Но это другой вопрос. Это вопрос о том, как со временем меняются амплитуды в выбранном (фиксированном) базисе. Вы­бирая базисные состояния, мы просто выбираем «единичные векторы» для нашего описания.

Раз уже мы коснулись этого, бросим взгляд на общую проб­лему отыскания совокупности базисных состояний, когда имеет­ся не одна частица, а больше. Вы знаете базисные состояния для одной частицы. Электрон, например, полностью описывается в реальной жизни (не в наших упрощенных случаях, а в реаль­ной жизни) заданием амплитуд пребывания в одном из следующих состояний:

| Электрон спином вверх с импульсом р> или

| Электрон спином вниз с импульсом р>.

В действительности существуют две бесконечные совокупности состояний, по одному на каждое значение р. Значит, сказать, что электронное состояние |y> описано полностью, можно лишь тогда, когда вы знаете все амплитуды

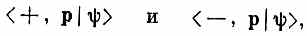
где + и - представляют компоненты момента количества движения вдоль ка­кой-то оси, обычно оси z, a p — вектор импульса. Стало быть, для каждого мыс­лимого импульса должны быть две ампли­туды (дважды бесконечная совокупность базисных состояний). Вот и все, что нужно для описания отдельной частицы.

Таким же образом могут быть написаны базисные состояния, когда частиц не одна, а больше. Например, если надо было бы рассмотреть электрон и протон в более сложном, чем у нас, слу­чае, то базисные состояния могли бы быть следующими: Электрон с импульсом p₁ движется спином вверх, а протон с импульсом р₂ движется спином вниз. И так далее для других спиновых комбинаций. Если частиц больше двух, идея остается та же. Так что вы видите, что распи­сать возможные базисные состояния на самом деле очень легко. Вопрос только в том, каков гамильтониан.

Нам для изучения основного состояния водорода нет нужды применять полные совокупности базисных состояний для раз­личных импульсов. Мы оговариваем и фиксируем определенные импульсные состояния протона и электрона, когда произносим слова «основное состояние». Детали конфигурации — амплиту­ды для всех импульсных базисных состояний — можно рассчи­тать, но это уже другая задача. А мы сейчас касаемся только влияния спина, так что ограничимся только четырьмя базис­ными состояниями (10.1). Очередной вопрос таков: каков га­мильтониан для этой совокупности состояний?

Дата добавления: 2015-06-04