Обобщение на системы с N состояниями

Мы покончили с системами с двумя состояниями, рассказав все, что хотелось. В дальнейших главах мы перейдем к изуче­нию систем с большим числом состояний. Расширение на систе­мы с N состояниями идей, разработанных для двух состояний, проходит довольно просто. Это делается примерно так.

Если система обладает N различными состояниями, то всякое состояние |y(t)>можно представить как линейную комбина­цию произвольной совокупности базисных состояний | t >, где i =l, 2, 3,..., N:

Коэффициенты C_i (t) — это амплитуды < i |y(t)>. Поведение амплитуд С_i во времени направляется уравнениями

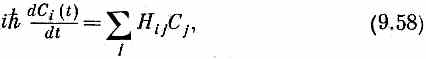
где энергетическая матрица H_ij описывает физику задачи. С виду она такая же, как и для двух состояний. Но только теперь и i, и j должны пробегать по всем N базисным состоя­ниям, и энергетическая матрица H_ij (или, если вам больше нравится, гамильтониан) — это теперь матрица NXN, состоя­щая из N ²чисел. Как и прежде, H_ij=H_ji (до тех пор, пока частицы сохраняются) и диагональные элементы H_ii суть ве­щественные числа.

Мы нашли общее решение для всех С в системе с двумя со­стояниями, когда энергетическая матрица постоянна (не зави­сит от t). Точно так же нетрудно решить и уравнение (9.58) для системы с N состояниями, когда Н не зависит от времени. Опять мы начинаем с того, что ищем возможное решение, в кото­ром у всех амплитуд зависимость от времени одинакова. Мы про­буем

Если все эти C_i подставить в (9.58), то производные dC_i (t) /dt превращаются просто в (- i/h)EC_i. Сокращая повсюду на общую экспоненту, получаем

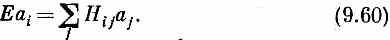
Эта система N линейных алгебраических уравнений для N неизвестных a ₁ а ₂,..., а_n;решение у нее бывает только тогда, когда вам сильно повезет, когда определитель из коэффициентов при всех а равен нулю. Но не нужно чересчур умничать: можете просто начать их решать любым способом, и вы сразу увидите, что решить их удается лишь при некоторых значениях E. (Вспомните, что единственная величина, которая в этих уравне­ниях подлежит подгонке, это Е.)

Если, впрочем, вы хотите, чтобы все было по форме, пере­пишите (9.60) так:

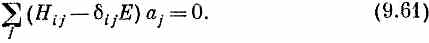
Затем примените правило (если оно вам знакомо), что эти урав­нения будут иметь решения лишь для тех значений Е, для кото­рых

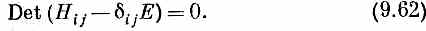
Каждый член в детерминанте — это просто H_ij и только из диагональных отнято Е. Иначе говоря, (9.62) означает просто

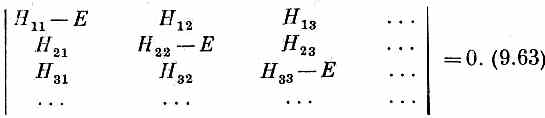
Это, конечно, всего-навсего особый способ записывать алгебраи­ческие уравнения для Е, складывая вереницы членов, пере­множаемых в определенном порядке. Эти произведения дадут все степени Е вплоть до E^N.

Значит, у нас есть многочлен N- йстепени, который равняется нулю. У него, вообще говоря, есть N корней. (Нужно помнить, однако, что некоторые из них могут быть кратными корнями; это значит, что два или более корней могут быть равны друг другу.) Обозначим эти N корней так:

(пусть n обозначает n-е порядковое числительное, так что n принимает значения I, II,..., N). Некоторые из этих энергий могут быть между собой равны, скажем Е_II=Е_III, но мы решили все же обозначать их разными именами.

Уравнения (9.60) или (9.61) имеют по одному решению для каждого значения Е [из (9.64)]. Если вы подставите любое из Е, скажем E_n, в (9.60) и найдете все а_i, то получится ряд чисел а_i, относящихся к энергии E_n. Этот ряд мы обозначим а_i (n).

Если подставить эти а_i (n) в (9.59), то получатся амплитуды С_i (n) того, что состояния с определенной энергией находятся в базисном состоянии | i >. Пусть | n > обозначает вектор состоя­ния для состояния с определенной энергией при t= 0. Тогда можно написать

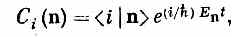
где

Полное состояние с определенной энергией |y_n(t)> можно тогда записать так:

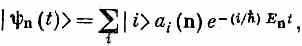
или

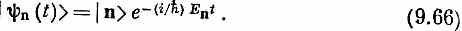
Векторы состояний | n > описывают конфигурацию состояний с определенной энергией, но с вынесенной зависимостью от вре­мени. Это постоянные векторы, которые, если мы захотим, можно использовать в качестве новой базисной совокупности.

Каждое из состояний | n > обладает тем свойством (в чем легко убедиться), что при действии на него оператором Гамиль­тона Н получится просто Е_n, умноженное на то же состояние:

Значит, энергия Е_n — это характеристическое число опера­тора Гамильтона Н^. Как мы видели, у гамильтониана в об­щем случае бывает несколько характеристических энергий. Фи­зики обычно называют их «собственными значениями» мат­рицы Н. Для каждого собственного значения Н^, иными словами, для каждой энергии, существует состояние с определенной энергией, которое мы называли «стационарным». Состояния | n > обычно именуются «собственными состояниями Н^». Каждое собственное состояние отвечает определенному собственному значению Е_n.

Далее, состояния | n > (их N штук) могут, вообще говоря, тоже быть выбраны в качестве базиса. Для этого все состояния должны быть ортогональны в том смысле, что для любой нары их, скажем | n > и | m),

< n | m >=0. (9.68)

Это выполнится автоматически, если все энергии различны. Кроме того, можно умножить все а_i (n) на подходящие множи­тели, чтобы все состояния были отнормированы: чтобы для всех n было

< n | n >=1. (9.69)

Когда оказывается, что (9.63) случайно имеет два (или боль­ше) одинаковых корня с одной и той же энергией, то появляются небольшие усложнения. По-прежнему имеются две различные совокупности а_i, отвечающие двум одинаковым энергиям, но состояния, которые они дают, не обязательно ортогональны. Пусть вы проделали нормальную процедуру и нашли два стацио­нарных состояния с равными энергиями. Обозначим их |m>и |v>. Тогда они не обязательно окажутся ортогональными: если вам не повезло, то обнаружите, что

<m|v>¹0.

Но зато всегда верно, что можно изготовить два новых состоя­ния (обозначим их | m'> и |v'>) с теми же энергиями, но орто­гональных друг другу:

<m'|v'>=0. (9.70)

Этого можно добиться, составив |m'> и |v'> из подходящих линейных комбинаций |m> и |v> с так подобранными коэффи­циентами, что (9.70) будет выполнено. Это всегда полезно де­лать, и мы будем вообще предполагать, что это уже проделано, так что можно будет считать наши собственноэнергетические состояния | n > все ортогональными.

Для интереса докажем, что когда два стационарных состоя­ния обладают разными энергиями, то они действительно ортого­нальны. Для состояния | n > с энергией Е_n

Это операторное уравнение на самом деле означает, что имеется соотношение между числами. Если заполнить недостающие части, то оно означает то же самое, что и

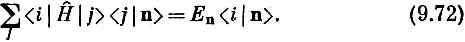
Проделав здесь комплексное сопряжение, получим

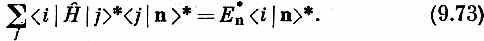
Теперь вспомним, что комплексно сопряженная амплитуда — это амплитуда обратного процесса, так что (9.73) можно пе­реписать в виде

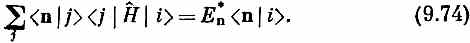
Поскольку это уравнение справедливо для всякого i, то его можно «сократить» до

Это уравнение называется сопряженным с (9.71).

Теперь легко доказать, что Е_n— число вещественное. Умножим (9.71) на < n |. Получится

(с учетом, что < n | n >=1). Умножим теперь (9.75) справа на

| n >:

Сравнивая (9.76) с (9.77), видим, что

Е_n=Е_n*, (9.78)

а это означает, что E _n вещественно. Звездочку при Е_n в (9.75) можно убрать.

Теперь наконец-то мы в силах доказать, что состояния с различными энергиями ортогональны. Пусть | n > и | m > — пара базисных состояний с определенными энергиями. Написав (9.75) для состояния | m > и умножив его на | n >, получим

Но если (9.71) умножить на < m |, то будет

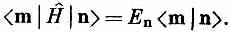
Раз левые части этих уравнений равны, то равны и правые:

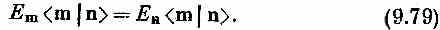
Если Е_m=Е_n, то это равенство ни о чем не говорит. Но если энергии двух состояний | m > и | n > различны (Е_m¹Е_n), то урав­нение (9.79) говорит, что < m | n > должно быть нулем, что мы и хотели доказать. Два состояния обязательно ортогональны, если только Е_n и Е_m отличаются друг от друга.

Дата добавления: 2015-06-04