Простейшие типы дифференциальных уравнений

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ.

Дифференциальным уравнением (ДУ) называется уравнение, которое помимо неизвестных функций содержит их производные (или дифференциалы).

Если неизвестные функции, входящие в ДУ, зависят только от одной независимой переменной, то ДУ называется обыкновенным ДУ (ОДУ).

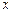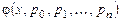Другими словами: пусть - независимая переменная, - искомая функция, - заданная функция переменных. Уравнение

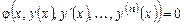, (1.1)

где 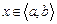называется обыкновенным дифференциальным уравнением относительно функции на промежутке .

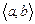Если 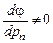, то число n называется порядком уравнения (1.1).

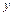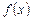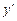Функция называется частным решением ОДУ (1.1), если после замены на 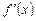, 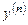на ,..., на 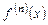уравнение обращается в тождество на промежутке 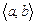. (Предполагается, что 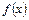- достаточно гладкая функция.)

Например, функция является решением уравнения 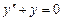на всей оси ОX.

В самом деле, подставив в уравнение 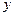и 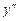, получим тождество: .

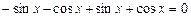График решения дифференциального уравнения называется интегральнойкривой этого уравнения. ДУ вида

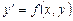, (1.2)

где 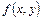определена в области D на плоскости XOY, называется ОДУ первого порядка, разрешенным относительно производной.

Задачей Коши называют задачу нахождения решения 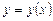уравнения (1.2), удовлетворяющего начальному условию

, где .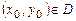

Геометрически это означает, что ищется интегральная кривая, проходящая через заданную точку .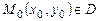

Теорема существования и единственности решения задачи Коши. Пусть дано дифференциальное уравнение 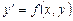, где функция 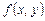определена в некоторой области D плоскости XOY, содержащей точку 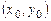. Если функция 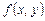удовлетворяет условиям:

а) 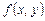есть непрерывная функция двух переменных 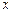и 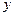в области D,

б) 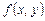имеет частную производную 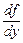, ограниченную в области D; то найдётся интервал 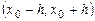, на котором существует единственное решение 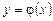данного уравнения, удовлетворяющее условию .

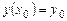Теорема даёт достаточные условия существования единственного решения задачи Коши для уравнения 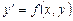, но эти условия не являются необходимыми, т.е. может существовать единственное решение уравнения 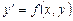, удовлетворяющее условию 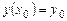, хотя в точке 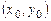не выполняются условия а) или б).

Пример 1.1. 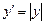. Здесь 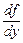не существует при .

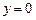Условие б) не выполняются, так как частная производная имеет разрыв при 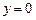(на оси OX). Тем не менее, через каждую точку оси 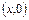проходит единственная интегральная кривая .

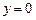Вместе с тем, совсем отбросить условие б) нельзя.

Пример 1.2. , .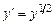

Частная производная 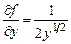не ограничена при 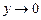, т.е. условие б) не выполнено. Рассматриваемая задача Коши имеет два решения

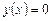и ,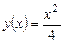

что проверяется подстановкой в уравнение.

Общим решением дифференциального уравнения 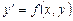называется функция 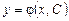, зависящая от одной произвольной постоянной С, если

1) функция удовлетворяет дифференциальному урав-нению при любых допустимых значениях С;

2) для любого частного решения уравнения (1.2) можно подобрать постоянную C, такую, что 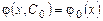на .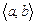

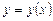Общим интегралом ОДУ (1.2) называется соотношение вида , если функция , найденная из него, есть общее решение ОДУ (1.2). Функция трех переменных 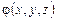считается определенной на множестве , .

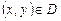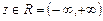Общее решение дифференциального уравнения определяет в плоскости XOY семейство интегральных кривых, зависящих от произвольной постоянной С. Частному решению соответствует фиксированная интегральная кривая.

Пример 1.3. Проверить, что функция 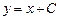есть общее решение дифференциального уравнения 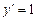и найти частное решение, удовлетворяющее начальному условию . Дать геометрическое истолкование результата.

Решение. Функция 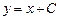удовлетворяет данному дифференциальному уравнению при любых значениях постоянной С, так как .

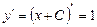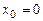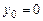Полагая и , получим частное решение 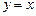. Общее решение 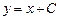определяет в плоскости XOY семейство параллельных наклонных прямых с угловым коэффициентом 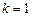, частное решение 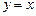определяет наклонную прямую, проходящую через начало координат.

Уравнения с разделяющимися переменными. Дифференциальное уравнение вида

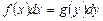
называется уравнением с разделенными переменными.

Уравнение вида:

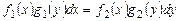
называется уравнением с разделяющимися переменными.

Делением на произведение 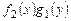оно приводится к уравнению с разделенными переменными

.

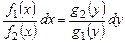Замечание. Деление на произведение 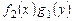может привести к потере частных решений, обращающих в нуль произведение .

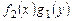Пример 1.4. .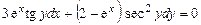

Решение. Разделив обе части уравнения на 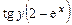, получим

,

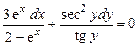уравнение с разделёнными переменными. Интегрируя его, получим

.

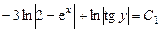После потенцирования получим

.

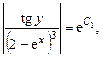
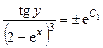Обозначая , будем иметь общий интеграл в таком виде:

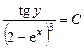, или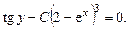

При делении на 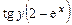могли быть потеряны решения, обращающие в нуль это выражение, именно 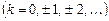и . Непосредственной подстановкой в дифференциальное уравнение убеждаемся, что и являются решениями уравнения.

Окончательный ответ будет таким:

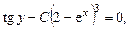
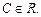
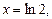
Рассмотрим примеры. (Буква Б перед номерами задач означает, что пример из задачника Бермана.)

Б. 3903. Найти общее решение уравнения:

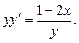
Запишем уравнение в таком виде:

.

Интегрируя, получим общее решение уравнения

, ,

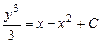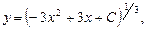
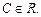
Однородные уравнения. Дифференциальное уравнение 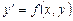называется однородным, если его можно представить в виде

.

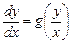Вводя новую переменную 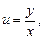имеем ,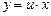

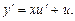
В уравнении можно разделить переменные:

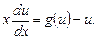
Пример 1.5. .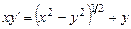

Решение. Пусть , или 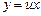, Тогда 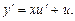Подставляя в уравнение 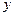и 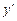, получим

.

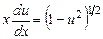Разделив переменные, проинтегрируем

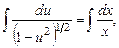
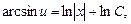или ,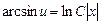

а так как 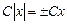, то, обозначая 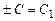, получаем

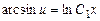, где .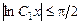

После обратной замены переменных получим

или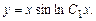

При разделении переменных имело место деление на выражение 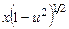, что могло привести к потере решений, обращающих в нуль это выражение. Здесь 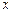- независимая переменная, а из 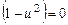следует 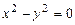, откуда 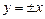. Проверкой убеждаемся, что функци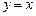и и 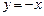также являются решениями дифферен-циального уравнения, поэтому общее решение:

, , .

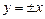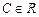Б. 3935. Найти общее решение уравнения .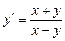

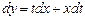Это уравнение является однородным. Положим , тогда . Подставив 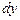в уравнение, получим

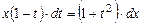
Это - уравнение с разделяющимися переменными. После простых преобразований имеем:

.

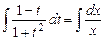В результате интегрирования

.

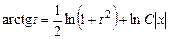Возвращаясь к старым переменным, находим

, C > 0.

Б. 3937.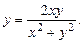

Это - однородное уравнение. Замена переменных 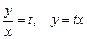, позволит разделить переменные

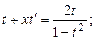
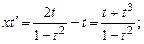
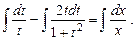
(В числителе первого интеграла прибавили и вычли 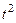и разделили почленно.) После интегрирования имеем:

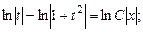
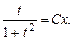
Возвращаясь к старым переменным, получим

.

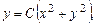
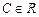Дифференциальное уравнение следующего вида:

,

где 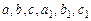- постоянные, а - непрерывная функция, может быть приведено к однородному. Если 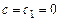, то уравнение является однородным и интегрируется, как рассмотрено ранее.

Если же хотя бы одно из чисел 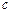или 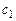отлично от нуля, то дифференциальное уравнение приводится к однородному подстановкой

,

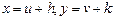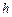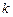где и - решения системы уравнений

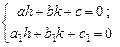при .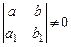

Если же определитель системы равен нулю, то коэффициенты при неизвестных 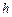и 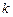пропорциональны

и дифференциальное уравнение имеет вид

.

Подстановка 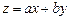приводит его к уравнению с разделяющимися переменными.

Пример 1.6. .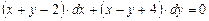

Решение. Рассмотрим систему линейных уравнений:

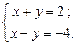Определитель системы: .

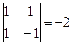Решение системы: 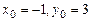. Замена переменных 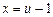, приводит дифференциальное уравнение к виду

.

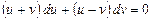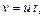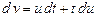Уравнение - однородное. Пусть тогда и

,

откуда следует:

.

Разделим переменные:

.

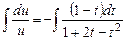Интегрируя, получим

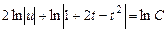или .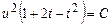

Подставив в последнее выражение 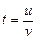, имеем:

.

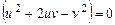Возвратившись к исходным переменным 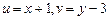; получим:

.

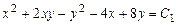
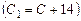Пример 1.7. .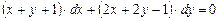

Решение. Система линейных алгебраических уравнений

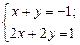
несовместна. Применим подстановку 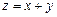, тогда 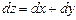и уравнение примет вид

.

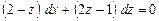После разделения переменных:

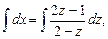
откуда

,

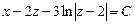и, после перехода к исходным переменным,

, .

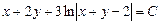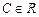2. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА. УРАВНЕНИЕ БЕРНУЛЛИ

Линейным дифференциальным уравнением первого порядка назы-вается уравнение, линейное относительно неизвестной функции и её производной первого порядка 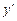. Оно имеет вид:

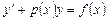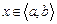, , (2.1)

где 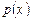и 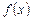- известные функции независимой переменной 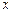, непрерывные на промежутке .

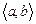Если 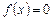, то уравнение (2.1) называется линейным однородным, исходное же уравнение (2.1) с правой частью 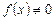называется линейным неоднородным дифференциальным уравнением. Однородное уравнение является уравнением с разделяющимися переменными и имеет общее решение такого вида:

.

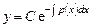Общее решение неоднородного уравнения можно найти методом вариации произвольной постоянной, который состоит в том, что реше-ние ищется в виде

, (2.2)

где 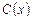- неизвестная функция от 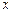. В результате подстановки (2.2) в уравнение (2.1) получаем дифференциальное уравнение, интегрируя которое, удаётся найти функцию .

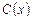Дата добавления: 2015-06-04