Пример 2.1

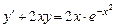. (2.3)

Решение. Однородное уравнение, соответствующее данному неоднородному, имеет вид: 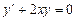, его общее решение , .

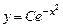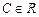Общее решение уравнения (2.3) ищем в виде

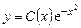, (2.4)

где 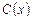- неизвестная функция. Подставляя (2.4) в (2.3), получаем уравнение 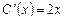, откуда .

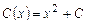В итоге общее решение уравнения (2.3) .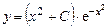

Может оказаться, что дифференциальное уравнение линейно относительно 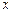как функции независимой переменной 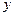, т.е. имеет такой вид:

.

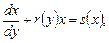
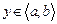Пример 2.2. .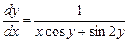

Решение. Данное уравнение является линейным относительно функции 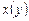и её первой производной:

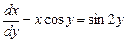. (2.5)

Сначала решаем соответствующее однородное уравнение

.

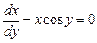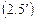
Его общее решение имеет вид 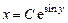, 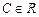. Решение уравне-ния (2.5) ищем в виде

, (2.6)

где 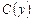- неизвестная функция. Подставляя (2.6) в (2.5), имеем:

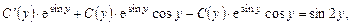
откуда

.

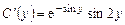Интегрируя по частям, получим:

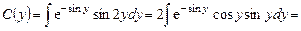
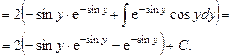
В итоге:

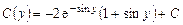. (2.7)

Подставляя (2.7) в (2.6), получаем общее решение исходного дифференциального уравнения:

.

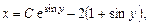
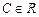Метод вариации произвольной постоянной можно представить себе иначе. Пусть надо решить уравнение следующего вида:

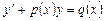. (2.8)

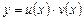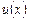Полагаем , где и 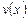- неизвестные функции, одна из которых может быть выбрана произвольно. Если

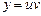, то .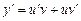

Подставив последние выражения в (2.8), получим:

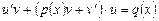. (2.9)

В качестве 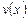можно взять любое частное решение уравнения , не равное нулю. Затем из (2.9) найдём функцию 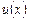, а следовательно, и решение уравнения (2.8), равное .

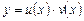Пример 2.3. Решить задачу Коши:

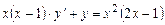(2.10)

.

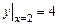Решение. Ищем решение уравнения (2.10) в виде 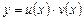; тогда 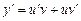и, после подстановк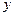и и 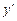в (2.10), получим:

,

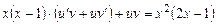или

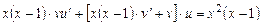. (2.11)

Функцию 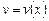находим из уравнения 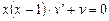, которое получено в результате приравнивания нулю содержимого квадратных скобок в (2.11).

После алгебраических преобразований в последнем уравнении получим уравнение с разделёнными переменными

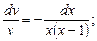частное решение его - .

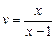Подставив 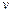в уравнение (2.11), получаем уравнение 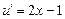, из которого находим 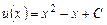. Общее решение уравнения (2.10) будет иметь вид:

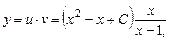, или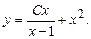

Из начального условия получаем для нахождения C уравнение 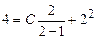, откуда .

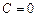В итоге решение задачи Коши: .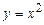

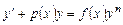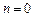Уравнение Бернулли имеет вид . При и 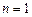оно является линейным, при других значениях 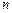приводится к линейному виду с помощью замены переменной .

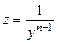Пример 2.4. Решить уравнение

. (2.12)

Решение. Разделив обе части уравнения на 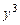; получим

.

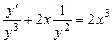При этом следует учесть, что 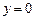является частным решением исходного уравнения.

Сделав замену переменных 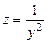, заметим, что 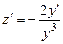. В результате уравнение (2.12) будет преобразовано к виду

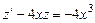. (2.13)

Решая однородное уравнение 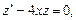находим

.

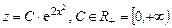Подставив 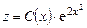в (2.13), получим ,

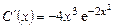откуда:

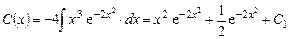и

Общее решение исходного уравнения:

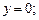
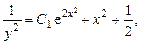
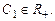
Б. 3957.

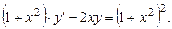
Решение. Разделим на 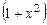левую и правую части уравнения. Поскольку 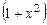не обращается в нуль нигде на оси ОX, никакие решения уравнения потеряны не будут. Получим:

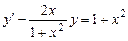. (2.14)

Однородное уравнение, соответствующее данному неоднородному:

.

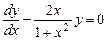Проинтегрируем, предварительно разделив переменные:

.

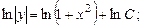
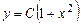Общее решение уравнения (2.14) ищем методом вариации постоянной, подставив в (2.14)

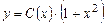, (2.15)

где C(x) - неизвестная функция, получим:

,

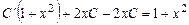откуда

; .

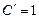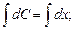
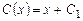Подставив 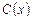в (2.15), получим общее решение исходного дифферен-циального уравнения:

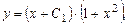
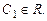
Б. 3961. .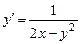

Решение. Это уравнение становится линейным, если 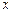считать функцией независимой переменной 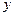. Тогда уравнение примет вид:

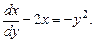(2.16)

Интегрируя соответствующее однородное уравнение, получаем:

.

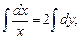
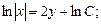
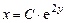Решение уравнения (2.16) ищем в виде

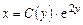. (2.17)

Подставив (2.17) в (2.16), получим:

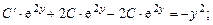
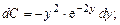
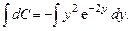
Интегрируя по частям, имеем:

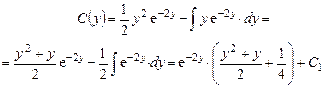
Зная 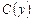, находим общее решение исходного дифференциального уравнения:

.

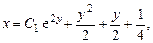
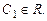Дата добавления: 2015-06-04