Лекція 6

Рівняння неперервності. Закони збереження імовірності, маси, заряду і числа частинок у нерелятивістській квантовій механіці

Розглянемо рівняння Шредінґера

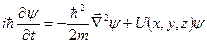. (6.1)

і рівняння комплексно спряжене до нього

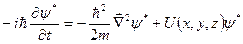. (6.2)

Після множення лівої та правої частин першого рівняння на 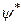, а другого – на 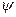, і віднімаємо одне від іншого, отримаємо

. (6.3)

Неважко переконатися, що

. (6.4)

З урахуванням цього отримуємо:

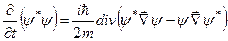. (6.5)

Але є густиною імовірності. Якщо ввести вектор

, (6.6)

тоді густина і вектор 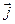будуть задовольняти рівняння

. (6.7)

Якщо 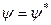, тобто якщо 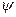є дійсною функцією, тоді вектор 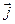=0. Зобразимо хвильову функцію у вигляді комплексної величини в показниковій формі:

, (6.8)

де – фаза комплекснозначної функції 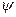. Тоді

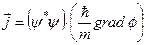, (6.9)

або

, де швидкість . (6.10)

Приклад: Хвильова функція вільної частинки, яка рухається з імпульсом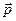

. (6.11)

У цьому випадку 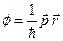, а 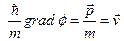. Отже, вектор 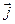є густиною потоку імовірності, а рівняння

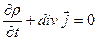(6.12)

є рівнянням неперервності. Величину 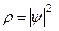можна розглядати як середню густину числа частинок; тоді 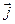має зміст середнього потоку частинок через одиницю поверхні за одиницю часу. Рівняння неперервності формулює закон зберігання числа частинок у нерелятивістській квантовій механіці. Дійсно, ін­тегруючи рівняння неперервності за фіксованим об’ємом V простору, отри­муємо

. (6.13)

За допомогою формули Остроградського-Ґауса перетворимо об’ємний інтеграл від дивергенції у поверхневий

, (6.14)

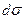де – замкнута поверхня, що обмежує об’єм V, а – „елемент поверхні”, , – зовнішня нормаль до . Поширюючи інтегрування на весь прос­тір (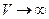) і застосовуючи граничну умову обернення 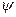в нуль на нескінчен­ності, отримаємо відомий закон збереження імовірності в інтегральній формі

, (6.15)

тобто повна імовірність знайти частинку де-небудь у просторі не змінюється з часом t.

Запишемо рівняння неперервності для маси та заряду. Введемо середню густину маси 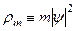, де m – маса частинки, та середню густину потоку ма­си

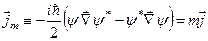. (6.16)

Тоді матимемо

. (6.17)

Введемо середню густину заряду , де e – заряд частинки, та серед­ню густину електричного струму 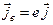і одержимо закон збереження заряду

. (6.18)

Висновок. У класичній фізиці при розгляді руху контину­уму одна­кових частинок (суцільного середовища) одержимо класичне рівняння неперерв­ності. В електродинаміці з рівнянь Максвелла отримаємо рівняння неперерв­ності для густини заряду і струму. У квантовій механіці з хвильового рівняння Шредін­ґера одер­жимо рівняння неперервності. Це рівняння виражає два закони нереляти­вістсь­­кої квантової механіки: закон збережен­ня густини імовірності числа частинок і закон збе­реження заряду. Має місце також неперервність потоку 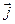, і, як буде показано, неперервність хвильових функцій та їх перших похідних.

Оператор похідної за часом від оператора (означення). Зміна середніх значень фізичних величин з часом. Інтеграли руху. Теорема Еренфеста.

Означення. Оператор похідної за часом від оператора – це такий оператор , який визначається рівністю

. (6.19)

Тут 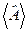– середнє значення фізичної величини A, якій відповідає оператор , отже,

. (6.20)

Розглянемо тепер зміну цього середнього значення в довільному стані 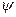із часом. Знайдемо похідну

. (6.21)

Підставимо з рівняння Шредінґера значення похідних

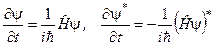(6.22)

і, скористаємось ермітовістю оператора 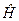, одержимо

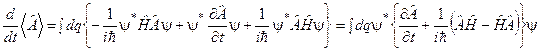. (6.23)

Отже, згідно означення оператора похідної від оператора

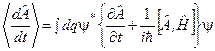, (6.24)

тобто середнє значення уведеного оператора дорівнює середньому зна­чен­ню від величини, якій відповідає оператор 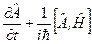. Таким чином, маємо

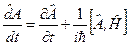. (6.25)

Згадаємо означення квантових дужок Пуассона і перепишемо вираз для оператора у вигляді

. (6.26)

Означення: Фізична величина A є інтегралом руху, якщо 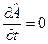і 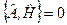. Такі фізичні величини зберігаються з часом:

, за t. (6.27)

Як слідує з означення, для того, щоб величина A була інтегралом руху, опе­ратор цієї величини повинен комутувати з оператором Ґамільтона

. (6.28)

Твердження: якщо два оператори комутують між собою, тоді вони мають спіль­ну систему власних функцій, відповідні фізичні величини можуть бути одночасно виміряні. Доведемо це.

Нехай , 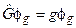. Система функцій 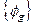є повною. Це означає, що функцію 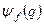можна розкласти в ряд

. (6.29)

Візьмемо довільну функцію від оператора і розглянемо оператор , де 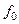– довільна функція. Подіємо цим оператором на розклад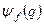

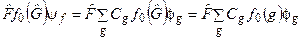. (6.30)

З іншого боку, подіємо на цей розклад оператором :

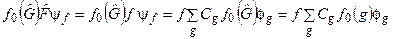. (6.31)

Але оператори 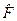і комутують між собою, це означає, що і комутатор

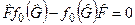. (6.32)

Отже, вирази і рівні між собою. З цього випливає, що

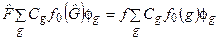(6.33)

або

. (6.34)

Внаслідок довільності функції остання рівність виконується при умові, що

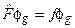, (6.35)

тобто 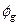є також власною функцією оператора .

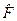Висновок: якщо оператори 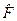та комутують, то вони мають спільну систему власних функцій. Зручно позначати цю спільну систему власних функ­цій символом 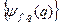. У станах, які описуються цими хвильовими функціями, фі­зичні величини F і G мають точні значення f і g. Ці значення можуть бути вимі­ряними одночасно.

Отже, інтеграли руху вимірюються одночасно з енергією системи, оскільки оператори, які відповідають інтегралам руху, повинні комутувати з оператором Ґамільтона (див. означення інтеграла руху).

Приклад („воднева” задача для практичних занять): електрон рухається у центрально-симетричному кулонівському полі ядра із зарядом 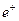. Враховуючи той факт, що відношення маси електрона m до маси ядра M є малою величиною (m / M <<1), будемо вважати ядро „нерухомим” і помістимо його у початок координат. Ґамільтоніан такої системи має вигляд

, (6.36)

де 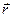– радіус-вектор електрона, .

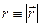Довести, що три оператори, а саме, Ґамільтоніан системи 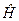, оператор квад-рата моменту кількості руху 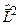, 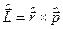і оператор проекції 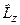моменту кіль­кості руху, комутують між собою.

Висновки: 1) У водневій задачі три фізичні величини – повна енергія E, квадрат моменту кількості руху L ² і проекція L_z, є інтегралами руху. 2) Операто­ри 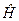, 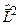і 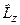мають спільну систему власних функцій. Отже, три фізичні вели­чи­ни E, L ² і L_z, що відповідають цим трьом операторам, можуть бути одночасно виміряні.

Відмітимо, що відповіді на сформульовані вище питання водневої задачі є ду­же важливими. Саме на них ми будемо спиратися при знаходженні виразів для хвильових функцій і енергій електрона, який рухається в полі кулонівсько­го потенціалу, що й завершить розв’язок квантово-механічної проблеми Кепле­ра.

Теорема Еренфеста. Застосуємо отримані вище співвідношення до імпульсу і координати. Для простоти розглянемо одновимірний рух вздовж осі x. Імпульс 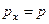і координата x не залежать явно від часу, тому оператори похідних від опе­раторів 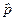і 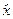мають вигляд

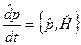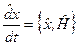, , (6.37)

де

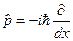, . (6.38)

Аналогом цих рівнянь у класичній механіці є рівняння Ґамільтона для частин­ки, яка рухається в потенціальному полі 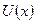, записані через класичні дужки Пуассо­на

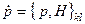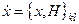, , (6.39)

Виконаємо обчислення:

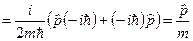. (6.40)

, (6.41)

. (6.42)

Отже,

, , (6.43)

Система операторних рівнянь (6.43) є аналогом рівнянь Ґамільтона у кла­сич­ній механіці. Візьмемо від обох частин першого з рівнянь (6.43) похідну за часом

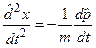, (6.44)

і, скористаємось другим рівнянням, тоді одержимо

. (6.45)

З цього операторного рівняння слідує вираз для середніх значень

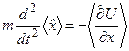. (6.46)

По вигляду це рівняння нагадує рівняння Ньютона з класичної механіки, але во­но записане для середніх значень відповідних величин. Співвідношення між се­редні­ми значеннями величин у квантовій механіці мають таку саму форму, як і відпо­відні співвідношення між величинами у класичній механіці. Всі ці рівнян­ня складають зміст так званої теореми Еренфеста: квантові рівняння руху для операторів (або, як ще кажуть, рівняння руху в формі Ґейзенберга) отри­мують­ся з класичних рівнянь формальною заміною фізичних величин відповід­ни­ми операторами або класичних дужок Пуассона – відповідними кванто­вими дужками Пуассона.

Дата добавления: 2015-06-04