Лекція 4

Приклади квантовомеханічних фізичних величин у координатному зображенні. Квантові дужки Пуассона

Вище ми ввели оператори проекції координат та імпульсу. Вони є самоспря­женими розв’язками комутативних співвідношень Ґейзенберга. Для введен­ня опе­раторів інших фізичних величин, слід використати класичні означення цих ве­личин. Ознайомимося з поняттям „функції від оператора” 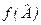. Під функ­цією 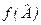розуміємо розклад функції 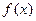у ряд Тейлора за степенями 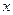із заміною 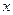на :

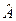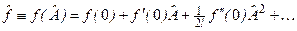(4.1)

Легко збагнути, що слід розуміти під функцією 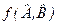, якщо самоспряжені опе­ратори 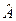і 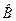комутують (тобто, 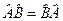). Але немає загального правила згаданого зіставлення в тому випадку, коли оператори 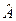і 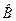не комутують. Зате існує, так зване, правило Вейля, але й тут питання про однозначність зіставлення оператора з будь-якого функцією фізичних величин залишається відкритим.

Приклади операторів квантової механіки наведено в таблиці:

Фізична величина	Оператор
Координата: 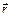; 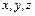.	Оператор множення: ; .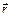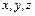
Імпульс: ; .	; , , .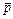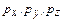
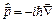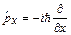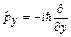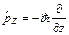Кінетична енергія:	, .
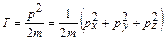
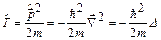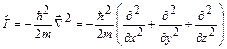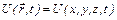
Потенціальна енергія:	Оператор множення: , .
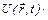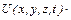Повна енергія (нерелятивістське наближення): 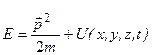.	Оператор Ґамільтона (Ґамільтоніан): .
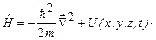Момент кількості руху: , , , .	, , , .

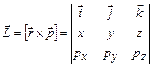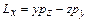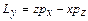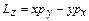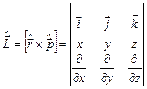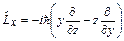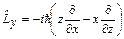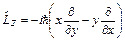Тепер ми розглянемо декілька прикладів на комутацію операторів квантової механіки і познайомимося з квантовими дужками Пуассона. Ми побачимо ана­логію квантових дужок Пуассона з відповідними співвідношеннями у класичній механіці.

Ми уже знаємо, що у квантовій механіці мають місце такі комутаційні спів­відношення:

,

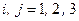, . (4.2)

Легко одержати також комутаційні співвідношення для операторів проекцій моменту кількості руху 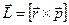(див. математичний додаток до лекцій):

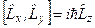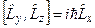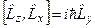, , . (4.3)

Введемо тепер такий ермітовий оператор

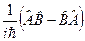. (4.4)

Цей оператор позначають символом 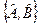і називають квантовими дужками Пуассона операторів 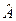і 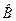. Ці дужки Пуассона, як виявляється, мають анало­гію з класичними дужками Пуассона у механіці. Дійсно, адже

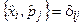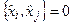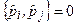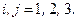, , , (4.5)

Крім того,

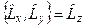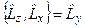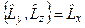, , . (4.6)

Ці операторні співвідношення нагадують класичні дужки Пуассона для ка­нонічно спряжених змінних класичної механіки (так звані фундаментальні кла­сичні дужки Пуассона), а також класичні дужки Пуассона для проекцій момен­ту руху у механіці.

Наведемо ще один яскравий приклад вищезгаданої аналогії: легко перекона­тися, що для будь-якої функції 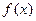має місце співвідношення

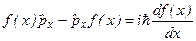, (4.7)

або

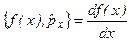. (4.8)

Наведемо тепер п’ять характерних прикладів для операторів Ґамільтона і п’ять прикладів для рівнянь на власні значення та власні функції цих операто­рів.

Приклад 1. Частинка, маси 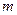рухається в одновимірній прямокутній потен­ціальній ямі (див. рис. 4.1):

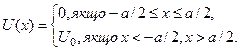(4.9)

Рис. 4.1. Потенціальна енергія прямокутної форми.

Тут 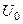та 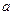– розміри ями, 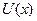– потенціальна енергія частинки. Оператор Ґамільтона у цьому випадку матиме вигляд

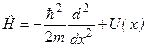, (4.10)

а рівняння на власні значення 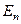і власні функції 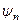цього оператора зводиться до такого рівняння:

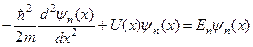. (4.11)

Простішим є випадок безмежно високих потенціальних стінок (). У цьому випадку рух частинки буде відбуватися тільки в обмеженій області (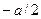, 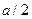). Згідно загальним міркуванням гранична умова в точках 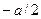і 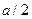зводиться до 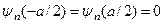. Корисно буде розв’язати цю задачу на прак­тичних заняттях і при цьому одержати таку відповідь^*):

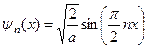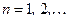, , (4.12)

Приклад 2. Гармонічний осцилятор.

У класичній механіці гармонічним осцилятором називаємо механічну систе­му, у якої функція Ґамільтона має вигляд:

. (4.13)

Якщо замінити у виразі для 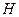класичні величини 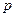і 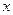відповідними опе­рато­рами в координатному зображенні, тоді одержимо оператор Ґамільтона (Ґамільтоніан) гармонічного осцилятора у квантовій механіці:

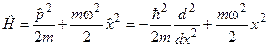. (4.14)

Тепер рівняння на власні значення 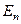і власні функції 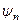гармонічного осцилятора матиме вигляд:

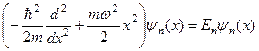. (4.15)

Розв’язок цього рівняння дає рівні енергії 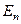і хвильові функції 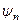гармо­нічного осцилятора. Ми тут напишемо цей розв’язок:

,

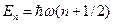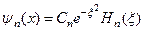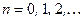, (4.16)

Сталі 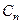знаходять з умови нормування хвильових функцій 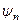, тобто з умо­ви, що

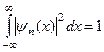. (4.17)

Звідси одержують, що

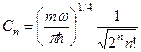. (4.18)

У виразі для хвильових функцій 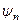використано позначення 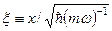, а 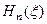– це відомий поліном Ерміта.

Як бачимо (див. рис. 4.2), рівні енергії є еквідистантними

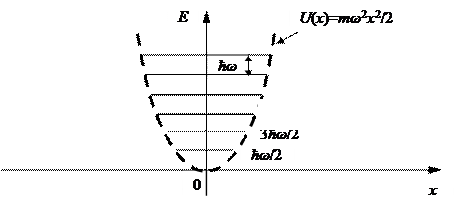Рис. 4.2. Рівні енергії лінійного гармонічного осцилятора. Графік функції .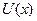

Зауважимо, що модель лінійного гармонічного осцилятора у багатьох проблемах є добрим наближенням до реальної атомної чи молекулярної систе­ми.

Приклад 3. Оператор проекції моменту кількості руху .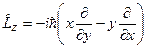

Якщо аргументом хвильової функції 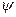є не декартові координати 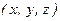, а сферичні 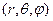, тоді необхідно відомим чином замінити змінні, а саме, 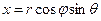, , 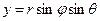, 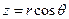і перейти за загальним правилом від операторів 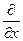, , 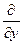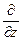до операторів 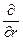, , 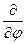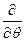. Зокрема, маємо:

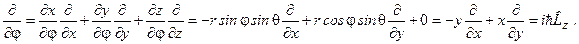
(4.19)

Отже, 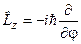. Тепер рівняння на власні значення та власні функції цього оператора у сферичних координатах має вигляд:

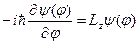. (4.20)

Тут азимутальний кут 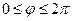, а розв’язок 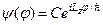. Власні значення 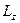знаходимо з умови однозначності хвильової функції :

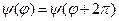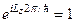, або 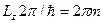, 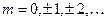(4.21)

Отже, 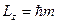. Для знаходження сталої 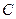запишемо умову нормування хви­льової функції :

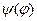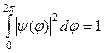. (4.22)

З цієї умови визначаємо 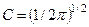. Остаточно, власні функції оператора проекції моменту кількості руху мають вигляд:

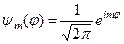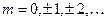, (4.23)

Приклад 4. Атом водню (електрон у кулонівському полі).

Йдеться про рух електрона у полі „нерухомого” ядра. Нехай заряд ядра до­рівнює 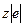. Потенціальна енергія взаємодії електрона і ядра

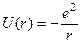(4.24)

залежить лише від модуля радіус-вектора електрона 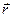, 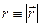. Тоді оператор Ґамільтона для однієї частинки (електрона) маси 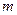з координатою 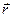, що рухаєть­ся у полі 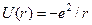, матиме вигляд:

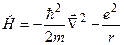. (4.25)

Власні значення 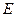і власні функції 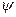цього Ґамільтоніана – це розв’язки та­кого рівняння:

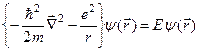, (4.26)

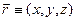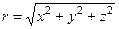, . Внаслідок сферичної симетрії потенціалу для успішного розв’язання цього рівняння зручно перейти до сферичних координат 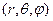за відомими правилами. Ці нескладні, але доволі громіздкі розрахунки ми зробимо іншим разом. Скажемо тільки, що знання власних значень операто­ра енергії та його власних функцій дасть нам теорію атома водню (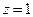) та водневоподібних систем, таких як іон гелію (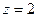), подвійний іон літію (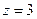) і т.д. Рівні енергії дискретного спектра водню визначаються формулою

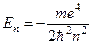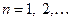, (4.27)

Це є знаменита формула Н. Бора.

Приклад 5. Система двох електронів у полі „нерухомого” атомного ядра із зарядом 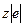(див. рис. 4.3).

До таких систем належать атом гелію, однократно іонізований атом літію, від’ємний іон водню та інші багатократні іони.

	1-й електрон

z

Рис. 4.3. Система двох електронів у (зовнішньому) кулонівському полі „нерухомого” ядра.

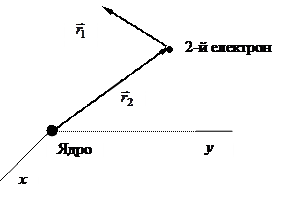
Запишемо Ґамільтоніан такої системи, помістивши ядро в початок коорди­нат. Якщо скористатися позначеннями 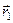, 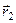– радіус-вектори електронів, 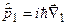, 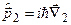– оператори їхніх імпульсів, , , 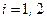а 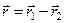, тоді наш Ґамільтоніан запишеться у вигляді:

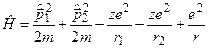, (4.28)

або

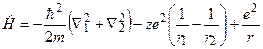. (4.29)

Тут 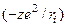, , 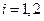є оператор енергії взаємодії i -того електрона з ядром, а 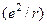– оператор енергії міжелектронної взаємодії. Хвильова функція тут зале­жатиме від шістьох декартових координат .

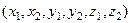Зробимо тепер одне важливе зауваження: у деяких випадках при знаход­женні розв’язків рівняння на власні значення і власні хвильові функції (у мате­матиці таку задачу називають задачею Штурма-Ліувілля) одному й тому влас­ному значенню 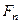відповідає не одна, а більше хвильових функцій 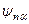, 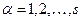. Тоді говорять, що власне значення 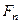є виродженим s -кратно. Число може бути й безмежним, тобто маємо безмежно-кратне виродження, що мож­на проілюструвати на такому прикладі:

Власне значення і власна функція оператора імпульсу в координатному зображенні

Легко переконатися, що власною функцією оператора імпульсу 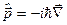є плоска хвиля де Бройля

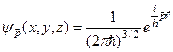. (4.30)

Справді, після безпосередньої дії на цю функцію оператора імпульсу 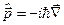маємо:

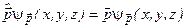. (4.31)

Ця функція 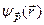є також власною функцією і оператора кінетичної енергії :

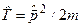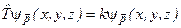. (4.32)

Тут власне значення кінетичної енергії 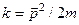, яке не залежить від на­прямку імпульсу 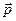, . Маємо приклад безмежнократного виродження, значенню 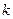відповідає безліч функцій 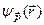з різними напрямками вектора .

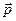Дата добавления: 2015-06-04