Лекція 3

Математичний апарат квантової механіки

При побудові математичного апарату квантової механіки будемо спиратися на результати двох експериментів, а саме: дифракція електронів та про­ходження „поодинокими” електронами (фотонами) крізь екран з щілинами. У пер­шому з дослідів була підтверджена гіпотеза Л. де Бройля про те, що з частин­кою пов’язаний хвильовий процес, який характеризується довжиною хвилі 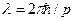(тут р є імпульсом частинки, тобто її корпускулярною характер­ристикою), у другому – експериментально встановлене співвідношення не­визна­ченостей Ґейзенберга, про що йшлося у Лекції 1. Щоб ці експерименти знайшли своє послідовне теоретичне обґрунтування у квантовій механіці, поряд з наявною вже у Лекції 2 аксіомою про простір фізичних станів квантової системи, потрібно запропонувати ще й цілу низку нових аксіом. Система всіх цих аксіом складатиме фундамент квантової механіки. Перевіркою достовірності цього фундаменту, його відпо­відності природі мікросвіту є співставлення висновків і наслідків квантової теорії з експериментом.

У квантовій механіці, як буде показано нижче, спостережувані величини представлені лінійними самоспряженими операторами, які діють у просторі хвильових функцій . Спостережувані фізичні величини – це ті величини (наприклад, положен­ня 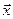, імпульс 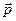, енергія E, момент імпульсу 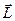, тощо), які характеризують квантову систему і вимірюються експериментально. З матема­тичної точки зору, квантова механіка – це теорія лінійних операторів.

Оператори фізичних величин, операція усереднення у стані . Оператор 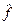вважають визначеним на деякій множині функцій , якщо вказано закон („рецепт”), за яким кожній функції із множини ставиться у відповідність функція φ, яка теж належить цій же множині функцій:

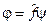. (3.1)

Приклад 1. Оператори 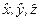– це оператори множення на незалежну змінну:

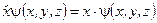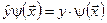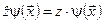; ; . (3.2)

Приклад 2. Оператори 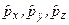зводяться до диференціювання функції 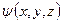і множення відповідних частинних похідних на постійну величину (– iħ):

,

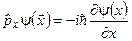, (3.3)

.

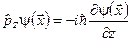Введемо позначення < F > або 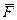для середнього значення фізичної величини F. Знайдемо середнє значення радіуса-вектора електрона в стані . Як відо­мо, густина імовірності певних значень радіуса-вектора задається через функ­цію стану :

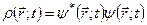, (3.4)

отже, згідно з поняттям „математичне очікування”, середнє значення 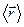радіус-вектора електрона у стані визначається інтегралом:

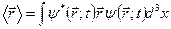. (3.5)

Аналогічно визначається середнє значення фізичної величини F у стані , коли F є довільною функцією положення електрона:

. (3.6)

У всіх наведених виразах час t фіксований. У квантовій механіці правило (3.6) узагальнюється на випадок знаходження середнього значення будь-яких фізичних величин. Для цього вводиться спеціальна математич­на операція усе­ред­нення у стані , яку також позначають через кутові дужки

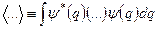, (3.7)

де q – сукупність змінних, від яких залежить хвильова функція.

Аксіома (постулат) про спостережувані: кожній фізичній величині F у кван­товій механіці ставиться у відповідність оператор цієї величини 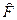такий, що середнє значення величини F у стані дорівнює

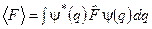. (3.8)

Очевидно, оператор 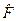визначений на множині хвильових функцій. Зіставлення операторів з фізичними величинами повинно узгоджуватися, як із принципами квантової механіки, так із тим, що фізичні величини спостерігаються на експе­ри­менті:

а) Принцип суперпозиції вимагає, щоб оператори фізичних величин були лінійними операторами, тобто

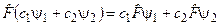. (3.9)

б) Середні значення фізичних величин є дійсними, тобто

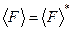. (3.10)

В інтегральній формі ця вимога може бути записана у вигляді:

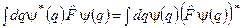. (3.11)

Скалярний добуток векторів простору L ₂. Комплексне число

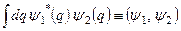(3.12)

за означенням є скалярним добутком вектора 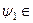L ₂ на вектор 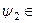L ₂; тут 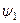і 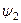– довільно фіксовані вектори із простору фізичних станів квантової системи, тобто із простору L ₂.

Спряжений та самоспряжений оператори в L ₂. Лінійний оператор 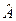, який діє у просторі L ₂, має також т. з. спряжений оператор 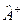. Якщо оператор 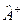є спряженим до оператора 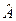, тоді він неодмінно (за означенням) має задовольня­ти рівність

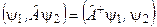(3.13)

при всіх тих векторах 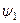, 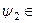L ₂, для яких є визначеними ліва та права сторони рівності (3.13).

Лінійний оператор 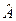в Ґільбертовому просторі має назву самоспряженого (ермітового) оператора, якщо

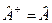. (3.14)

Цю рівність можна представляти у двох еквівалентних формах:

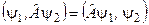(3.15)

або

. (3.16)

Твердження. Якщо оператор 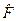самоспряжений (ермітовий), тоді середнє значення фізичної величини F у стані є дійсною величиною.

Доведення: Нехай 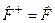. Тоді для будь-якого стану , що належить області визначення оператора 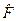, має місце рівність

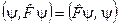. (3.17)

Але з математичної точки зору число 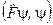є комплексно спряженим до числа 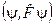. Отже,

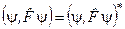. (3.18)

Висновок: всі ті оператори квантової механіки, які згідно з аксіомою, співставляються спостережуваним на експериментах фізичним величинам є лінійними самоспряженими (ермітовими)операторами.

Введемо в розгляд два оператори, які знадобляться нам у майбутньому: оператор відхилення та оператор середньоквадратичного відхилення. Значен­ня, яке можемо одержати при вимірюванні деякої фізичної величини 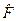у стані позна­чимо через F. У кожному акті вимірювання матимемо відхилення зна­чення F від < F>. Для розрахунку середньоквадратичного відхилення значень F від значення < F> введемо оператор :

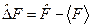. (3.19)

Очевидно, що середньоквадратичне відхилення рівне

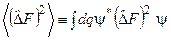. (3.20)

Оператор положення та оператор імпульсу мікрочастинки у квантовій механіці. Розглянемо питання про те, як слід задавати оператори положення 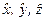та імпульсу 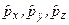мікрочастинки.

Теорема. Для того, щоб мали місце співвідношення невизначеностей Ґейзенберга, необхідно й достатньо, щоб оператори 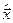і 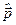були самоспряженими розв’язками таких операторних рівнянь:

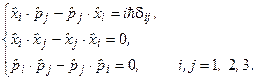(3.21)

Оператор 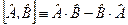має назву комутативного співвідношення опера­торів 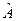і 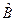. Якщо 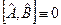, тоді кажуть, що оператори 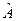і 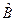комуту­ють. Комутаційні співвідношення (3.21) називають комутативними співвід­ношення­ми Ґейзенберга. Доведення теореми за браком місця нами опущено – його можна знайти в стандартних підручниках з квантової механіки. Натомість проаналізуємо одне важливе для формалізму квантової механіки твердження:

Якщо оператори 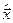і 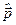є самоспряженими розв’язками комутативних співвідношень Ґейзенберга, тоді і оператори 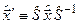і 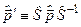також є само­спряженими розв’язками ґейзенбергових комутативних співвідношень. Тут 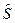довільно фіксований несингулярний оператор, тобто такий, для якого існує обернений оператор 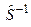, який, за означенням, задовольняє умові

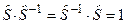. (3.22)

Довести справедливість цього твердження легко, адже

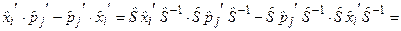
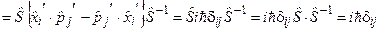. (3.23)

Як видно, досить знайти один самоспряжений розв’язок комутативних співвідношень Ґейзенберга, як інші розв’язки („штриховані”) і 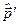цих спів­відношень будуть визначатися вибором оператора 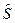. Отже, штрихованих само­спряжених розв’язків співвідношень (3.21) може бути багато.

Координатне та імпульсне зображення операторів та хвильових функцій у квантовій механіці

Легко переконатися, що оператор 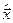множення на незалеж­ну змінну 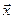та оператор 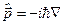є самоспряженими розв’язками комутативних співвідношень. Доведення цього факту виноситься на практичні заняття.

Щойно вибране зображення самоспряжених операторів 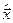і 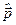справедливе для випадку, коли вони діють на хвильові функції як функції просторових координат, тобто 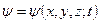, t – параметр. Крім того, у цьому зображенні опе­ратор координат 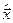зводиться до множення на незалежну змінну :

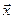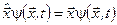, (3.24)

а хвильові функції залежать тільки від координат 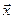. Подібне зображення має назву власного зображення оператора координати, або, коротко, координат­ного зображення операторів та хвильових функцій*⁾.

В імпульсному*⁾ зображенні хвильових функцій останні залежать тільки від імпульсів 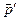, а оператори та 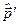мають вигляд:

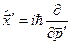, , (3.25)

тобто,

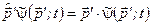, (3.26)

Надалі штрихи в позначеннях операторів і змінних будемо опускати. Позна­чимо через 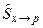оператор, який зв’язує координатне та імпульсне зображення, тоді 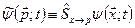. Якщо 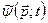є фур’є-компонентою функції 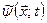, то має місце вираз

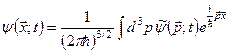. (3.27)

Отже 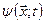та 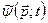– це одна і та ж хвильова функція, але записана один раз в x -зображенні, а другий раз – у p -зображенні. Густина імовірності певних зна­чень імпульсу мікрочастинки у стані 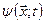виражається уже через функцію

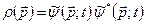. (3.28)

Власні функції і власні значення операторів та їх фізична інтерпретація. Аксіома про спектр значення оператора фізичної величини

Здійснимо вимірювання значення фізичної величини F для деякої квантової системи, стан якої задає хвильова функція . У кожному акті вимірювання зна­чення F, яке ми отримаємо, не збігається з середнім значенням < F >, тобто існують певні відхилення вимірюваних значень від середнього значення.

Задача. Знайти такі стани квантової системи, в яких фізична величина має певне значення F = < F >. Ці стани мають задовільняти рівняння

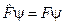. (3.29)

Дійсно, у цьому випадку квадрат норми вектора 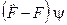рівний нулеві:

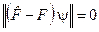, (3.30)

тобто

. (3.31)

Тут 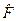– самоспряжений оператор, F – дійсна величина, отже, різниця 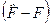є також самоспряженим оператором, який діє на хвильові функції. Властивість самоспряженості оператора 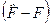та рівність нулеві норми вектора 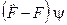приводять до таких рівностей

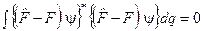, (3.32)

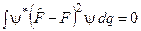, (3.33)

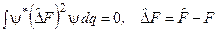. (3.34)

Але 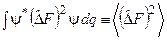– середньоквадратичне відхилення F від < F > у стані .

Висновок. У стані квантової системи, який задовольняє рівнянню 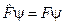маємо, що F = < F >.

У загальному випадку рівняння 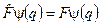є лінійним однорідним дифе­ренціальним рівнянням у частинних похідних. Розв’язуючи це рівняння, шука­ють функцію і відповідне число F, які задовольняють це рівняння. Такі дифе­ренціальні рівняння, як відомо, мають розв’язки не для довільних значеннях F, а тільки для певного набору F ₁, F ₂, F ₃,... значень цієї величини. F ₁, F ₂, F ₃ називають власними значеннями опе­ратора 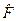. Відповідні цим власним значенням функції ψ ₁, ψ ₂, ψ ₃,... – власними функціями оператора 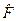. Сукупність власних значень оператора 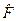є спектр цього оператора. Таким чином, рівняння на власні значення F_n та власні функції 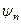можна записати у вигляді

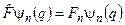. (3.35)

Повернемося до питання вимірювання фізичної величини F. Коли кван­това система перебуває у стані 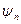, який є власним станом оператора 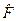, тоді кож­не вимірювання фізичної величини F у цьому власному стані дає тільки одне з можливих зна­чень спектру оператора 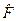, а саме значення F_n. Якщо ж стан не співпадає з власним станом оператора 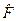, тоді в кожному акті вимірювання ми будемо одержувати вже різні значення величини.

Сформулюємо аксіому стосовно спектру опера­тора фізичної величини. У будь-якому фізичному стані 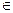L ₂ результатом вимірювання фізичної ве­личини, яка зображається оператором 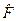, може бути тільки одне зі значень спектру цього оператора. Ні в одному з вимірювань не отримуються значення, які не містяться у спектрі цього оператора .

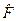Підведемо короткий підсумок: при вимірюванні фізичної величин F у стані квантової системи, кожне окреме з вимірюваннь дає своє, відмінне від інших вимірювань, значення фізичної величини. Це значення неодмінно нале­жатиме спект­ру самоспряженого оператора 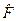. Отже, зміст операторів квантової меха­ніки полягає в тому, що їхні власні значення, що належать спект­ру, співпадають із тими, що вимірю­ються експериментально, коли система перебуває в якомусь довільному стані . Якщо ж стан = 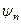є власною функцією оператора 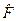, тоді неодмінно кож­не вимірювання фізичної величини F у цьому стані дає одне і те ж значення, яке співпадає з власним значенням F_n оператора .

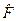Дата добавления: 2015-06-04