Лекція 7

Математичні додатки до практичних занять

1) Вирази для оператора моменту кількості руху 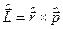у сферичній системі координат.

Запишемо пряме і обернене (зворотне) перетворення між декартовими і сфе­рич­ними координатами:

Пряме перетворення:

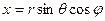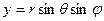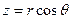, , . (7.1)

Обернене (зворотне) перетворення:

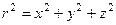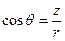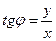, , . (7.2)

Запишемо вирази для похідних:

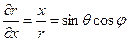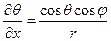, , (7.3)

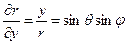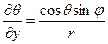, , (7.4)

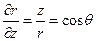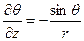, , (7.5)

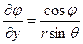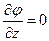, , . (7.6)

Запишемо вирази для операторів 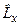, 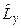і 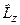у сферичних координатах

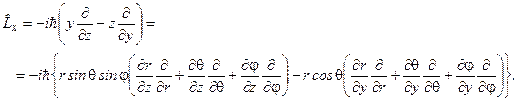
Остаточно

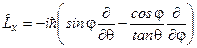. (7.7)

Аналогічно

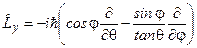, (7.8)

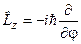. (7.9)

2) Власні значення і власні функції оператора квадрата кутового моменту .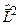

Оператор квадрата моменту кількості руху 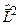має вигляд

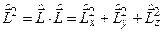. (7.10)

Зручно користуватися цим оператором, якщо записати його вираз через сферич­ні координати 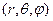. Для цього слід виконати нескладні, але доволі нудні розрахунки. Ці розрахунки ми залишаємо зробити самому студентові. Кожний сту­дент їх виконає без особливих зусиль і одержить:

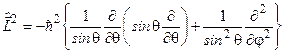. (7.11)

Привертає увагу той факт, що оператори 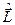і у сферичних координатах міс­тять тільки кутові змінн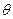і і 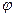та їх похідні.

Для знаходження власних значень і власних функцій оператора квадрата мо­менту кількості руху слід розв’язати диференціальне рівняння

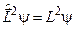. (7.12)

Це рівняння у сферичних координатах зводиться до такого рівняння:

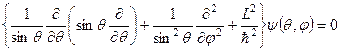. (7.13)

Зрівняємо це рівняння з добре відомим у математиці диференціальним рівнян­ням для т. з. сферичних функцій :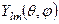

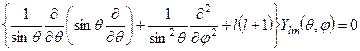, (7.14)

де 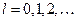Ці рівняння співпадають, якщо

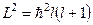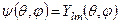, . (7.15)

Квантове число 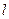є орбітальним квантовим числом. Індекс 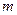сфе­рич­ної функції свідчить про наявність виродження. Число 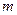має назву магнітного квантового числа. Це число 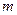при заданному 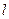приймає значення

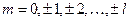, (7.16)

що слідує з рівняння для 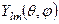. Отже, кожному власному значенню 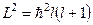, тобто кожному значенню орбі­таль­ного квантового числа 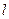, відповідають власні функції .

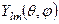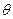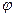Запишемо явну залежність сферичних функцій від кутів і для :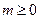

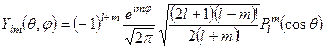, (7.17)

де 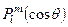є т.з. приєднаний поліном Лежандра

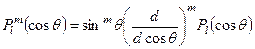, (7.18)

а 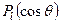є поліном Лежандра

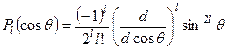. (7.19)

Сферичні функції для від’ємних значень 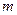визначаються з умови

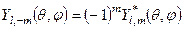. (7.20)

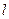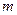Сферичні функції нормовані, а функції з різними квантовими числами і орто­гональні між собою. Умову нормування і ортогональності можна записати у вигляді

, (7.21)

тут , , .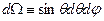

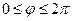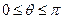Використовуючи явний вигляд сферичних функцій легко переконатися, що ці функції є власними функціями не тільки оператора 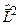, а й оператора проекції 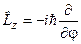цього кутового моменту 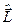на вісь 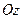. Дійсно, вся залежність функ­цій 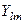від кута 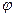зосереджена у співмножнику 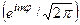, який є не що інше, як власна функція оператора 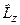з власним значенням 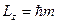. Отже,

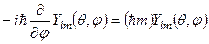. (7.22)

Висновок: оператори 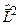і 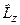комутують, отже мають спільну систему влас­них функцій 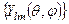. Сферична функція 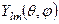є (одночасно) власною функ­цією оператора квадрата моменту імпульсу 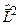, що відповідає власному зна­чен­ню

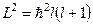, (7.23)

і є власною функцією оператора проекції кутового моменту на вісь 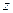з власним значенням .

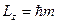3 ) Загальні властивості руху частинки у полі сферичної симетрії (у полі цент­раль­ної сили).

Стаціонарні стани частинки, яка рухається у сферично симетричному полі, описують­ся рівнянням Шредінґера з оператором Ґамільтона, який представляє со­бою суму оператора потенціальної енергії і кінетичної енергії 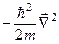час­тин­ки. Запис оператора потенціальної енергії має простий вигляд у тих систе­мах координат, які явно відзеркалюють властивості симетрії квантової системи. У нашому випадку це сферична система координат. 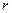У цій системі координат потенціальна енергія є функцією віддалі від центра сили до частинки, тобто 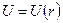. Зручно і оператор кі­нетичної енергії записати теж у сферичній системі координат. Для цього достат­ньо знати вигляд оператора Лапласа 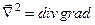у сферичних координа­тах. У курсі „Диференціальна геометрія” відомий загальний вигляд оператора Лапла­са у довільній ортогональні системі координат. Ми запишемо окремі ви­пад­ки цього загального вигляду оператора Лапласа:

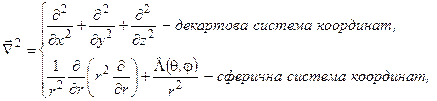(7.24)

де оператор

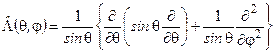. (7.25)

Звідки випливає, по-перше, оператор Ґамільтона 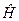для частинки, яка руха­єть­ся у полі сферичної симетрії, і оператор квадрата моменту імпульсу 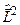у сфе­рич­ній системі координат зв’язані між собою простим співвідношенням

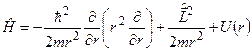, (7.26)

по-друге, це означає, що оператор квадрата кутового моменту у сферичних коорди­натах має вигляд

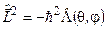(7.27)

і крім того, по-третє, знаємо, що оператор проекції 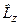моменту 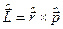на вісь 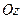має вигляд

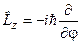. (7.28)

Записані щойно явні вирази для трьох операторів свідчать про те, що опера­тор квадрата кутового моменту 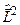і оператор проекції моменту на вісь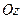 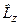кому­тують з оператором Ґамільтона 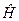для руху частинки в центральноси­мет­рич­ному полі. Отже, системи, які описуються цим оператором Ґамільтона, мо­жуть перебувати в стаціонарних станах одночасно з певним значенням енергії, певним зна­чен­ням квадрата кутового моменту і певним значенням проекції ку­то­вого мо­мен­ту. Хвильові функції цих (стаціонарних) станів одночасно бу­дуть власними функція­ми всіх трьох вище перелічених операторів.

Часова залежність хвильових функцій згаданих стаціонарних станів ха­рактери­зуються множником 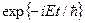, де 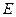– енергія системи. Залежність цих хвильо­вих функцій від кутів 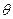і 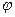теж визначена, а саме, вона цілком визнача­єть­ся значенням 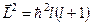і 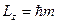, ці функції повинні співпадати з влас­ни­ми функціями 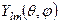операторів 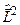і .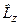

Отже, хвильові функції стаціонарних станів руху частинки з певними зна­чен­нями 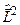і 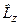в довільному полі сферичної симетрії може бути записано у вигляді

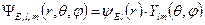. (7.29)

Тут 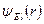– т. з. радіальна хвильова функція. Вигляд цієї функції залежить від 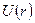, від значень 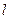. Цей вигляд не залежить від значення магнітного квантового чис­ла 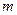, адже у полі сферичної симетрії немає виділених напрямків у просторі.

4) Радіальне рівняння Шредінґера.

Запишемо стаціонарне рівняння Шредінґера для однієї частинки масою m з коорди­натою 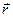у полі центральної сили з потенціальною енергію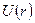

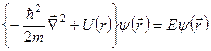. (7.30)

У цьому рівняння внаслідок сферичної симетрії зручно перейти до сферичних коорди­нат .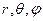

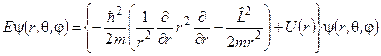. (7.31)

Скористаємось тим, що оператор

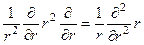. (7.32)

Дійсно,

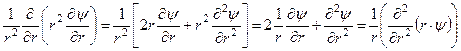. (7.33)

Тепер рівняння Шредінґера запишемо так:

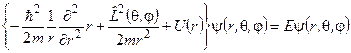. (7.34)

Змінні 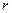та 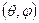у цьому рівнянні розділяються (відокремлюються), і, відповід­но до цього, хвильова функція 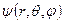зображується як добуток функції 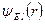, яка залежить тільки від 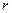, на хвильову функцію 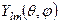, що залежить лише від ку­тових змінних 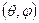і є власною функцією оператора 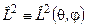та оператора :

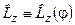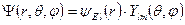. (7.35)

Функцію 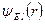, як ми вже казали раніше, має назву радіальної функції. Для цієї функції ми одержуємо рівняння

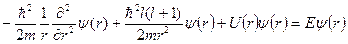. (7.36)

Це рівняння має назву радіального рівняння Шредінґера.

З умови нормування функції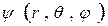

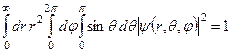(7.37)

та з умови нормування сферичної функції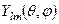

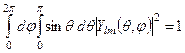(7.38)

одержуємо умову нормування для радіальної хвильової функції :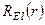

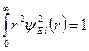. (7.39)

Спеціальні позначення для станів. Стани з різними значеннями орбітального кван­тового числа 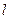позначають спеціальними символами: s -стан відповідає зна­чен­ню ; p -стан – 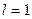; d -стан – 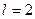; f -стан – 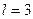. Ці позначення походять від характеристик серій спектральних ліній, що „висвічуються” атомами при їх пере­ходах з цих станів в інші. А саме, символи s, p, d, f – це перші літе­ри англійських слів „ sharp ”, „ principal ”, „ diffuse ”, „ fundamental ”, тобто „різ­ка”, „голов­на”, „розмита”, „фундаментальна” серії.

Дата добавления: 2015-06-04