Лекція 9

Теорія збурень у випадку виродження

У попередній лекції ми розглянули стаціонарну теорію збурень та умови її засто­сування, що зводяться до виконання співвідношення (8.41). Очевидно, що роз­глянута нами теорія не може бути застосована у випадку вироджених рівнів з індексами f і m. Адже у знайдених нами виразах для поправок 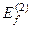і 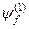підсумовування йде саме за індексами різних станів 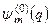, а не за різними значеннями енергії 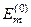. 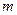У випадку виродженої „нульової” задачі різним станам з індексами і від­повідає одне й те ж значення 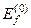. Внаслідок чого у знаменниках знайдених ви­разів для поправок одержимо нулі. Прикладом може служити задача для ато­ма водню, який перебуває у зовнішньому полі. У цьому випадку „нульова” задача – це атом вод­ню без поля. У виразах для поправок підсумовування проводиться за різними станами , тобто за різними індексами станів , , 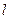, 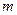а не тільки за . Але енергія 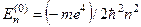не залежить від кван­то­вих чисел 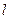і 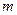. Енергетичні рівні вироджені, і саме це, безумовно, призводить до того, що знайденими формулами у стаціонарній теорії збурень для поправок 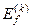та 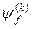користуватись не можна.

Твердження. Збурення 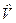може приводити до часткового або до повного знят­тя виродження, тобто енергетичні рівні для збуреної задачі розщеплюють­ся.

Наша задача – знайти розщеплення енергетичних рівнів для збуреної задачі.

Виходимо з рівняння Шредінґера

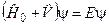. (9.1)

Якщо оператор 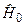має, наприклад, два близькі власні значення 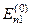і 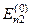, яким відпові­да­ють власні функції і 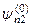, а всі інші власні значення цього оператора 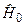„розташовані” далеко від 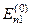, тоді обчислюючи поправки методом теорії збурень ми пере­ко­наємося, що через малість знаменника 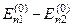вклад власної функції 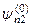буде ве­ликий. Через це доцільно вже у нульовому наближенні шукати розв’язок у вигляді

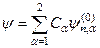. (9.2)

Виявляється, що цією формулою доцільно скористатися і у випадку такої незбуреної системи, енергетичні рівні якої є виродженими, тоб­то, коли рівню енергії 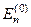відповідає не одна власна функція, а декілька:

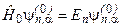, (9.3)

де другий індекс стану 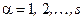, а 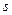– кратність виродження. У цьому випад­ку хвильову функцію 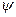доцільно зобразити у вигляді лінійної комбінації з 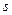функ­цій, що відповідають енергії :

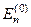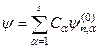. (9.4)

Підставимо тепер вираз (9.4) у рівняння Шредінґера (9.1), потім помножимо цей вираз для рівняння (9.1) на 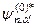і знайдемо рівняння для коефіцієнтів роз­кладу :

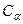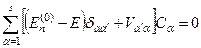, (9.5)

де матричний елемент оператора збурення

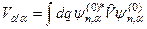, (9.6)

де 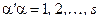. Крім того .

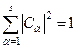Рівняння (9.5) для коефіцієнтів 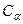має нетривіальний розв’язок, якщо його визнач­ник рівний нулеві:

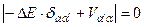, (9.7)

тут введено позначення для шуканого зсуву енергії

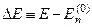, (9.8)

Як приклад, розглянемо випадок двохкратного (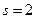) виродження. Для зсуву 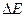у цьому випадку маємо квадратне рівняння

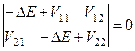, (9.9)

з якого знаходимо

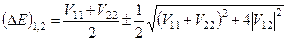. (9.10)

Система рівнянь для коефіцієнтів 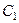і 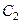матиме такий вигляд:

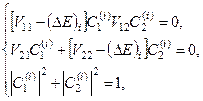(9.11)

.

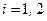З другого рівняння системи (9.11) знаходимо

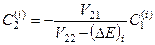. (9.12)

А з третього рівняння системи (9.11) (з використанням формули (9.10)) знаходимо

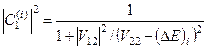. (9.13)

Для спрощення виразу (9.13) допустимо, що 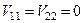. Тоді

, ,

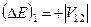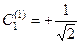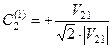, , , . (9.14)

Припущення 1: 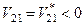. Тоді

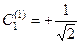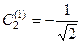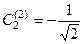, ; , . (9.15)

Ми одержуємо правильні хвильові функції нульового наближення:

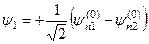, (9.16)

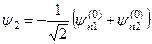. (9.17)

Твердження. Хвильові функці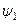ї і 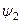ортогональні, а матричний елемент

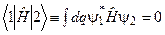. (9.18)

Доведення: 1)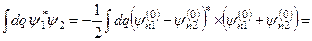

.

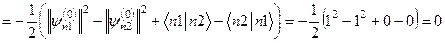2) .

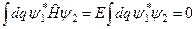Якщо тепер для відшукання поправок до енергії 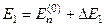(або 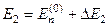) і до хвильової функції 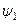(або 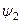) використати знайдені у нульо-вому наближенні енергії

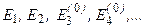
і хвильові функції

,

тоді у знаменниках сум, які виначають енергію у другому наближенні теорії збу­рень

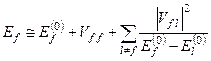(9.19)

і хвильову функцію у першому наближенні

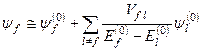(9.20)

(ці два вирази ми отримали у попередній лекції) не буде зустрічатися мала (або рів­на нулеві) різниця 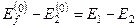. Відсутність у знаменниках згаданих сум цієї різниці зумовлена тим, що чисельник відповідного доданку V ₁₂ рівний ну­лю. Дійсно, функці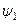ї і 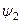– це розв’язки

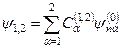(9.21)

рівняння (9.1) з повним Ґамільтоніаном 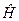. Вище було показано, (9.18), що 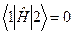. Отже,

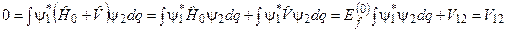. (9.22)

Отже, визначення поправок якого завгодно порядку (наближення) надалі можна зна­хо­дити звичайним методом теорії збурень.

Висновки. Розкриваючи визначник (9.7), одержуємо рівняння степені s від­нос­но невідомого значення Δ E. Це рівняння має s дійсних коренів. Якщо всі корені рівняння (9.7) різні, то s -кратне виродження рівнів 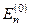незбуреної задачі роз­падається на s різних рівнів E_i, i =1, 2,… s (див. формулу (9.8)). Кожному та­ко­му рівню буде відповідати функція 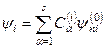. Коефіцієнти 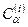цієї функ­ції визначаються із системи рівнянь (9.5) при підстановці замість E значень E_i, i =1, 2,… s. У цьому випадку кажуть, що збурення 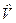повністю знімає вирод­жен­ня. У випадку, коли один або декілька коренів рівняння (9.7) є кратними, ка­жуть, що виродження знято частково. Це яскраво ілюструє т. з. ефект Штар­ка в атомі водню.

Дата добавления: 2015-06-04