Принцип тотожності у квантовій механіці

Системи тотожних частинок

Всі основні принципи, постулати та рівняння квантової теорії мають місце у квантовій механіці незалежно від того, розглядається кван­то­ва система, що складається з однієї частинки, чи з сукупності частинок. Але при розгляді багаточастинкових квантових систем однакових (тотожних) частинок – систе­ми додатково виявляють деякі специфічні особливості прин­ци­пового характер­у, які не мають аналога у класичній механіці. Які це тотожні частинки? Це частинки, що мають однакову масу, заряд, спін та всі інші характеристики, а також поводяться однаково в тих самих умо­вах, полях. Чи можна в принципі простежити за окремою такою частин­кою системи, чи можна розрізнити тотожні частинки? У класичній меха­ні­ці за класичними частинками можна простежити та розрізнити їх. Адже класич­ні частинки рухаються кожна по своїй траєкторії. Через це вони не втра­ча­ють своєї індивідуальності.

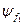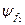У квантовій механіці все по-іншому. Адже тут поняття траєкторії не має змісту. Че­рез це у квантовій механіці немає жодної змоги розрізнити тотожні частинки. Щоб наочно переконатися у цьому, ми розглянемо квантову систему з двох невзаємо­діючих між собою тотожних частинок. Позначимо через і хвильові функці, що описують фізичні стани цих частинок. Тут 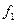і 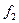– різні набо­ри квантових чисел, які ідентифікують фізичні стани. Через 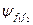познача­ти­мемо хвильову функцію системи двох наших частинок. Зобразимо схематич­но на площині (див. рис. 1) носі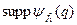ї*⁾ і 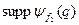. Нехай у початковий мо­мент часу 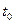ці носії локалізовані кожний у своїй області, які не перекривають­ся.

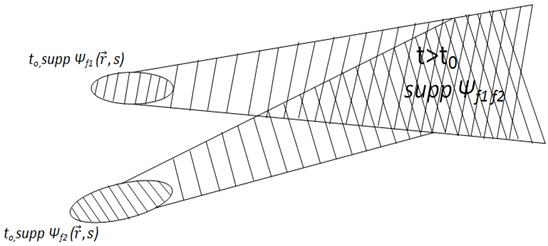
Рис. 1. Носії хвильових функцій у початковий момент часу 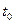і у момент .

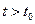Але у наступні моменти часу 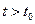два носії хвильових функцій 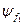і 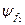«роз­пли­ваються» і можуть вже перекриватися. Отже, «виловивши» частинку в мо­мент 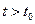, коли має місце перекривання носіїв і нумерація частинок внаслі­док цього переплутується, ми не зможемо ідентифікувати, яку з двох то­тож­них частинок «виловлено». Як наслідок тотожності частинок, розподіли 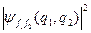і 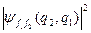співпадають, тобто, виконується рівність: для всіх , ,

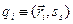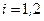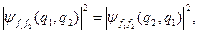
що і є математичним формулюванням так званого принципу тотожності части­нок. Тут 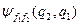є хвильовою функцією системи двох тотожних частинок після переста­новки цих частинок місцями. Звідси випливає, що хвильова функція 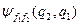систе­ми двох тотожних частинок з точністю до фазового множника 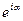збігається з вихід­ною функцією :

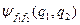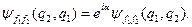
Знайдемо значення фази 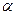. Введемо оператор перестановки частинок 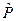такий, що

Отже,

є рівняння на власні значення та власні функції оператора 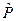. Подіємо на це рівняння ще раз оператором :

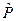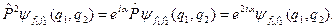
З іншого боку

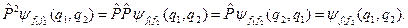
Отже виходить, що

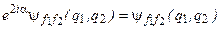
або

, ,

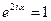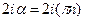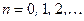
Тобто 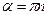, а власне значення оператора 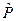є

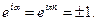
Таким чином, остаточно,

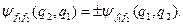
Висновок. Після перестановки двох тотожних частинок хвильова функція двочастинкової систе­ми може змінювати тільки знак. Зауважимо, що позна­чен­ням 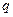у аргументі хвильової функції виражена її залежність як від просторо­вих 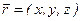, так і від спінових координат: .

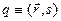Результат. При перестановці будь-яких двох частинок у сукупності 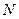то­тожних частинок хвильова функція або не змінює знак, або змі­нює його на протилежний. Отже, хвильова функція системи тотожних частинок є або симетричною, або антисиметричною.

Твердження. 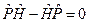, де 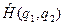– Ґамільтоніан системи двох тотожних частинок.

Доведення. У квантовій механіці Шредінґера 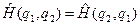. Отже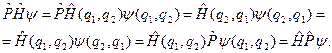

Висновок. Оператор перестановки 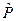комутує з Ґамільтоніаном і, отже, він є інтегралом руху. Властивість 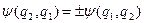зберігається з часом!

Дата добавления: 2015-06-04