Лекція 13

Парагелій, ортогелій

Продовжимо розгляд атома гелію в Шредінґерівський (нерелятивістській) кван­товій механіці. Ми уже знаємо, що спінові змінні в стаціонарному рівнянні Шре­дінґера розділяються, а розв’язки можна записати як добуток координатної частини на спінову

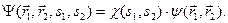
Електрони – це ферміони, тому повинна виконуватись загальна вимога анти­симет­рії повної хвильової функції системи двох електронів:

Тут, і надалі, сукупність трьох просторових змінних 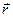та спінову змінну 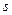ми позна­ча­тимемо як , а символами «» та «» буде відображатись відповід­но симетричність та антисиметричність тих хвильових функцій, які у нижніх індексах мають ці символи. У зв’язку з вищезгаданою вимогою антисиметрії можливі два класи станів атома гелію:

Розглянемо спочатку побудову спінових функцій та . Оскільки спіно­ві взаємодії в розглядуваному нами випадку нерелятивістської квантової меха­ніки не входять в Ґамільтоніан атома гелію, спінові змінні та теж роз­ді­ляються:

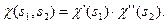
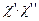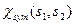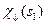Отже, зі всіх можливих щойно записаних добутків ми маємо утворити спіно­ві функції та . Для того, щоб реалізувати цей намір, ми зга­даємо чотири одноелектронні (власні) спінові функції: , , , . З цих чотирьох функцій можна утворити комбінації, які володіють пев­ною симетрією. Очевидно, що для побудови антисиметричної спінової функції є тільки одна можливість

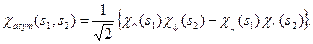
Ми вже дослідили на минулій лекції спіновий стан системи двох електронів, що описується функцією , і знаємо, що повний спін системи двох електронів у цьому випадку дорівнює нулеві. Ще раз підкреслимо - у цьому випадку маємо систему двох електронів із протилежно направленими спі­нами. Ми також знаємо, що це синглетні стани.

Ми вже знайомі з одним із таких станів, це – основний стан атома гелію, коли хвильова функція стану в нульовому наближенні теорії збурень має вигляд

де

, ,

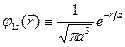Повна енергія основного стану у першому наближенні теорії збурень

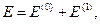
де

а поправка

Ми скористалися тим, що спінова функція нормована:

Завдання для практичного заняття. Довести, що

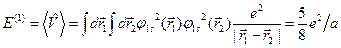. Отже, повна енергія основного стану атома гелію в першому наближенні теорії збурень

,

Є безліч збуджених станів атома гелію, у яких система двох електронів має протилежно направлені спіни. Легко здогадатися, як слід (за допомогою одно­електрон­них спінових та будь-яких двох різних одноелектронних коорди­натних хвильових функцій) будувати нульове наближеня повних хвильових функцій цих збуджених станів атома гелію. Так, наприклад, нульове набли­ження симетричної координатної хвильової функції найнижчого збудже­но­го стану з електронною конфігурацією , тобто, коли один з електронів перебуває у -стані, а другий – у -стані, матиме вигляд

Тут 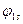та – одноелектронні координатні хвильові функції відповідно та стану. Звичайно, що спіновий стан у розглядуваному випадку буде опису­ва­тися антисиметричним спінором . Основний стан і всі подібні збуджені стани з протилежно направленими спінами системи двох електронів, тоб­то стани з симетричною координатною частиною повної хвильової функції , мають назву пара-станів.

Але поряд з пара-станами є безліч станів атома гелію з антисиметричною координат­ною частиною хвильової функції. Про ці стани ми говоримо, коли реалі­зується другий з двох можливих випадків, тобто, коли повна хвильова функція належить до другого класу, а отже має вигляд

У другому випадку завжди при вибраній антисиметричній коорди­натній функції 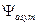симетричну спінову функцію можна утворити вже не одним, а трьома способами:

Відповідно до цього у нас з’являються три типи станів другого класу, а саме: , .

Завдання для практичних занять

Завдання 1. Знайти результат дії оператора проекції на вісь 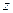повного спіну (оператора ) на спінові функції , , і довести, що

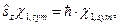
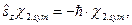
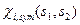Завдання 2. Знайти результат дії оператора квадрата повного спіну на спінові функції , і довести, що

,

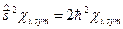Висновки

1. Спінові стани , – це власні стани оператора квадрата повного спіну системи двох електронів атома гелію з власним значен­ням рівним 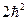. Отже, 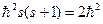, тобто спін . Таким чином, спіно­ві хвильові функції , описують стан системи двох електронів зі спіном рівним одиниці.

2. Число спінових станів системи дорівнює . Отже, маємо триплет­ний стан. Оскільки в окремому триплеті повні хвильові функції (тобто функції: , ) від­різ­няються тільки спіновими частинами (бо в даному триплеті коорди­натна частина повної хвильової фунції одна й та сама), енергія атома гелію однакова у всіх трьох станах даного триплету.

3. Антисиметричні координатні частини повних хвильових функцій різ­них триплетів утворюємо завжди за відомим „рецептом” з окремої пари двох різних одноелектронних координатних хвильових функцій. Наприклад, найнижчий збуджений стан з електронною конфігурацією антисиметрична координатна частина повної хвильової функції має вигляд:

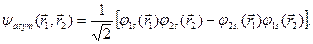
4. Будемо називати триплетні стани системи двох електронів, у якої, як бачимо, спін рівний одиниці, ортостанами. Зауважимо, що спінові функції , , триплетних станів та спінова функція синглет­них станів ортонормовані, тобто три скалярні добутки , , рівні нулеві. У цьому легко переконатися. Наприклад,

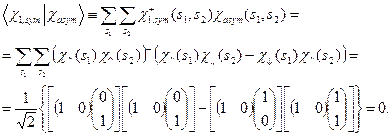
Внаслідок ортогональності спінових функцій триплетних та синглетних станів атома гелію, матричні елементи переходів між пара- і ортостанами атома гелію будуть рівні нулеві. Адже внаслідок того, що у рамках нерелятивістсь­ко­го наближеня спінові і просторові змінні хвильових функцій відокремлюють­ся, скалярні добутки

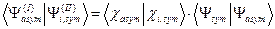
для рівні нулеві. Отже, у цьому наближенні переходи між парастанами і орто­станами атома гелію є забороненими. Тому, якщо «закинути» атом гелію в триплет­ний стан, то він (внаслідок випромінювання або поглинання фотона) ніколи не зможе перейти у синглетний стан. Можна сказати, що ми маємо два сор­ти атомів гелію. Якщо спіни електронів в атомі гелію є антипаралельними (синглетний стан!), тоді його називаємо парагелієм. Атом гелію у триплетному стані має назву ортогелія.

Дата добавления: 2015-06-04