Лекція 14

Релятивістська квантова механіка

Рівняння Клейна-Гордона-Фока

Рівняння Шредінґера

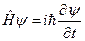
не описує релятивістських ефектів, коли швидкості частинок великі й сумірні зі швид­кістю світла (). Воно також не задовольняє вимоги теорії відносності Ейнштейна, адже просторові координати 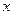, , 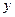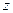і часова змінна 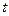входять у це рів­няння несиметрично, в той час як у релятивістській теорії ці змінні є рівно­правні. Важливо встановити таке рівняння, яке б задовольняло як вимоги теорії відносності, так і основні принципи квантової теорії.

Як можна забезпечити потрібну симетрію входження часу і просторових координат у рівняння руху і тим самим задовольнити основні принципи реля­ти­вістської квантової механіки? Слід звернутись до виразу для функції Ґа­мільтона 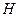у релятивістській механіці:

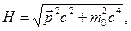
де , , 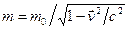– маса спокою частинки. Бажану симетрію можна створити, якщо виходити з квадрата енергії 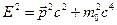та одночас­но виконати тут формальну заміну імпульсу 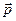на оператор 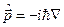, а енергію 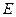– на похідну 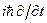. Після цього одержується таке рів­нян­ня для хвильової функції :

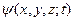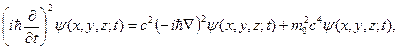
або

Таким чином, отримано відоме рівняння Клейна-Гордона-Фока. У це рівнян­ня входить друга похідна за часом та другі похідні за координатами. Рівняння Клейна-Гордона-Фока (К-Г-Ф) є релятивістськи інваріантним.

Щоб дослідити на основі рівняння К-Г-Ф рух електрона у електромагніт­но­му полі, нам слід познайомитися з процедурою «вмикання» поля з потен­ціалами і 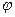у квантовій механіці*⁾. У відповідності з цією процедурою роби­мо такі зсуви операторів:

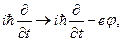
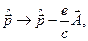
і рівняння К-Г-Ф для електрона в полі набуває вигляду:

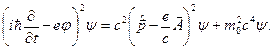
Стаціонарне рівняння К-Г-Ф.

Це рівняння одержуємо, якщо потенціали 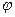і не залежать від часу. Змін­н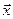і і 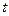у цьому випадку відокремлюються, хвильова функція 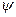представ­ля­ється у виляді

координатна частина хвильової функції задовольняє рівняння

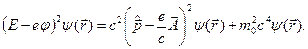
Це і є стаціонарне рівняння К-Г-Ф.

Рівняння К-Г-Ф для атома водню.

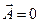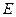У цьому випадку , . Крім того, енергію будемо відраховувати від енергії спокою:

Тоді рівняння К-Г-Ф запишемо так:

Твердження. Точне рівняння К-Г-Ф для атома водню можна записати у вигляді:

де оператор співпадає з оператором Ґамільтона для атома водню в нереля­тивістській квантовій механіці, тобто

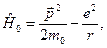
оператор 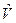має вигляд

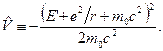
Щоб довести справедливість цього твердження, досить розкрити квадрат , тобто записати вираз

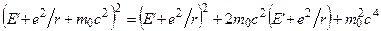
і підставити його у рівняння К-Г-Ф для атома водню.

Наголосимо, що рівняння К-Г-Ф для атома водню у всіх підручниках з кван­тової механіки розв’язано точно. У наших лекціях на цьому спеціально зупи­нятись не будемо. Однак зауважимо, що у нерелятивістському наближенні оператор

Це означає, що у так званому квазірелятивістському наближенні, коли 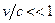, опе­ратор 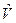може грати роль оператора невеликого збурення, так що можна користу­ва­тися методом теорії збурень. Тоді Ґамільтоніа­ном нульової задачі

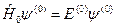
буде оператор

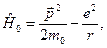
а оператором збурення буде оператор

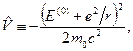
де

,

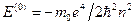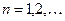
У першому наближенні за теорією збурень енергія

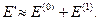
Першу поправку 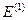визначає діагональний матричний елемент оператора збу­рення, розрахований на хвильових функціях нерелятивістського атома водню:

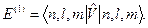
Завдання для практичних занять

Довести, що релятивістська поправка 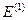до енергії залежить від квантового числа 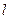та рівна

де 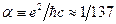– стала тонкої структури.

Висновки:

1. Повна енергія 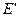залежить від квантового числа 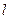та в цьому наближенні

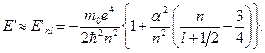
2. У теорії К-Г-Ф виродження енергетичних рівнів за 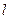знімається, тому систе­му рівнів енергії при заданому головному квантовому числі мають назву тонкої структури енергетичного спектра (це є дуже цікавий результат!).

Тепер коротко торкнемося питання узгодження одержаної формули для з експериментом. Повного узгодження немає! Є тільки якісне узгоджен­ня. Це пов’язано з тим, що рівняння К-Г-Ф описує частинки з нульовим спіном. Це рівняння не враховує спін електрона, який, як ми вже знаємо, рівний .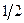

Згадане узгодження буде мати місце, якщо врахувати наявність у електро­на спіну. Але цього не мо­же досягти теорія К-Г-Ф, а тільки – теорія Дірака. Зокрема, в теорії Дірака для атома водню одержуємо

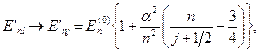
де 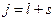– квантове число квадрата повного момента кількості руху електрона із . Тепер одержаний результат для енергії 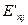добре узгоджується з екс­пе­риментально виміряними значеннями, на відміну від формули теорії К-Г-Ф.

Дата добавления: 2015-06-04