Спін основного стану атома гелію

Атом гелію є найпростішим серед багатоелектронних атомів. Це система двох електронів, що рухаються у полі ядра із зарядом 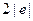(див. рис. 1).

**

У запропонованій моделі атома гелію будемо вважати ядро нерухомим, адже від­ношення маси 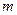електрона до маси 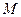ядра є малою величиною, . Помісти­мо ядро у початок координат. Ґамільтоніан такої системи є

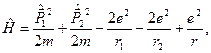
де 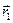, 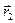– радус-вектори електронів, 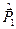, 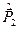– оператори їхніх імпульсів, а 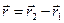. Електрони – це ферміони, і повна хвильова функція 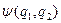, , , 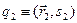повинна бути антисиметрична:

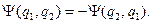
Спінові та просторові координати розділяються:

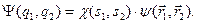
Ми позначимо оператор енергії міжелектронної взаємодії через 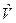, тобто . На першому етапі досліджень атома гелію доцільно застосовувати ме­тод теорії збурень, де у ролі оператора збурень 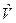вибрано оператор енергії між­електрон­­ної взаємодії.

З такої точки зору ми розглянемо основний стан атома гелію, тобто основ­ний стан системи двох електронів, які не взаємодіють між собою, а взаємо­діють тільки з «нерухомим» ядром. Що є «нульове наближення для основного стану атома гелію»? Це стан двох електронів, що задається кванто­ви­­ми числами: 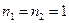, , . Кожен електрон цього стану перебуває у -стані. За допомогою двох одноелектронних функцій 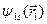і можна утво­ри­ти лише симетричну координатну хвильову функцію 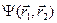, тобто

де

,

.

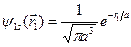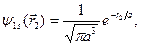
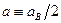Таким чином, спінова функція 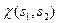системи двох електронів у згаданому основному стані повинна бути антисиметричною. Як слід будувати цю функ­цію? Її слід утворити з таких одноелектронних спінових функцій, з якими ми познайомилися у Лекції № 11:

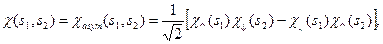
де одноелектронні спінові функції мають вигляд

,

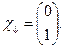
Змінною 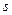тут слугує проекція спіну на виділену вісь. Ця змінна набуває два значення .

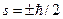Задача. Дослідити спіновий стан системи двох електронів, який описує спінова хвильова функція , що описана вище.

Твердження 1. Функція є власною функцією оператора 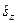проек­ції повного спіну на вісь 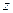системи двох електронів з власним значен­ням рівним нулю. Тут

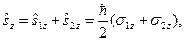
, – оператори спінів першого та другого електронів.

Доведення.

Врахуємо, що

,

,

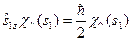Після підстановки останніх чотирьох рівностей у вираз для 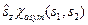одержуємо:

Висновок. Спінова функція є власною функцією оператора проек­ції повного спіну на вісь 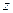із власним значенням рівним нулеві.

Завдання для практичного заняття. Довести, що спінова функція є власною функцією оператора квадрата повного спіна

системи двох електронів, яка відповідає власному значенню рівному нулеві, тобто

Висновок. Функція є власною спіновою функцією оператора квадрата повного спіну та його проекції з власними значеннями, рівними нуле­ві. Але власне значення квадрата оператора спіну дорівнює 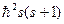. Отже, у на­шому випадку , тобто 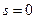. Це означає, що повний спін системи двох електронів у стані з спіновою функцією дорівнює нулеві. У цьому випадку маємо систему двох електронів з протилежно направле­ни­ми спінами. Число спінових станів є 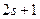. У нашому випадку 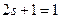. Це дає можли­вість сформулювати остаточний результат: основний стан атома гелію є синглетний стан з нульовим спіном.

Дата добавления: 2015-06-04