Лекція 11

Спін електрона

Йдеться про власний механічний момент електрона або, як кажуть, про спін електрона. Досі ми розглядали хвильову функцію квантової частинки (зо­крема електрона) як комплекснозначну функцію лише просторових змінних 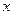, , 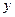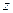і часу 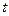. Просторові змінні хвильової функції часто називаємо зовнішні­ми змінними. Електрон має три зовнішні ступені віль­ності і з ними пов’язана наявність у електрона орбітального момента кількості руху. Адже момент імпульса електрона зумовлений саме його просторовими переміщеннями як цілого. Чи вичерпується повний механічний момент кількос­ті руху електрона тільки його орбітальним моментом? Ні. У хвильової функції електрона, крім зовнішніх, є ще й внутрішні змінні, які описують його внутрішні ступені віль­ності. Слід говорити не тільки про орбітальний момент кількості руху електро­на, а й про його власний механічний момент кількості руху, тобто про спін електрона.

Ми уже знаємо, що у нерелятивістській квантовій механіці орбітальний мо­мент кількості руху є інтегралом руху для вільного електрона з Ґаміль­тоніаном 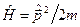. Адже у цьому випадку комутатор

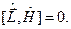
Однак, у релятивістській квантовій механіці, до вивчення якої ми скоро приступимо, поєднання у рівнянні Дірака для вільного електрона фундамен­тальних принципів квантової механіки і теорії відносності породжує ще і додаткові, як побачимо згодом, аж ніяк не тривіальні внутрішні ступені вільності, і внаслі­док цього проекції орбітального момента кількості руху вільної частинки (електрона) вже не є інтегралами руху. Інтегралом руху у теорії Дірака є повний механічний момент кількості руху електрона, який виражається через суму двох операторів:

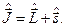
Щоб з’ясувати зміст оператора 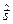у записаній щойно сумі, ми розглянемо електрон у системі координат, де він як ціле не рухається («сядемо» на елект­рон), тобто його імпульс у цій системі координат, а також момент імпульсу, дорівнює нулеві. У такій системі координат електрон матиме лише «внутріш­ній» (власний) механічний момент кількості руху, тобто спін.

Легко здогадатися, якою повинна бути алгебра трьох операторів 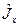, , 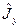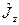. Очевидно, що вона повинна бути такою, як і алгебра операторів 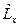, , 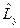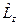. Отже, приймається, що трійку операторів 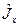, , 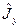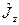характеризує така алгебра:

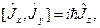
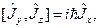
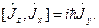
Цим ми вводимо до розгляду і алгебру трьох операторів , , :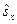

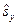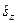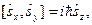
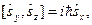
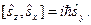
З теорії Дірака випливає, що оператор

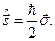
Тут

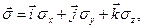
де три матриці Паулі

, , .

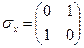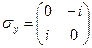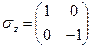Це легко зрозуміти, якщо розглядати наведену вище алгебру операторів 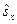, , 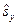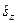як три операторні рівняння для знаходження трьох проекцій оператора спіна 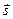. Легко переконатись, що оператор 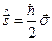задовольняє ці три операторні рівняння. Для цього слід спочатку переконатись, що з явного вигляду трьох матриць Паулі випливає

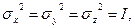
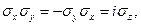
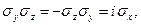
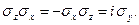
Тепер домовимося про позначення. Приймемо, що 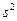– це власне значення квадрата власного момента кількості руху електрона 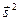. Його будемо нумерувати квантовим числом 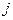, яке є аналогом знайомого нам квантового числа 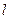. Отже, 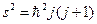. Але квадрат оператора спіну 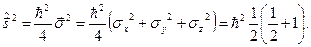Звідси випливає, що власне значення квадрата власного моменту кількості руху електрона, тобто спіна електрона, визначається квантовим числом 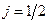. Або іншими словами, спін електрона дорівнює .

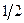Далі, власні значення оператора 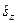позначимо через 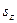. Його будемо нумерувати квантовим числом 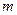. Нагадаємо, що оператори 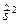і 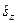комутують, отже вони мають спільну множину власних функцій, яку позначи­мо як 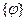. Будемо позначати власні стани також і символами 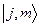. У цих позначеннях рівняння на власні значення 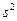і 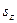та власні стани операторів 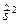і 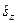мають вигляд:

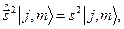
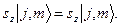
Знайдемо власні стани, або іншими словами власні функції, оператора 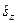(а отже і оператора 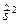). Для зручності запишемо друге з щойно згаданих рівнянь у вигляді

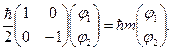
У цій формулі шуканий власний стан 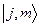позначено матрицею, що має вигляд стовпця

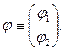
Як бачимо, оператори 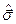«діють» у лінійному просторі дво­рядних матриць-стовпців. Є тільки два розв’язки вищезгаданої задачі, а саме:

1) ,

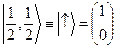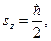
2) ,

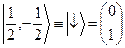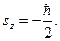
Спінові функції 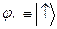, 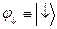утворюють повну (замкнену) систему власних ста­нів оператора .

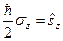Зробимо тепер декілька важливих зауважень. По-перше, „таїнство” меха­нізм форму­ван­ня власного моменту кількості руху елементарних частинок невідомий. Р. Кроніг спробував розглядати спін електрона як обертання твердого тіла (дзи­ги) навколо осі, але скоро він сам відкинув нав’язувати цю або якусь іншу меха­ніч­ну модель. Адже легко безпосереднім обчисленням переконатися, що ліній­на швидкість обертання поверхні у запропонованої Кронігом «електрона-дзи­ги» буде більша, ніж швидкість світла. Вважається, що спін елементарної час­тин­ки є такою же властивістю, як, наприклад, її заряд, чи її маса. Своє послідов­не пояснення спін електрона знаходить у релятивістській квантовій теорії Дірака.

Про частинки з квантовим числом 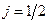говорять, що їх спін чисельно рівний од­ній другій. Прикладом таких елементарних частинок є електрон, протон, нейт­рон, мюон, нейтрино, тощо. Є елементарні частинки з квантовим числом 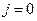, тобто є частинки з «нульовим спіном» – це мезони. Фотон має спін рівний одиниці. Взагалі є елементарні частинки як з цілим, так і з напівцілим спіном.

По-друге, у сьогоднішній лекції ми запровадили «внутрішні» змінні у хвильових функцій. Важливо зауважити при цьому, що у нерелятивістській квантовій механіці, тобто у квантовій механіці Шредінґера, яку ми зараз вивчаємо, Ґамільтоніани квантових систем не залежать від цих «внутрішніх» (спінових) ступенів вільності. Через це рівняння Шредінґера допускає розді­лення (відокремлення) спінових і просторових змінних. Отже, у нерелятивістсь­кій квантовій механіці, коли Ґамільтоніан 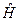не залежить від спінових змінних, хвильова функція 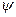як функція просторових координат 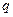і спінових змінних 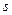завжди представляються у вигляді добутку

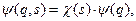
де 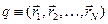, , 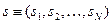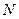– число частинок системи. Функція 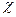, яка зале­жить лише від спінових змінних, має назву спінової хвильової функції, а функція 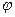, яка залежить лише від просторових змінних, це координат­на хвильова функція.

Дата добавления: 2015-06-04