Лекція 5

Властивості власних функцій і власних значень самоспряжених операторів з дискретним спектром

Нехай спектр оператора , який відповідає фізичній величині F, має дискретний характер і повністю вичерпується тільки невиродженими власними значеннями F_n, n =1,2,… Сформулюємо деякі властивості власних значень F_n і власних функцій ψ_n цього оператора у вигляді таких трьох тверджень:

Твердження 1. Власні значення ермітових операторів є дійсними, F_n = F_n ^*.

Твердження 2. Власні функції ермітового оператора утворюють систему ортонормованих функцій, тобто задовольняють умові

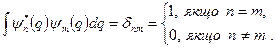(5.1)

Твердження 3. Множина всіх власних функцій ермітового оператора 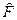утворює повну (замкнену) систему функцій*⁾. Це означає, що будь-яка інша функція 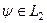може бути представлена у вигляді ряду

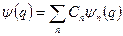, (5.2)

де сумування поширюється на всі значення квантового числа n.

Останнє твердження означає, що довільну функцію 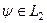можна розкласти в ряд за власними функціями ермітового оператора. Легко визначити спосіб обчислення коефіцієнтів такого розкладу:

, (5.3)

отже, коефіцієнт розкладу

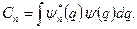(5.4)

Покажемо, що квадрат модуля коефіцієнта C_n у розкладі хвильової функції 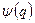в ряд за власними функціями ермітового оператора 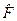визначає імовірність того, що в результаті вимірювання фізичної величини F у стані 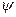ми одержимо значення F_n. Дійсно, середнє значення < F > величини F у стані 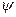співпадає (згідно з аксіомою) зі значенням, яке отримується зі співвідношення

. (5.5)

Користуючись властивістю повноти системи власних функцій оператора 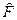, можна представити 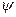у вигляді лінійної комбінації

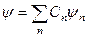. (5.6)

Крім того, скористуємося також рівнянням

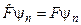(5.7)

і умовою ортонормованості системи функцій 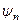. В результаті одержимо:

.

Отже,

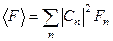. (5.8)

Покажемо також, що умова нормування хвильової функції і властивість повно­ти власних функцій приводять до рівності

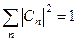, (5.9)

яка має назву „ умова повноти”.

Дійсно,

.

Рівність (5.8) та умова повноти (5.9) дозволяють стверджувати, що квадрат мо­ду­ля коефіцієнта C_n дорівнює імовірності реалізації стану 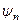, тобто C_n ви­значає міру участі стану 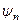у формуванні стану .

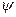Доведення справедливості Тверджень 1 і 2 прості, вони приведені нижче, в Додатку. Твердження 3 ми приймемо без доведення.

Зауваження. Що стосується власних функцій ψ_F операторів 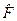, які мають тільки неперервний спектр власних значень F, то вся їх множина теж утворює повну систему функцій, тобто будь-яку функцію 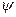можна представити у вигля­ді суперпозиції власних станів ψ_F. У зв’язку з неперервним характером спектра власних значень, така суперпозиція записується не у вигляді суми, а у вигляді інтеграла

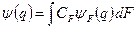, (5.10)

а коефіцієнти розкладу (коефіцієнти суперпозиції)

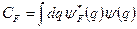. (5.11)

Величина 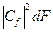визначає імовірність того, що у стані фізична величина має значення, що лежить в інтервалі (F, F + dF).

Приклад. Розглянемо множину хвильових функцій вільної частинки, що ру­хається у необмеженому об’ємі з довільно фіксованими можливими значення­ми імпульсу. Для одновимірного випадку оператор імпульсу має вигляд 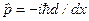, а множиною власних функцій цього оператора є „континуальна” множина плоских хвиль де Бройля

. (5.12)

Власні функції залежать від p як від параметра, який пробігає неперервну множину значень від –∞ до +∞. Сукупність усіх функцій утворює повну (замкнену) систему функцій, тобто будь-яка функція 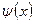може бути представ­лена у вигляді лінійної суперпозиції станів 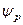, у яких імпульс p частинки має певне значення:

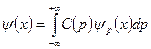, (5.13)

. (5.14)

Величина 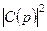– густина імовірності того, що частинка має імпульс в око­лі значення p. У тексті Лекції 3, формула (3.23), ми ввели тривимірний інтегральний розклад Фур’є функції , а саме: у зв’язку з повнотою систе­ми функцій 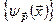, , 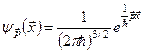для „будь-якої” функції 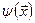існує інтегральний розклад Фур’є

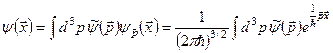. (5.14)

У цьому розкладі коефіцієнти 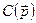позначені як 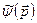. Функція 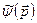є хви­льовою функцією у p -зображенні. Для неї слід писати інтегральний розклад

, (5.15)

який є т. з. оберненим перетворенням Фур’є. Величина 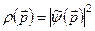– це густи­на імовірності повних значень імпульсу частинки у стані .

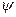Дата добавления: 2015-06-04