Основні поняття

Розпочнемо з розгляду двох важливих питань. Перше – це питання про спо­соби задання станів фізичних об’єктів у класичній фізиці. Друге – про закони зміни станів, тобто, – про класичні рівняння руху у фізиці. З курсу класичної механіки відомо, що задання стану класичної механічної системи у деякий мо­мент часу t, означає одночасне задавання точних значень узагальнених коорди­нат q_α і узагальнених імпульсів p_α (α =1, 2,…, s, де s – число ступенів вільності розглядуваної механічної системи) у цей момент часу. Щоб задати закон зміни стану механічної системи в часі, потрібно скласти відомі рівняння руху, наприклад, у формі Ґамільтона:

, , (α =1, 2,…, s). (1.1)

Для вільної класичної частинки задавання її фізичного стану у деякий мо­мент часу означає задавання у цей момент часу точних значень трьох коорди­нат (x, y, z) і трьох проекцій імпульсу (p_x, p_y, p_z) цієї частки, а рівняннями руху є рівняння Ньютона.

Підкреслимо, що вищезгаданий спосіб задавання фізичного стану „класич­ної частинки”, а також спосіб задавання рівняння руху мовчазно допускає апрі­орну притаманність „класичної частки” мати одночасно точне значення поло­ження (x, y, z) і точне значення імпульсу (p_x, p_y, p_z). У класичній механіці неявно допускають, що: 1) закон руху класичної частинки (тобто векторнозначна функ­ція 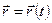) є неперервною функцією часу; 2) класична частинка здійснює рух за траєкторією; 3) дотична до траєкторії руху вільної класичної частинки існує у будь-якій її точці, – а отже, точні значення як положення 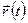, так і імпульсу 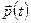одночасно існують. Це й спричинило можливість задавання фізичного ста­ну механічної системи, її рівняння руху, вищезгаданим чином. Добре відомо, що ці апріорні допущення класичної механіки блискуче підтверджені всіма кла­сичними дослідами з вивчення механічного руху.

Мета даної лекції полягає в знаходженні відповіді на питання про спосіб за­давання фізичного стану мікрочастинки (наприклад, електрона, фотона) у кван­товій механіці, а в наступних лекціях нам слід розв’язати питання про вигляд рівняння руху у квантовій механіці. Пошуки відповідей на ці два фундамен­тальні питання складають історію створення за дуже короткий час
(1923-1927рр.) сучасної квантової теорії, – нерелятивістської і релятивістської квантової механіки, а також створення дещо пізніше релятивістської теорії квантованих полів. За браком часу ми не будемо вдаватися до розгляду питань історії розвитку фізичних ідей, що призвели до феномену створення сучасної квантової фізики – унікального явища, якому важко відшукати прецедент в історії розвитку науки (детальніше див. [1]).

Коротко окреслимо першу спробу, яка природним чином і дуже послідовно може підвести нас до розв’язання поставлених вище фундаментальних проблем. Поста­вимо питання таким чином: чи можна безпосередньо поширити вищезгадані апріорні припущення класичної механіки на випадок мікрочастинки, скажімо, коли ми маємо справу з електроном, чи фотоном? Очевидно, що відповідь на це питання може дати тільки експеримент. Це, зокрема, – відомі дифракційні та інтерференційні досліди з т. з. „поодинокими” електронами.

Виявляється, не тільки ансамблю електронів, а й кожному окремому елект­рону притаманні „дивні” властивості, які проявляються під час проходження „поодинокого” електрона через систему двох щілин в екрані. Це „примушує” нас заново поставити питання про статус таких „запозичених” із класичної ме­ханіки фізичних величин як положення мікрочастинки та імпульс мікрочастин­ки. Нижче буде показано, що одночасні точні значення положення та імпульсу мікрочастинки раз і назавжди втрачають статус фізичних величин і через це потрібно відмовитися від класичного способу задавання фізичного стану мікро­частинки. Натомість потрібно запропонувати інший, експериментально під­тверджений і фізично осмислений спосіб задавання стану фізичної системи у квантовій механіці. Очевидно, що іншим чином повинно записуватися також і рівняння руху. Потрібно також проаналізувати способи задавання фізичних ста­нів та рівнянь руху у класичній електродинаміці та класичній теорії гравітації.

Для визначення фізичного стану електромагнітного поля, слід задати зразу чотири функції координат простору x, y, z і часу t. Це т. з. скалярний потенціал і векторний потенціал 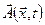. Ці чотири функції зв’язані зі експериментально спостережува­ними силовими характеристиками електро­маг­нітного поля 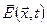та добре відомими співвідношеннями – а саме, двома рівнянями Максвелла: , 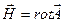. Тепер, щоб задати всі рівнян­ня руху електромагнітного поля – озна­чає записати відомі рівняння Максвелла для величин та 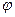. Ці рівняння, як і рівняння Ньютона в механіці, є вихідними.

При побудові апарату квантової механіки ми не будемо апелювати до теорії гравітаційного поля. Стан цього поля, як добре відомо, описується метричним тензором, який залежить від чотирьох криволінійних координат, а рівняння руху гравітаційного поля є т. з. рівнянням Ейнштейна-Ґільберта.

Аналіз експериментальних даних з вищезгаданих дифракційних та інтер­ференційних дослідів свідчить, що спосіб задавання фізичного стану в класич­ній електродинаміці теж не є придатним для квантово-механічних систем. Для розв’язання корінного питання про спосіб задавання фізичного стану мікро­об’єкта чи будь-якої іншої квантово-механічної системи, була прийнята основ­на аксіома квантової механіки: стан квантової фізичної системи задається хвильовою функцією Ψ. Поняття хвильової функції Ψ є фундаменталь­ним у рамках квантової механіки. Функція Ψ є комплексно-значною функцією просторових координат і часу. Наступною аксіомою, яка стосується рівняння руху в квантовій механіці, є т. з. рівняння Шредінґера, якому повинна задоволь­няти функція Ψ. Підкреслимо, що обидві згадані аксіоми спираються на результати численних унікальних експериментів з квантовими системами і, в свою чергу, є узагальненням даних цих експериментів.

Для квантової частинки маси m, яка рухається у полі з потенціалом U(x, y, z), хвильова функція Ψ залежить від просторових координат x, y, z і часу t. Рівняння руху для хвильової функції Ψ (x, y, z, t) у цьому випадку вперше записав Е. Шредінґер (1926р.) у вигляді

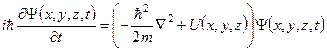. (1.2)

Тут , де h – стала Планка. Величина є однією з фундаментальних фізичних констант, що має розмірність дії і є елементарним квантом дії. Наближено вона рівна 1.05∙10^–27 ерг∙сек.

Дата добавления: 2015-06-04